B: 数学基础知识
- Page ID
- 200345
正方形和其他权力
指数或幂是重复乘法的数学简写。 例如,指数 “2” 表示将该指数的底数乘以其本身(在此示例中,基数为 “5”):
\[5^2=5×5=25\]
指数是 “2”,基数是数字 “5”。 这个表达式(将一个数字乘以本身)也称为正方形。 任何提高到 2 次方数的数字均为平方。 任何提高到 3 次方数的数字都会被立方体:
\[5^3=5×5×5=125\]
提高到第四次幂的数字等于该数字自身乘以四倍,以此类推,获得更高的幂次方。 一般来说:
\[n^x=n×n^{x−1}\]
计算百分比
百分比是一种使用分成 100 个部分的整数来表示某物的分数量的方法。 百分比是分母为 100 的比率。 我们使用百分比符号% 来显示百分比。 因此,25% 表示比率为\(\frac{25}{100}\),3% 表示比率为\(\frac{3}{100}\),100% 表示\(\frac{100}{100}\)或整体。
转换百分比
通过将百分比的值写入分母为 100 的分数并在可能的情况下简化分数,可以将百分比转换为分数。
\[25\%=\dfrac{25}{100}=\dfrac{1}{4}\]
通过将百分比的值写成分母为 100 的分数,然后将分子除以分母,可以将百分比转换为十进制。
\[10\%=\dfrac{10}{100}=0.10\]
要将小数转换为百分比,请将小数写成分数。 如果分数的分母不是 100,则将其转换为分母为 100 的分数,然后将分数写为百分比。
\[0.833=\dfrac{833}{1000}=\dfrac{83.3}{100}=83.3\%\]
要将分数转换为百分比,请先将分数转换为十进制,然后将小数转换为百分比。
\[\dfrac{3}{4}=0.75=\dfrac{75}{100}=75\%\]
假设研究人员发现,每班23名学生中有15名是脑膜炎奈瑟菌携带者。 有多少百分比的学生是携带者? 要找到这个值,首先将数字表示为分数。
\[\mathrm{\dfrac{carriers}{total\: students}}=\dfrac{15}{23}\]
然后将分子除以分母。
\[\dfrac{15}{23}=15\div 23 \approx 0.65\]
最后,要将小数转换为百分比,请乘以 100。
\[0.65 \times 100=65\%\]
携带者的学生比例为65%。
您可能还会获得有关发生和不发生的数据;例如,在学生样本中,有9名学生的弓形虫抗体检测呈阳性,而28名学生的弓形虫抗体检测呈阴性。 血清反应阳性学生的百分比是多少? 第一步是确定 “整体”,积极的学生是其中的一部分。 为此,将阳性和阴性测试相加。
\[\mathrm{positive+negative=9+28=37}\]
整个样本由37名学生组成。 积极因素的比例为:
\[\mathrm{\dfrac{positive}{total\: students}=\dfrac{9}{37}}\]
要求出携带者学生的百分比,请将分子除以分母,然后乘以 100。
\ [\ dfrac {9} {37} =9\ div 37\ 大约 0.24\\
0.24\ times 100=24\%\]
积极学生的比例约为24%。
考虑计算百分比的另一种方法是设置等效分数,其中一个是以 100 为分母的分数,然后进行交叉乘法。 前面的示例将表示为:
\[\dfrac{9}{37}=\dfrac{x}{100}\]
现在,交叉乘法求解未知数:
\ [\ begin {align}
9\ times 100 &=37 x &
\ nonumber\\ [5pt]\ frac {9\ times 100} {37} &=x & &
\ text {将两边除以 37}\ nonnumber\\ [5pt]
24 &\ 大约 x&\ text {Divide}\ nonumber
\ end {align}\]
四舍五入的答案是一样的。
乘以和除以十
在许多领域,尤其是在科学领域,通常将小数乘以 10 的乘方。 让我们看看当我们将 1.9436 乘以 10 的某个幂时会发生什么。
\ [\ begin {align}
1.9436 (10) &=19.436\ nonumber\\
1.9436 (100) &=194.36\ nonumber\\
1.9436 (1000) &=1943.6\ nonumber
\ end {align}\]
小数点移动的位数与十次方中的零数相同。 表\(\PageIndex{1}\)汇总了结果。
| 乘以 | 零 | 小数点移动。。 |
|---|---|---|
| 10 | 1 | 向右 1 个地方 |
| 100 | 2 | 右边 2 个地方 |
| 1,000 | 3 | 右边 3 个地方 |
| 10,000 | 4 | 右边 4 个地方 |
我们可以使用这种模式作为快捷方式来乘以十的乘方,而不是使用垂直格式进行乘法。 我们可以以 10 的幂计算零,然后将小数点向右移动相同数量的位数。
因此,例如,要将 45.86 乘以 100,请将小数点向右移动 2 位。
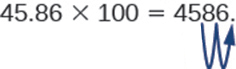
有时候,当我们需要移动小数点时,没有足够的小数位。 在这种情况下,我们使用零作为占位符。 例如,让我们将 2.4 乘以 100。 我们需要将小数点向右移动 2 位。 由于小数点右边只有一位数字,因此我们必须在百分之一处写上 0。
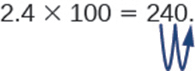
除以 10 的幂时,只需采用相反的方法,将小数向左移动 10 次方中的零数。
让我们看看当我们将 1.9436 除以 10 的某个幂时会发生什么。
\ [\ begin {align}
1.9436\ div 10&=0.19436\ nonumber\\
1.9436\ div 100&=0.019436\ nonumber\\
1.9436\ div 1000&=0.0019436\ non数字
\ end {align}\]
如果没有足够的位数来移动小数,则添加零以创建位置。
科学记数法
科学记数法用于将非常大和非常小的数字表示为两个数字的乘积。 乘积的第一个数字,即数字术语,通常是一个不小于 1 且不大于 10 的数字。 乘积的第二个数字,即指数项,写成带有指数的 10。 表中给出了一些科学记数法的示例\(\PageIndex{2}\)。
| 标准符号 | 科学记数法 |
|---|---|
| 1000 | 1×10 3 |
| 100 | 1×10 2 |
| 10 | 1×10 1 |
| 1 | 1×10 0 |
| 0.1 | 1×10 −1 |
| 0.01 | 1×10 −2 |
对于非常大和非常小的数字,科学记数法特别有用,例如 1,230,000,000 = 1.23×10 9,0.00000000036 = 3.6×10 −10。
用科学记数法表示数字
将任何数字转换为科学记数法很简单。 计算将小数移到最左边的非零数字旁边所需的位数:也就是说,使数字介于 1 到 10 之间。 然后将该数字乘以 10,得出您移动小数点的位数。 如果您将小数向左移动,则指数为正;如果将小数向右移动,则指数为负数。 所以
\[2386=2.386\times1000=2.386\times10^3\]
和
\[0.123=1.23\times0.1=1.23\times10^{-1}\]
10 的幂次(指数)等于小数点移位的位数。
对数
一个数字的常用对数 (log) 是必须将 10 提高到等于该数字的乘方。 例如,100 的常用对数为 2,因为必须将 10 提高到等于 100 的第二个次方。 其他示例见表\(\PageIndex{3}\)。
| 数字 | 指数形式 | 常用对数 |
|---|---|---|
| 1000 | 10 3 | 3 |
| 10 | 10 1 | 1 |
| 1 | 10 0 | 0 |
| 0.1 | 10 −1 | −1 |
| 0.001 | 10 −3 | −3 |
要找到大多数数字的常用对数,你需要使用计算器上的 LOG 按钮。
四舍五入和有效数字
在报告通过测量获得的数值数据时,我们仅使用测量精度所能保证的数量的重要数字。 例如,假设微生物学家使用自动细胞计数器确定一升河水样本中有 525,341 个细菌细胞。 但是,她将浓度记录为每升 525,000 个细胞,并使用这个四舍五入的数字来估计 10 升河水中可能发现的细胞数量。 在这种情况下,测量数量的最后三位数字不算重要。 它们经过四舍五入,以考虑如果测量更多样本时可能出现的细胞数量的变化。
重要数字的重要性在于它们在基础计算中的应用。 除加法和减法外,小数点右边的总和或差值应与计算中使用的数字中最不确定的数字(在以下示例中用下划线表示)中的数字一样多。
假设一位微生物学家想要计算两个琼脂样本的总质量。
\ [\ begin {array} {l}
4.38\ 下划线 {3}\ text {g}\
\ 下划线 {3.002\ 下划线 {1}}\ text {g}\\
7.38\ 下划线 {5}\ text {g}
\ end {array}\]
两个质量中最不确定的有三个小数位,因此总和必须有三位小数。
在乘法和除法中,乘积或商所包含的位数不应超过包含最少有效数字的因子中的位数。 假设微生物学家想计算如果浓度为 0.638 g/mL,则在 6.6 mL 中会有多少试剂存在。
\[\mathrm{0.63\underline{8}\:\dfrac{g}{mL}\times6.\underline{6}\:mL=4.1\:g}\]
同样,答案只有小数点后一位,因为这是计算中最不准确的数字的精度。
四舍五入时,如果保留的数字后面跟着一个大于 5 的数字,则将其增加 1(“向上舍入”)。 如果后面的数字小于 5,请勿更改保留的数字(“向下舍入”)。 如果保留的数字后面跟着 5,则如果保留的数字为奇数,则向上舍入;如果是偶数,则向下四舍五入(四舍五入后,保留的数字将始终为偶数)。
生成时间
如果已知起始像元的数量和倍增时间,则可以随时编写一个方程来计算像元数,只要各单元以恒定速率分裂。 我们将 N 0 定义为细菌的起始数量,时间 t = 0 时的数字。 N i 是时间 t = i(未来任意时间)时的细菌数量。 最后,我们将将 j 设置为等于代数,或者在时间间隔内细胞数量翻倍的次数。 然后我们有,
\[N_i=N_0\times2^j\]
这个方程是二元裂变生长的表达式。
在我们的示例中,N 0 = 4,90 分钟后的代数 j 等于 3,因为生成时间为 30 分钟。 细胞的数量可以通过以下方程估算:
\ [\ begin {align}
n_i&=n_0\ times2^j\ nonumber\\
N_ {90} &=4\ times2^3\ nonumber\\
N_ {90} &=4\ times8=32\ nonnumber
\ end {align}\]
90 分钟后的信元数为 32。