7.A:量子力学(答案)
- Page ID
- 202352
检查你的理解
7.1。 \(\displaystyle (3+4i)(3−4i)=9−16i^2=25\)
7.2。 \(\displaystyle A=\sqrt{2/L}\)
7.3。 \(\displaystyle (1/2−1/π)/2=9%\)
7.4。 \(\displaystyle 4.1×10^{−8}eV; 1.1×10^{−5}nm\)
7.5。 \(\displaystyle 0.5mω^2x^2ψ(x)∗ψ(x)\)
7.6。 无。 第一个函数具有不连续性;第二个函数是双值函数;第三个函数发散,因此不可归一化。
7.7。 a. 9.1%;
b. 25%
7.8。 a. 295 N/m;
b. 0.277 eV
7.9。 \(\displaystyle ⟨x⟩=0\)
7.10。 \(\displaystyle L_{proton}/L_{electron}=\sqrt{m_e/m_p}=2.3%\)
概念性问题
1。 \(\displaystyle 1/\sqrt{L}\),其中\(\displaystyle L=length\);1/L,其中\(\displaystyle L=length\)
3。 波函数不直接对应于任何测量量。 它是预测物理量值的工具。
5。 具有相同波函数的大量粒子的物理量平均值。
7。 是的,如果它的位置完全未知。 是的,如果它的动量完全未知。
9。 不是。 根据不确定性原理,如果粒子位置的不确定性很小,则其动量的不确定性很大。 同样,如果粒子位置的不确定性很大,则其动量的不确定性也很小。
11。 不,这意味着对粒子的预测(用概率表示)与时间无关。
13。 不是,因为粒子在不连续性处以狭窄(无穷小)间隔存在的概率尚未定义。
15。 不是。 对于无限方井,能级之间的间距随着量子数 n 的增加而增加。 测量的最小能量对应于从 n = 2 到 1 的过渡,这是基态能量的三倍。 测量的最大能量对应于从\(\displaystyle n=∞\)到 1 的过渡,即无穷大。 (注意:即使是能量极大的粒子也会绑定在无限方井上,它们永远不能 “逃脱”)
17。 不是。 该能量对应于\(\displaystyle n=0.25\),但 n 必须是整数。
19。 因为简单谐波振荡器的量子数 n 的最小允许值为 0。 不,因为量子力学和经典力学只在大 nn 的极限内一致。
21。 是的,在不确定性原则的限制范围内。 如果振荡粒子是局部化的,则振荡器的动量和能量是分布的。
23。 将屏障宽度加倍
25。 不,无限方孔墙上的粒子上的恢复力是无穷大。
问题
27。 \(\displaystyle ∣ψ(x)∣^2sin^2ωt\)
29。 (a) 和 (e) 可以归一化
31。 a.\(\displaystyle A=\sqrt{2α/π}\);
b.\(\displaystyle probability=29.3%\);
c。\(\displaystyle ⟨x⟩=0⟨x⟩=0\);
d。\(\displaystyle ⟨p⟩=0\);
e。\(\displaystyle ⟨K⟩=α^2ℏ^2/2m\)
33。 a.\(\displaystyle Δp≥2.11×10^{−34}N⋅s\);
b.\(\displaystyle Δv≥6.31×10^{−8}m\);
c。\(\displaystyle Δv/\sqrt{k_BT/m_α}=5.94×10^{−11}\)
35。 \(\displaystyle Δτ≥1.6×10^{−25}s\)
37。 a.\(\displaystyle Δf≥1.59MHz\);
b。\(\displaystyle Δω/ω_0=3.135×10^{−9}\)
39。 进行衍生品收益率\(\displaystyle k^2=\frac{ω^2}{c^2}\)。
41。 对正弦函数执行导数(如上所述)会给出方程右侧的余弦值,因此相等失败。 余弦解也是如此。
43。 \(\displaystyle E=ℏ^2k^2/2m\)
45。 \(\displaystyle ℏ^2k^2ℏ\); 粒子具有一定的动量,因此确定的动量为平方。
47。 9.4 eV,64%
49。 0.38 nm
51。 1.82 MeV
53。 24.7 nm
55。 \(\displaystyle 6.03Å\)
57。 一个。
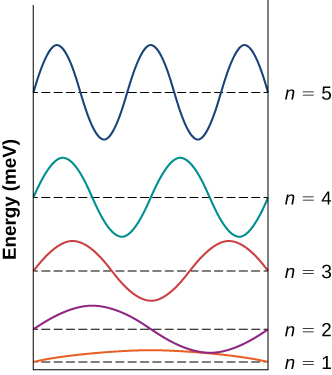
显示了无限方阱中电子的 n=1 到 n=5 态的波函数。 每个函数都由其能量垂直移动,以兆电子伏计量。 n=1 状态是正弦函数的前半波。 n=2 函数是正弦函数的第一个全波。 n=3 函数是正弦函数的前一个半波。 n=4 函数是正弦函数的前两个波浪。 n=5 函数是正弦函数的前两个半波。 ;
b。\(\displaystyle λ_{5→3}=12.9nm,λ_{3→1}=25.8nm,λ_{4→3}=29.4nm\)
59。 证明
61。 \(\displaystyle 6.662×10^{14}Hz\)
63。 \(\displaystyle n≈2.037×10^{30}\)
65。 \(\displaystyle ⟨x⟩=0.5mω^2⟨x^2⟩=ℏω/4\);\(\displaystyle ⟨K⟩=⟨E⟩−⟨U⟩=ℏω/4\)
67。 证明
69。 形式为的复杂函数满足薛定格的时间无关方程。\(\displaystyle Ae^{iϕ}\) 动能和总能的运算符是线性的,因此此类波函数的任何线性组合也是薛定格方程的有效解。 因此,我们得出结论,方程 7.68 满足方程 7.61,方程 7.69 满足方程 7.63。
71。 a. 4.21%;
b. 0.84%;
c. 0.06%
73。 a. 0.13%;
b. 接近 0%
75。 0.38 nm
其他问题
77。 证明
79。 a. 4.0%;
b. 1.4%;
c. 4.0%;
d. 1.4%
81。 a.\(\displaystyle t=mL^2/h=2.15×10^{26}years\);
b。\(\displaystyle E_1=1.46×10^{−66}J,K=0.4J\)
83。 证明
85。 1.2 N/m
87。 0
挑战问题
89。 19.2µm;11.5µm19.2µm;11.5µm
91。 3.92%
93。 证明


