7.7: 粒子穿越潜在屏障的量子隧道
- Page ID
- 202349
在本节结束时,您将能够:
- 描述量子粒子如何穿越潜在屏障
- 确定影响隧道开挖概率的重要物理参数
- 识别观察到量子隧道的物理现象
- 解释量子隧道是如何在现代技术中使用的
量子隧道是一种现象,在这种现象中,粒子穿透势能屏障,其高度大于粒子的总能量。 这种现象既有趣又重要,因为它违反了经典力学原理。 量子隧道在太阳模型中很重要,具有广泛的应用,例如扫描隧道显微镜和隧道二极管。
隧道开挖和潜在能量
为了说明量子隧道,假设一个球沿着表面滚动,动能为 100 J。当球滚动时,它会遇到一座小山。 放置在山顶上的球的势能为 10 J。因此,球(动能 100 J)很容易翻过山坡并继续前进。 在传统力学中,球越过山坡的概率恰好是 1,它每次都会过去。 但是,如果山的高度增加(放置在山顶上的球的潜在能量为 200 J),则球只能在上山的一部分路上移动,停下来,然后朝它来的方向返回。 在球到达山顶之前,球的总能量被完全转换为势能。 即使经过多次尝试,我们也没想到在山外找到 100-J 的球。 因此,球越过山坡的概率恰好为 0,而球被山丘 “反射” 或 “反射” 的概率恰好为 1。 球永远不会越过山坡。 山外球的存在是不可能的,或者 “被大力禁止”。
但是,根据量子力学,球具有波函数,并且该函数是在所有空间上定义的。 波浪函数可能是高度局部化的,但是当球碰到山坡时,总是有可能突然在山上找到球。 事实上,如果球的 “波包” 比屏障宽,这种概率是显而易见的。
观看此交互式模拟,了解隧道开挖的模拟。
用量子力学的语言来说,这座山的特点是潜在的屏障。 有限高度方形屏障由以下势能函数描述:
\ [U (x) =
\ begin {cases}
0,&\ mbox {when} x < 0\\ [4pt] U_0, &\ mbox {when} 0\ leq x\ leq L\\ [4pt] 0, &\ mbox {when} x > L
\ end {cases}\ label {pibPotential}\]
潜在障碍如图所示\(\PageIndex{1}\)。 当屏障的高\(U_0\)度为无限时,代表入射量子粒子的波包无法穿透它,量子粒子会像经典粒子一样从屏障边界反弹。 当屏障\(L\)的宽度为无限且高度有限时,代表入射量子粒子的波包的一部分可以过滤过屏障边界,最终在屏障内移动一段距离后消失。
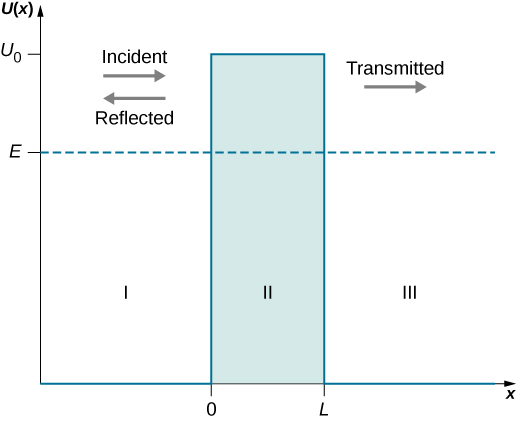
当宽\(L\)度和高度\(U_0\)都有限时,入射在屏障一侧的量子波包的一部分可以穿透屏障边界并继续在屏障内运动,然后在通往另一侧的途中逐渐衰减。 入射量子波包的一部分最终以穿过屏障的传输波包的形式出现在屏障的另一边。 有多少入射波能穿过屏障取决于屏障的宽度\(L\)及其高度\(U_0\),以及入射在屏障上的量子粒\(E\)子的能量。 这就是隧道开挖的物理学。
1927 年,施丁格发表了以他的名字命名的方程后不久,弗里德里希· 汉德首次从理论上分析了量子波函数的屏障穿透力。 一年后,乔治· 加莫利用量子力学的形式主义将原子核的放\(\alpha\)射性衰变解释为一种量子隧道现象。 1957 年隧道二极管的发明清楚地表明,量子隧道对半导体行业很重要。 在现代纳米技术中,单个原子是使用量子隧道知识来操纵的。
隧道和波函数
假设能量沿 x 轴(向右正方向)\(E\)传播的均匀且不受时间限制的电子束或其他量子粒子遇到了方程\ ref {pibPotental} 描述的势垒。 问题是:光束中的单个粒子穿过潜在屏障的概率是多少? 答案可以通过求解光束中粒子与时间无关的 Schrdinger 方程的边界值问题来找到。 该方程的一般形式由方程\ ref {TISE} 给出,我们在此重现该方程:
\[-\frac{\hbar^2}{2m} \frac{d^2\psi(x)}{dx^2} + U(x)\psi(x) = E\psi(x), \label{TISE} \]
哪里\(-\infty < x < +\infty\)。
方程\ ref {TISE}\(U(x)\) 中的势函数由方程\ ref {pibPotental} 定义。 我们假设传入粒子的给定能量\(E\)小于潜在屏障的高度\(U_0\)\(E < U_0\),因为这是有趣的物理案例。 知道传入粒\(E\)子的能量后,我们的任务是求解方程\ ref {TISE}\(\psi(x)\),求解一个连续且所有 x 都具有连续一阶导数的函数。 换句话说,我们正在寻找一个 “外观平滑” 的解(因为波函数就是这样),它可以给出概率解释,\(|\psi(x)|^2 = \psi^*(x)\psi(x)\)这就是概率密度。
我们将实轴分成三个区域,其边界由方程\ ref {pibPotental} 中的势函数定义(如图所示\(\PageIndex{1}\)),每个区域的转录方程\ ref {TISE}。 用区域\(\psi_I(x)\)内的解\(x < 0\)、区域\(I\)\(\psi_{II}(x)\)内的解和区域\(II\)内的解表示\(0 \leq x \leq L\),平稳薛定格方程在这三个区域中具有以下形式:\(\psi_{III}(x)\)\(III\)\(x > L\)
\[-\dfrac{\hbar^2}{2m} \frac{d^2\psi_I(x)}{dx^2} = E\psi_I(x), \label{R1} \]
在区域\(I\):\(-\infty < x < 0,\)
\[-\dfrac{\hbar^2}{2m} \frac{d^2\psi_{II}(x)}{dx^2} + U_0\psi_{II}(x) = E\psi_{II}(x) \label{R2} \]
在区域\(II\):\(0 < x < L,\)
\[-\dfrac{\hbar^2}{2m} \frac{d^2\psi_{III}(x)}{dx^2} = E\psi_{III}(x) \label{R3} \]
在区域\(III\):\(L < x < +\infty,\)
区域边界的连续性条件要求:
\[\psi_I(0) = \psi_{II}(0) \label{Bound1} \]
在区域之间的边界\(I\)和\(II\)
和
\[\psi_{II}(L) = \psi_{III}(L) \label{Bound2} \]
在区域和\(II\)之间的边界\(III\)。
“平滑度” 条件要求解的一阶导数在区域边界处是连续的:
\[ \left.\dfrac{d\psi_I(x)}{dx}\right|_{x = 0} = \left.\dfrac{d\psi_{II}(x)}{dx}\right|_{x = 0} \label{smooth1} \]
在区域之间的边界\(I\)和\(II\)
和
\[ \left.\dfrac{d\psi_{II}(x)}{dx}\right|_{x = L} = \left.\dfrac{d\psi_{III}(x)}{dx}\right|_{x = L} \label{smooth2} \]
在区域和\(II\)之间的边界\(III\)。
在接下来的内容中,我们找到了函数\(\psi_I(x), \, \psi_{II}(x)\)和\(\psi_{III}(x)\)。
我们可以很容易地验证(通过代入原始方程并进行微分)\(III\),在区域和\(I\)中,解必须采用以下一般形式:
\[\psi_I(x) = Ae^{+ikx} + Be^{-ikx} \label{Eq5A} \]
\[\psi_{III}(x) = Fe^{+ikx} + Ge^{-ikx} \label{Eq5B} \]
其中\(k = \sqrt{2mE}/\hbar\)是波数,复数指数表示振荡,
\[e^{\pm ikx} = \cos \, kx \pm i \, \sin \, kx. \nonumber \]
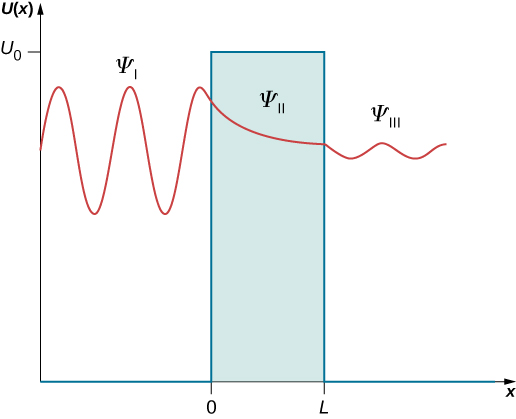
方程\ ref {Eq5A} 和\ ref {Eq5B}\(G\) 中的常量\(A\)\(F\)、、和可能很复杂。\(B\) 这些解决方案如图所示\(\PageIndex{2}\)。 在区域 I 中,有两个波浪——一个是入射的(向右移动),另一个是反射的(向左移动)——因此方程\ ref {Eq5A}\(B\) 中的常数\(A\)都不会消失。 在区域 III 中,只有一个波浪(向右移动),即发射波,因此方程\ ref {Eq5B} 中的常数\(G\)必须为零\(G = 0\)。 我们可以明确地写出入射波是\(\psi_{in}(x) = Ae^{+ikx}\),反射波是\(\psi_{ref}(x) = Be^{-ikx}\),发射波是\(\psi_{tra}(x) = Fe^{+ikx}\)。 入射波的振幅为
\[ \begin{align*}|\psi_{in}(x)|^2 &= \psi_{in}^*(x)\psi_{in}(x) \\[4pt] &= (Ae^{+ikx})^*Ae^{+ikx} \\[4pt] &= A^*e^{-ikx}Ae^{+ikx} \\[4pt] &= A^*A = |A|^2. \end{align*} \nonumber \]
同样,反射波的振幅为\(|\psi_{ref}(x)|^2 = |B|^2\),发射波的振幅为\(|\psi_{tra}(x)|^2 = |F|^2\)。 我们从波浪理论中知道,波浪振幅的平方与波浪强度成正比。 如果我们想知道有多少入射波穿过屏障,我们需要计算发射波振幅的平方。 传输概率或隧道开挖概率是传输强度 (\(|F|^2\)) 与入射强度 (\(|A|^2\)) 之比,写为
\[ \begin{align} T(L, E) &= \frac{|\psi_{tra}(x)|^2}{|\psi_{in}(x)|^2} \\[4pt] &= \frac{|F|^2}{|A|^2} \\[4pt] &= \left|\frac{F}{A}\right|^2 \label{trans} \end{align} \]
其中\(L\)是屏障的宽度,\(E\)是粒子的总能量。 这是入射光束中的单个粒子穿过潜在屏障的概率。 直观地说,我们知道这个概率必须取决于屏障的高度\(U_0\)。
在区域 II 中,方程式\ ref {R2} 中的项可以重新排列为
\[\frac{d^2\psi_{II}(x)}{dx^2} = \beta^2 \psi_{II}(x) \label{eq10} \]
其中\(\beta^2\)是正数\(U_0 > E\),因为参数\(\beta\)是实数,
\[\beta^2 = \frac{2m}{\hbar^2}(U_0 - E). \label{eq20} \]
方程\ ref {eq10} 的一般解不是振荡的(与其他区域不同)\(\psi_{II}(x)\),而是以指数的形式表示逐渐衰减
\[\psi_{II}(x) = Ce^{-\beta x} + De^{+\beta x}. \label{eq25B} \]
图中说明了这三个区域中的两种类型的解决方案\(\PageIndex{2}\)。
现在我们使用边界条件来查找未知常量的方程。 方程\ ref {Eq5A} 和\ ref {eq25b} 被替换成方程\ ref {Bound1} 来给出
\[A + B = C + D. \nonumber \]
方程\ ref {eq25b} 和\ ref {Eq5B} 被替换成方程\ ref {Bound2} 来给出
\[Ce^{-\beta L} + De^{+\beta L} = Fe^{+ik L}. \nonumber \]
同样,我们将方程\ ref {Eq5A} 和\ ref {eq25b} 替换为方程\ ref {smooth1},然后进行微分并获得
\[-ik(A - B) = \beta(D - C). \nonumber \]
同样,边界条件方程\ ref {smooth2} 显式读取
\[\beta (De^{+\beta L} - Ce^{-\beta L}) = +ikFe^{+ikL}. \nonumber \]
我们现在有四个方程来表示五个未知常量。 但是,由于我们所追求的量是传输系数 (\(T\)),在方程\ ref {trans} 中由分数定义\(F/A\),因此方程的数量完全正确,因为当我们将上述每个方程除以时\(A\),最终只有四个未知分数:\(B/A\)、\(C/A\)\(D/A\)、和\(F/A\),其中三个可以省去找到\(F/A\)。 导致表达式的实际代数\(F/A\)相当长,但可以手工完成,也可以借助计算机软件完成。 最终结果是
\[\frac{F}{A} = \frac{e^{-ikL}}{\cosh \, (\beta L) + i (\gamma /2) \, \sinh \, (\beta L)}. \label{eq40} \]
在推导方程\ ref {eq40} 时,为了避免混乱\(\gamma \equiv \beta/k - k/\beta\),我们使用替换和双曲函数的定义:
\[\cosh \, y = \frac{e^y + e^{-y}}{2} \nonumber \]
和
\[\sinh \, y = \frac{e^y - e^{-y}}{2}. \nonumber \]
我们将方程\ ref {eq40} 替换为方程\ ref {trans},然后获得屏障传输系数的精确表达式,
\[T(L,E) = \left(\frac{F}{A}\right)^*\frac{F}{A} = \frac{e^{+ikL}}{\cosh \, (\beta L) - i (\gamma /2) \, \sinh \, (\beta L)} \cdot \frac{e^{-ikL}}{\cosh \, (\beta L) + i (\gamma /2) \, \sinh \, (\beta L)}. \nonumber \]
要么
\[T(L,E) = \frac{1}{\cosh^2 \, (\beta L) + (\gamma /2)^2 \, \sinh^2 \, (\beta L)}. \label{eqTrans1} \]
哪里
\[\left(\frac{\gamma}{2}\right)^2 = \frac{1}{4}\left( \frac{1 - E/U_0}{E/U_0} + \frac{E/U_0}{1 - E/U_0} - 2\right). \nonumber \]
对于传输不佳的宽而高的屏障,方程\ ref {eqTrans1} 可以近似为
\[T(L,E) \approx 16 \frac{E}{U_0}\left(1 - \dfrac{E}{U_0}\right) e^{-2\beta L}. \label{eqTrans2} \]
无论是精确表达式(方程\ ref {eqTrans1})还是近似表达式(方程\ ref {eqTrans2}),我们都会发现隧道效应在很大程度上取决于潜在屏障\(L\)的宽度。 在实验室中,我们可以调整潜在的高\(U_0\)度和宽度,\(L\)以设计具有理想传输系数的纳米器件。
两根铜纳米线由氧化铜纳米层绝缘,该层提供 10.0 eV 的电位屏障。 估计 7.00-eV 电子穿过 5.00-nm 厚氧化层的纳米线之间的隧穿概率。 如果该层的厚度减少到只有 1.00 nm 会怎样? 如果电子的能量增加到 9.00 eV 会怎样?
策略
我们使用方程式\ ref {eqTrans2} 将绝缘氧化物层视为有限高度的电位屏障。 我们确定\(U_0 = 10.0 \, eV, \, E_1 = 7.00 \, eV, \, E_2 = 9.00 \, eV, \, L_1 = 5.00 \, nm\), 和\(L_2 = 1.00 \, nm\). 我们使用方程\ ref {eq20} 来计算指数。 另外,我们需要电子的剩余质量\(m = 511 \, keV/c^2\)和普朗克常数\(\hbar = 0.1973 \, keV \cdot nm/c\)。 这种类型的估算通常用于处理通常不适合手持式计算器的非常小的量。 为了正确估算订单,我们会进行转换\(e^y = 10^{y/ln \, 10}\)。
解决方案
常量:
\[\frac{2m}{\hbar^2} = \frac{2(511 \, keV/c^2)}{(0.1973 \, keV \cdot nm/c^2)^2} = 26,254 \frac{1}{keV \cdot (nm)^2}, \nonumber \]
\[\beta = \sqrt{\frac{2m}{\hbar^2}(U_0 - E)} = \sqrt{26,254\frac{(10.0 \, eV - E)}{keV \cdot (nm)^2}} = \sqrt{26.254(10.00 - E)/eV} \frac{1}{nm}.\nonumber \]
对于具有以下特性的低能电子\(E_1 = 7.00 \, eV\):
\[\beta_1 = \sqrt{26.254(10.00 \, eV - E_1)/eV}\frac{1}{nm} = \sqrt{26.254(10.00 - 7.00)}\frac{1}{nm} = \frac{8.875}{nm},\nonumber \]
\[T(L,E) = 16\frac{E_1}{U_0}\left(1 - \frac{E_1}{U_0}\right)e^{-2\beta_1L} = 16\frac{7}{10}\left(1 - \frac{7}{10}\right)e^{-17.75 \, L/nm} = 3.36 \, e^{-17.75 \, L/nm}\nonumber \]
对于具有以下特性的更高能量电子\(E_2 = 9.00 \, eV\):
\[\beta_2 = \sqrt{26.254(10.00 \, eV - E_2)/eV}\frac{1}{nm} = \sqrt{26.254 (10.00 - 9.00)}\frac{1}{nm} = \frac{5.124}{nm},\nonumber \]
\[T(L,E_2) = 16\frac{E_2}{U_0}\left( 1 - \frac{E_2}{U_0}\right) e^{-2\beta_2 L} = 16 \frac{9}{10} \left(1 - \frac{9}{10}\right) e^{-10.25 \, L/nm} = 1.44 \, e^{-10.25 \, L/nm}\nonumber \]
使用以下方法获得广泛的屏障\(L_1 = 5.00 \, nm\):
\[T(L_1,E_1) = 3.36 e^{-17.75 \, L_1/nm} = 3.36 e^{-17.75 \cdot 5.00 nm/nm} = 3.36e^{-88} = 3.36(6.2 \times 10^{-39}) = 2.1\% \times 10^{-36}\nonumber \]
\[T(L_1,E_2) = 1.44 e^{-10.25 \, L_1/nm} = 1.44 e^{-10.25 \cdot 5.00 \, nm/nm} = 1.44^{-51.2} = 1.44(5.81 \times 10^{-12}) = 8.36\% \times 10^{-25}\nonumber \]
对于较窄的屏障,请使用\(L_2 = 1.00 \, nm\):
\[T(L_2,E_1) = 3.36e^{−17.75 \, L_2/nm} = 3.36 e^{−17.75 \cdot 1.00 \, nm/nm} = 3.36 e^{−17.75} = 3.36(5.1 \times 10^{−7}) = 1.7\% \times 10^{−4},\nonumber \]
\[T(L_2,E_2) = 1.44e^{−10.25 \, L_2/nm} = 1.44e^{-10.25 \cdot 1.00 \, nm/nm} = 1.44e^{−10.25} = 1.44(3.53 \times 10^{−5}) = 5.09\% \times 10^{-7}.\nonumber \]
意义
从这些估计中我们可以看出,隧道开挖的概率更多地受潜在屏障宽度的影响,而不是入射粒子的能量的影响。 在当今的技术中,我们可以操纵金属表面上的单个原子,以形成几分之一纳米的潜在屏障,从而产生可测量的隧道电流。 该技术的众多应用之一是扫描隧道显微镜 (STM),我们将在本节后面讨论该显微镜。
动能 1.00 eV 的质子入射在高度为 10.00 eV 的方形势垒上。 如果质子要与具有相同能量的电子具有相同的传输概率,那么屏障的宽度相对于电子遇到的屏障宽度必须是多少?
- 回答
-
\[L_{proton}/L_{electron} = \sqrt{m_e/m_p} = 2.3\% \nonumber \]
放射性衰变
1928年,Gamow将量子隧道确定为导致原子核放射性衰变的机制。 他观察到,钍、铀和铋的某些同位素通过发射 α-粒子(双电离氦原子,或者简而言之,氦核)而分解。 在发射 α-particle 的过程中,原始原子核被转化为新的原子核,其中子比原始原子核少两个中子和两个质子。 一种同位素发射的α粒子具有大致相同的动能。 当我们观察各种元素的同位素之间这些能量的变化时,最低动能约为4兆电子伏,最高动能约为9兆电子伏,因此这些能量具有相同的数量级。 这是关于各种同位素之间相似之处的终点。
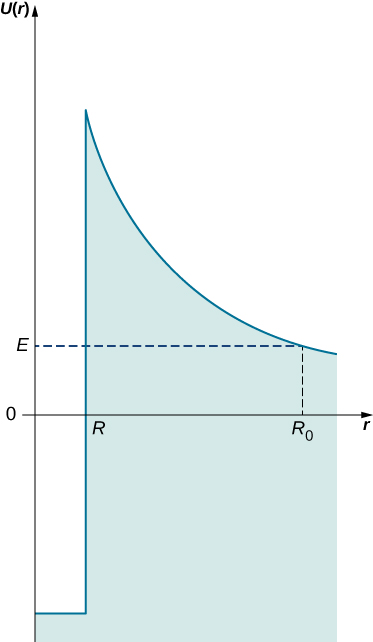
当我们检查半衰期(半衰期是放射性样品因衰变而失去一半原子核的时间)时,不同的同位素差异很大。 例如,polonium-214的半衰期为160微秒,铀的半衰期为45亿年。 Gamow 通过考虑原子核的 “球盒” 模型来解释这种变化,其中 α-particle 可以作为自由粒子在墙之间来回反弹。 封闭是由盒子球形墙上的强大核电位提供的。 但是,这堵墙的厚度不是无限的,而是有限的,因此原则上,核粒子有机会逃脱这种核封锁。 封闭屏障的内墙上有很高的核电位,它使 α-particle 处于很小的封闭状态。 但是,当一个 α-particle 进入这堵墙的另一边时,它会受到静电库仑排斥并远离原子核。 这个想法如图所示\(\PageIndex{3}\)。 将α粒子与外界分开的势垒的宽\(L\)度取决于粒子的动能\(E\)。 此宽度是以核半径标记的点\(R\)与屏障另一侧出现 α-particle 的点\(R_0\)之间的距离\(L = R_0 - R\)。 在远处\(R_0\),它的动能必须至少与排斥的静电能相匹配\(E = (4\pi\epsilon_0)^{-1}Ze^2/R_0\)(其中 +Ze 是原子核的电荷)。 这样我们就可以估计核屏障的宽度,
\[L = \frac{e^2}{4\pi\epsilon_0} \frac{Z}{E} - R. \nonumber \]
从这个估计中我们可以看出,α-particle 的能量越高,它要穿过的屏障的宽度就越窄。 我们还知道,潜在屏障的宽度是隧道开挖概率中最重要的参数。 因此,高能的α粒子有很大的机会逃离原子核,而且,对于这样的原子核,核分解的半衰期很短。 请注意,这个过程是高度非线性的,这意味着α粒子能量的微小增加会对隧道开挖概率产生不成比例的巨大增强作用,从而缩短半衰期。 这就解释了为什么发射 8 兆电子伏α粒子的钯的半衰期只有数百毫秒,而发射 4-meV α-粒子的铀的半衰期为数十亿年。
场发射
场发射是一种从导电表面发射电子的过程,这是由于在垂直于表面的方向上施加了强大的外部电场(图\(\PageIndex{4}\))。 正如我们在前面章节中对电场的研究中所知道的那样,施加的外部电场会使导体中的电子移动到其表面并停留在那里,只要目前的外场不太强。 在这种情况下,我们在整个导体内部(包括其表面)都有恒定的电势。 用势能的语言来说,我们说导体内部的电子具有恒定的势能\(U(x) - -U_0\)(在这里,x 表示导体内部)。
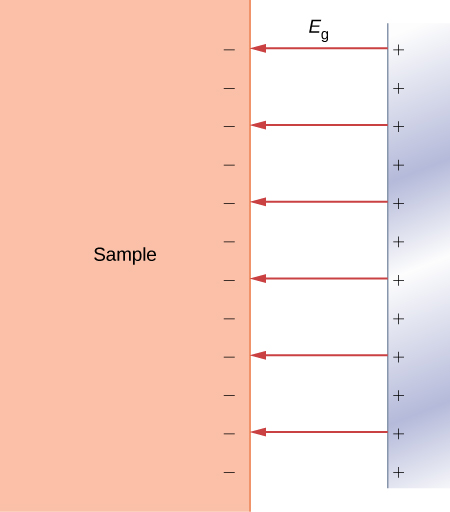
在图中所示的情况下\(\PageIndex{4}\),外部电场均匀且具有大小\(E_g\),如果电子碰巧位于导体外部,距离其表面 x 的距离,则其势能必须为\(U(x) = -eE_gx\)(此处,x 表示到表面的距离)。 取表面的起点,\(x = 0\)即表面的位置,我们可以将金属中传导电子的势能表示为图中所示的潜在能量屏障\(\PageIndex{5}\)。 在没有外部场的情况下,势能变成由\(U(x \leq 0) = -U_0\)和定义的阶梯屏障\(U(x > 0) = 0\)。
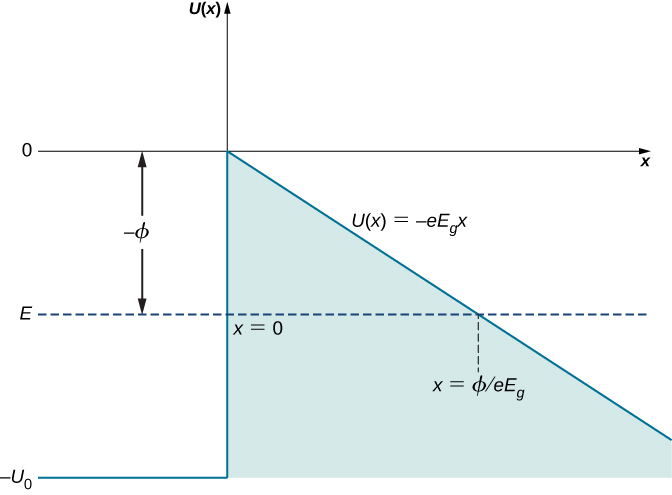
当外部电场强时,表面的传导电子可能会脱离外场,并沿着电场线向与外场反平行的方向加速,远离表面。 简而言之,传导电子可能会从表面逸出。 场发射可以理解为传导电子穿过导体表面的势垒的量子隧道。 这里起作用的物理原理与放射性原子核的α发射机制非常相似。
假设传导电子具有动能 E(金属中电子的平均动能是金属的功函数,可以测量,如光子和物质波中的光电效应所述),外部电场可以是局部的由均匀的强度电场近似\(E_g\)。 电子必须穿过的势垒的宽度 L 是从导体表面到表面外点的距离,在该点的动能与其在外场中的势能值相匹配。 在图中\(\PageIndex{5}\),这个距离是沿着\(U(x) = E\)从\(x = 0\)到截距的水平虚线测量的\(U(x) = -eE_gx\),因此屏障宽度为
\[L = \frac{e^{-1}E}{E_g} = \frac{e^{-1}\phi}{E_g} \nonumber \]
我们看到 L 与外场\(E_g\)的强度成反比。 当我们增加外场的强度时,对于具有给定动能的电子,导体外部的势垒会变得更陡峭,其宽度也会减小。 反过来,电子穿过屏障(导体表面)的概率成倍增加。 出现在屏障另一侧的电子形成了可以在表面上方探测到的电流(隧道电子电流)。 隧道电子电流与隧穿概率成正比。 隧道开挖概率以非线性方式取决于屏障宽度 L,L 可以通过调整来改变\(E_g\)。 因此,可以通过调整表面外部电场的强度来调整隧道电子电流。 当外部电场的强度恒定时,隧道电子电流在地表以上的不同高度 L 处具有不同的值。
我们刚才描述的金属表面的量子隧道现象是Gerd Binnig和Heinrich Rohrer于1981年发明的扫描隧道显微镜(STM)运行背后的物理原理。 STM 设备由扫描尖端(通常由钨、铂铱或金制成的针头);压电设备,用于在待扫描表面上方 0.4 至 0.7 nm 的典型范围内控制尖端高度;控制尖端沿表面运动的设备;以及计算机显示图像。 当样品保持适当的电压偏置时,扫描尖端沿表面移动(图\(\PageIndex{6}\)),尖端和表面之间的隧道电子电流记录在每个位置。
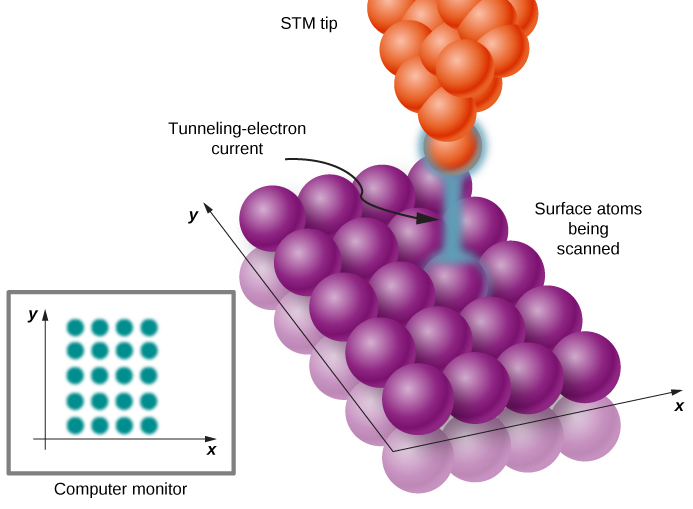
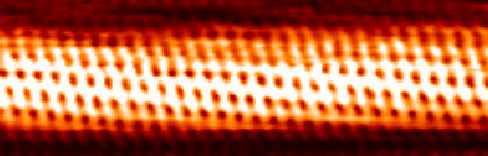
电流量取决于电子从表面隧穿到尖端的概率,而这反过来又取决于尖端在表面之上的仰角。 因此,在每个尖端位置,从尖端到表面的距离是通过测量有多少电子从表面隧道到尖端来测量的。 这种方法可以提供前所未有的分辨率,约为0.001 nm,约为原子平均直径的1%。 通过这种方式,我们可以看到表面上的单个原子,如图中碳纳米管的图像\(\PageIndex{7}\)。
共振量子隧道
量子隧道在半导体器件中有许多应用,例如以纳米尺度设计的电子电路元件或集成电路;因此被称为 “纳米技术”。 例如,二极管(一种电路元件,当偏置电压的极性反向时,它会导致一个方向的电子电流与相反方向的电流不同)可以通过两种不同类型的半导体材料之间的隧道结来实现。 在这样的隧道二极管中,电子在两个不同半导体之间的接触处穿过单个电位势垒。 在交界处,隧道电子电流随结上施加的电位差呈非线性变化,并可能随着偏置电压的增加而迅速降低。 这与我们在家用电路中熟悉的欧姆定律行为不同。 这种快速行为(由量子隧道引起)在高速电子设备中是理想的。
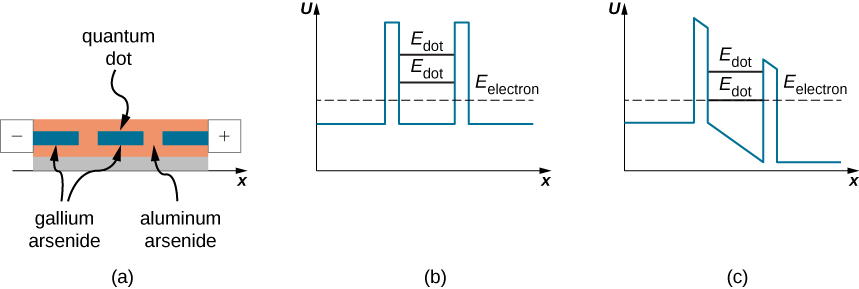
另一种电子纳米器件利用电子的共振隧道穿过量子点中存在的潜在屏障。 量子点是半导体纳米晶体的一个小区域,例如在硅或砷化铝晶体中生长。 图中\(\PageIndex{8a}\)显示了嵌入砷化铝晶圆中的砷化镓量子点。 量子点区域充当有限高度的潜在井(图\(\PageIndex{8b}\)),在点边界上有两个有限高度的潜在屏障。 同样,对于盒子(即无限势井)中的量子粒子,捕获在有限高度势阱中的量子粒子的低位能量是量化的。 盒子和井势之间的区别在于,盒子中的量子粒子具有无限数量的量化能量,并且会被无限期地困在盒子中,而捕获在势井中的量子粒子具有有限数量的量化能级,可以穿越电位井界处的障碍物通往井外。 因此,位于砷化铝中的砷化镓量子点是量化电子低位能量的潜在井,如\(E_{dot}\)图(b)部分所示。 当电子在点外部区域的能\(E_{electron}\)量与其在点中的\(E_{dot}\)能量不匹配时,电子不会穿过点的区域,也没有电流通过这样的电路元件,即使它保持在电压差下(偏见)。 但是,当这种电压偏置的变化使其中一个屏障降低,从而使\(E_{dot}\)之对齐\(E_{electron}\)时,如图(c)部分所示,电子电流会流过该点。 现在,当电压偏置增加时,这种校准会丢失,电流停止流动。 当电压偏差进一步增加时,在偏置电压达到外部电子能量与点中下一个电子能量水平相匹配的值之前,电子隧道变得不可能。 设备名称中的 “共振” 一词表示只有在通过调整施加的电压偏置来匹配选定的能量水平时,才会出现隧道电子电流,例如在刚才描述的谐振隧穿二极管的工作机制中。 谐振隧道二极管用作超快的纳米开关。