7.6: 量子谐波振荡器
- Page ID
- 202307
在本节结束时,您将能够:
- 描述量子谐波振荡器的模型
- 识别谐波振荡器的经典模型和量子模型之间的差异
- 解释经典模型和量子模型重合的物理情况
振荡存在于整个自然界中,例如电磁波、振动分子和树枝轻柔的来回摇摆。 在前面的章节中,我们使用牛顿力学来研究宏观振荡,例如弹簧上的方块和简单的摆锤。 在本章中,我们将开始使用量子力学研究振荡系统。 我们首先回顾一下经典的谐波振荡器。
经典谐波振荡器
简单的谐波振荡器是指围绕平衡位置进行谐波运动的粒子或系统,例如弹簧上有质量振动的物体。 在本节中,我们只考虑一维振荡。 假设质量围绕平衡位置沿着\(x\)-方向来回移动\(x = 0\)。 在经典力学中,粒子根据给出的线性恢复力而移动\(F_x = -kx\),其中\(x\)是粒子从其平衡位置移动。 运动发生在两个转折点之间\(x \pm A\),其中 A 表示运动的振幅。 物体的位置随着时间的推移周期性变化\(\omega = \sqrt{k/m}\),角频率取决于振荡器的质量 m 和净力的力常数\(k\),可以写成
\[x(t) = A \, \cos (\omega t + \phi). \label{7.52} \]
振荡\(E\)器的总能量是其动能\(K = mu^2/2\)和力的弹性势能之和\(U(x) = kx^2/2\),
\[E = \dfrac{1}{2} mu^2 + \dfrac{1}{2}kx^2. \label{7.53} \]
在转折点\(x = \pm A\),振荡器的速度为零;因此,在这些点,振荡能量仅以势能的形式出现\(E = kA^2/2\)。 振荡器的势能与其位置\(U(x)\)的关系图\(x\)是抛物线(图\(\PageIndex{1}\))。 势能函数是相对于平衡位置测量的\(x\)二次函数。 在同一张图上,我们还将振荡器的总能量\(E\)绘制成一条水平线,该水平线截住抛物线\(x = \pm A\)。 然后,动能表示\(K\)为总能量线和势能抛物线之间的垂直距离。
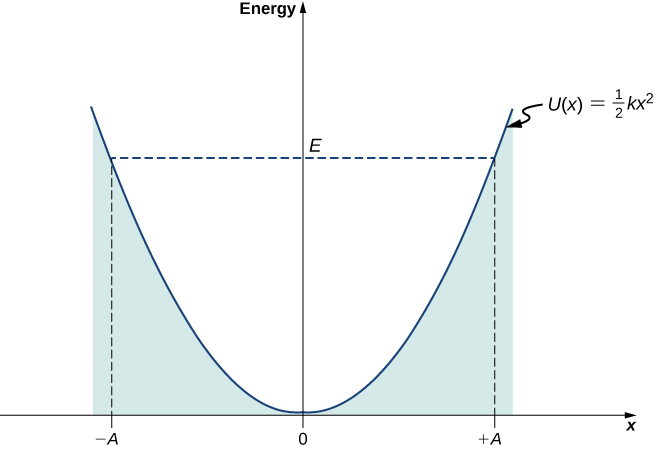
在此图中,经典振荡器的运动仅限于其动能为非负的区域,这就是能量关系方程\ ref {7.53} 所说的。 从物理上讲,这意味着除了转折点之外永远找不到传统振荡器,它的能量仅取决于转折点与其平衡位置的距离。 传统振荡器的能量以连续的方式变化。 传统振荡器可能具有的最低能量为零,这与物体在其平衡位置处于静止状态的情况相对应。 传统振荡器的零能量状态仅意味着没有振荡,根本没有运动(图中一个位于电位井底部的经典粒子\(\PageIndex{1}\))。 当物体振荡时,无论其能量有多大或多小,它在转折点附近停留的时间最长,因为这是它减速并反转运动方向的地方。 因此,在转折点附近找到经典振荡器的概率最高,而在平衡位置找到经典振荡器的概率最低。 (请注意,这并不是表示物体倾向于降低能量。 它是关于物体在各个区域中移动的速度的陈述。)
量子谐波振荡器
这种经典表述的一个问题是它并不普遍。 例如,我们不能用它来描述双原子分子的振动,在这种振动中,量子效应很重要。 量子公式的第一步是使用经典表达式\(k = m\omega^2\)来限制对原子之间的 “弹簧” 常数的提及。 通过这种方式,势能函数可以用更通用的形式书写,
\[U(x) = \dfrac{1}{2}m \omega^2 x^2. \label{7.54} \]
将这个表达式与与时间无关的薛定格方程相结合,可以得出
\[-\dfrac{\hbar}{2m} \dfrac{d^2 \psi(x)}{dx^2} + \dfrac{1}{2}m\omega^2 x^2 \psi(x) = E\psi (x). \label{7.55} \]
为了求解方程\ ref {7.55},也就是说,要找到允许的能量\(E\)及其相应的波函数,我们要求波函数围绕\(x = 0\)(势井的底部)对称并且可以归一化。\(\psi (x) \) 这些条件确保在从\(-\infty\)到的整个 x 范围内进行积分时,概率密度\(|\psi (x)|^2\)必须是有限的\(+\infty\)。 如何求解方程\ ref {7.55} 是量子力学更高级课程的主题;在这里,我们仅引用结果。 允许的能量是
\[ \begin{align} E_n &= \left(n + \dfrac{1}{2}\right) \hbar \omega \\[5pt] &= \dfrac{2n + 1}{2} \hbar \omega \label{7.56} \end{align} \]
和\(n = 0,1,2,3,...\)
与这些能量(固定状态或定能量状态)相对应的波函数是
\[\psi_n (x) = N_n e^{-\beta^2 x^2/2} H_n (\beta x), \, n = 0,1,2,3, ... \label{7.57} \]
其中\(\beta = \sqrt{m\omega/\hbar}\),\(N_n\)是归一化常数,\(H_n(y)\)是一个度数多项式,\(n\)称为 Hermite 多项式。 前四个 Hermite 多项式是
- \(H_0 (y) = 1\)
- \(H_1 (y) = 2y\)
- \(H_2 (y) = 4y^2 - 2\)
- \(H_3 (y) = 8y^3 - 12 y.\)
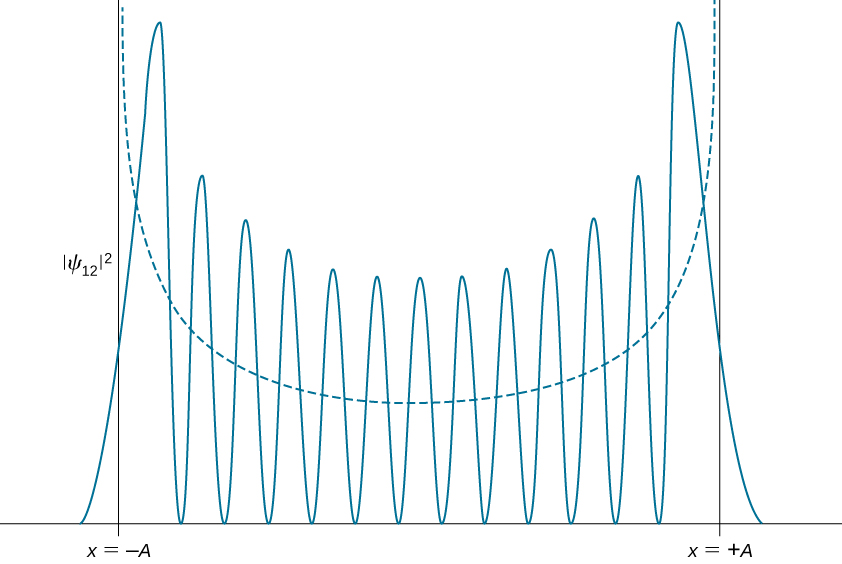
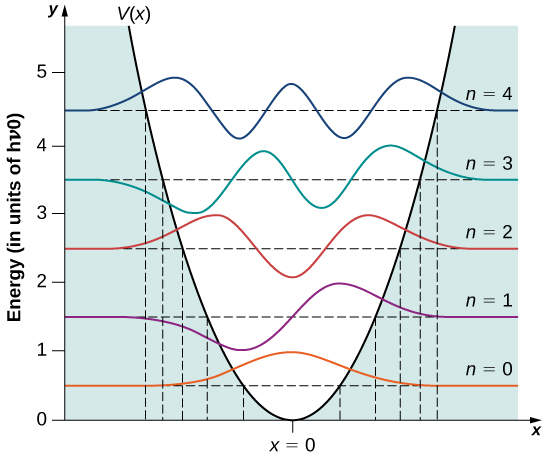
图中给出了一些示例波函数\(\PageIndex{2}\)。 随着主数值的增加,解在偶数函数和奇数函数之间交替出现\(x = 0\)。
找出能\(A\)量等于量子态中量子振荡器的能量的经典振荡器的振荡幅度\(n\)。
策略
为了确定振幅\(A\),我们将经典能量设置为\(E = kx^2/2 = m\omega^2 \, A^2/2\)等于方程\ ref {7.56}\(E_n\) 给出的能量。
解决方案
我们获得
\[\begin{align} E_n &= m\omega^2 A_n^2/2 \nonumber \\[5pt] A_n &= \sqrt{\dfrac{2}{m\omega^2}E_n} \nonumber \\[5pt] &= \sqrt{\dfrac{2}{m\omega^2} \dfrac{2n + 1}{2}\hbar \omega} \nonumber \\[5pt] &= \sqrt{(2n + 1) \dfrac{\hbar}{m\omega}}. \nonumber \end{align} \nonumber \]
意义
随着量子数 n 的增加,振荡器的能量以及振荡幅度的增加(对于固定的自然角频率)。 对于大 n,振幅与量子数的平方根大致成正比。
此解决方案中出现了几个有趣的功能。 与传统振荡器不同,量子振荡器的测量能量只能具有方程\ ref {7.56} 给出的能量值。 此外,与盒子中的量子粒子不同,允许的能级间隔均匀,
\[\begin{align} \Delta E &= E_{n+1} - E_n \\[5pt] &= \dfrac{2(n + 1) + 1}{2} \hbar \omega - \dfrac{2n + 1}{2} \hbar \omega \\[5pt] &= \hbar \omega = hf. \label{7.58} \end{align} \]
当绑定到这样一个系统的粒子从高能状态过渡到低能量状态时,发射的光子携带的最小能量子必然是\(hf\)。 同样,当粒子从低能态过渡到高能态时,粒子可以吸收的最小能量子是\(hf\)。 量子振荡器只能以这种能量最小的量子的倍数吸收或发射能量。 这与普朗克关于黑体辐射问题中辐射和空腔壁之间能量交换的假设是一致的。
\(\ce{HCl}\)双原子分子由一个氯原子和一个氢原子组成。 由于氯原子的质量是氢原子的35倍,因此假设氯原子静止不动,H原子由于胡克定律建模的弹性分子力而产生谐波振荡,就可以很好地近似得出分子的振动。\(\ce{HCl}\) 为氯化氢测得的红外振动光谱的最低频率线以中心为中心\(f = 8.88 \times 10^{13} Hz\)。 这个分子的振动能量之间的间距是多少? HCl 分子中原子键的力常数 k 是多少?
策略
最低频率线对应于最低频率光子的发射。 当分子在两个相邻的振动能级之间过渡时,就会发射这些光子。 假设能级间距相等,我们使用方程\ ref {7.58} 来估计间距。 通过将氯原子视为无限重,将H原子视为进行振荡的质量,\(m\)可以很好地近似化该分子。 将这个分子系统视为经典的振荡器,力常数是从经典关系中找到的\(k = m\omega^2\)。
解决方案
能量间距为
\[ \begin{align} \Delta E &= hf \nonumber \\[5pt] &= (4.14 \times 10^{-15} eV \cdot s)(8.88 \times 10^{13} Hz) \nonumber\\[5pt] &= 0.368 \, eV. \nonumber \end{align} \nonumber \]
力常数为
\[ \begin{align} k &= m \omega^2 \nonumber \\[5pt] &= m (2\pi f)^2 \nonumber \\[5pt] &= (1.67 \times 10^{ −27} kg)(2\pi \times 8.88 \times 10 ^{13}Hz)^2 \nonumber \\[5pt] &= 520 \, N/m. \nonumber \end{align} \nonumber \]
意义
HCl 分子中原子之间的力异常强大。 振动等级之间的能量转换中释放的典型能量在红外范围内。 正如我们稍后将看到的那样,双原子分子振动能级之间的过渡通常伴随着旋转能级之间的过渡。
碘化氢 HI 双原子分子的振动频率为\(6.69×10^{ 13}\,Hz\)。
- 氢原子和碘原子之间分子键的力常数是多少?
- 当这个分子在相邻的振动能级之间过渡时,发射的光子的能量是多少?
- 回答 a
-
295 N/m
- 答案 b
-
0.277 eV
量子振荡器与传统振荡器有三个不同之处:
- 首先,量子振荡器的基态不是零。\(E_0 = \hbar \omega /2\) 在经典观点中,最低能量为零。 所有量子力学系统都普遍不存在零能态,因为海森堡不确定性原理导致无处不在的波动。 如果量子粒子一动不动地坐在电位井的底部,则其动量和位置必须同时精确,这将违反海森堡的不确定性原则。 因此,能量最低状态必须以动量和位置的不确定性为特征,因此量子粒子的基态必须位于势井的底部之上。
- 其次,可以在区间之外以非零概率找到量子谐波振荡器电位中的粒子\(-A \leq x \leq +A\)。 在问题的经典表述中,粒子不会有任何能量进入这个区域。 在经典禁区找到基态量子粒子的概率约为16%。
- 第三,处于地面低能态的量子振荡器的概率密度分布\(|\psi_n(x)|^2\)在井中间最大\((x = 0)\)。\(\psi_0(x)\) 为了使粒子在井中心以最大的概率被发现,我们预计粒子在振荡时在那里停留的时间最多。 这与传统振荡器的行为相反,在传统振荡器中,粒子的大部分时间都在转折点附近以相对较小的速度移动。
使用对称性求出处于谐波振荡器基态的粒子位置的期望值。
- 答案 b
-
\[\langle x \rangle = 0 \nonumber \]
激发态的量子概率密度分布的特征会发生变化,当量子数变高时,量子概率密度分布变得更像经典分布。 我们已经观察到量子振荡器的第一个激发态的这种变化,因为分布在转折点周围\(|\psi_1(x)|^ 2\)达到峰值,并在平衡位置消失,如图所示\(\PageIndex{2}\)。 根据玻尔的对应原理,在高量子数的极限下,谐波振荡器的量子描述与经典描述趋于一致,如图所示\(\PageIndex{3}\)。 与态的量子能量相对应的经典概率密度分布是对\(n = 12\)处于这种激发态的量子振荡器的量子概率分布的相当不错的近似值。 对于高度兴奋的州来说,这项协议变得越来越好。