7.5: 盒子里的量子粒子
- Page ID
- 202380
在本节结束时,您将能够:
- 描述如何为平稳薛定格方程设置边界值问题
- 解释为什么盒子里量子粒子的能量是量化的
- 描述薛定格方程固定解的物理含义以及这些解与随时间变化的量子态之间的联系
- 解释玻尔对应原理的物理含义
在本节中,我们将薛定格方程应用于绑定到一维盒子的粒子。 这个特殊案例为理解更复杂系统中的量子力学提供了课程。 粒子的能量是由于盒子内的驻波条件而量化的。
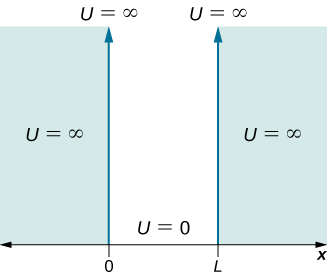
假设一个质量\(m\)粒子只能沿 x 方向移动,其运动仅限于位于和位于\(x = 0\)的硬墙和刚壁之间的区域\(x = L\)(图\(\PageIndex{1}\))。 在墙之间,粒子可以自由移动。 这种物理状况被称为无限方井,由势能函数描述
\ [U (x) =\ begin {cases}
0 & 0\ leq x\ leq L\\
\ infty & x< 0\; and\; x> L\ end {cases}\ label {3.5.2}\]
将这个方程与 Schrdinger 的时间无关波动方程相结合,可以得出
\[\dfrac{-\hbar^2}{2m} \dfrac{d^2\psi(x)}{dx^2} = E\psi(x), \, for \, 0 \leq x \leq L \label{7.32} \]
其中\(E\)是粒子的总能量。 我们期望什么类型的解决方案? 粒子的能量是一个正数,因此,如果波函数的值为正(方程的右侧),则波函数的曲率为负或向下凹面(方程的左侧)。 同样,如果波函数的值为负(方程的右侧),则波函数的曲率为正或向上凹形(方程的左侧)。 振荡波函数(例如正弦波或余弦波)满足此条件。 由于这些波浪仅限于盒子内,因此我们设想驻波的终点为\(x = 0\)和固定端点\(x = L\)。
这个\(\psi(x)\)方程的解有概率解释。 特别是,方块\(|\psi(x)|^2\)表示在特定位置 x 找到粒子的概率密度。 必须集成此函数才能确定在某个空间间隔内找到粒子的概率。 因此,我们正在寻找满足以下标准化条件的可归一化解:
\[\int_0^L dx|\psi(x)|^2 = 1. \label{7.33} \]
墙壁坚硬且无法穿透,这意味着在墙外永远找不到粒子。 从数学上讲,这意味着解必须消失在墙上:
\[\psi(0) = \psi(L) = 0. \label{7.34} \]
我们预计会有振荡解,所以这个方程最通用的解是
\[\psi_k(x) = A_k \, \cos \, kx + B_k \, \sin \, kx \label{7.35} \]
哪里\(k\)是波数,\(A_k\)和\(B_k\)是常数。 应用方程\ ref {7.33} 表示的边界条件得出
\[\psi_k(0) = A_k \, \cos (k \cdot 0) + B_k \, \sin (k \cdot 0) = A_k = 0. \label{7.36} \]
因为我们有\(A_k = 0\),所以解决方案必须是
\[\psi_k(x) = B_k \, \sin \, kx. \label{7.37} \]
如果\(B_k\)为零,则\(\psi_k(x) = 0\)无法满足所有值\(x\)和的归一化条件(方程\ ref {7.33})。 假设\(B_k \neq 0\)方程\ ref {7.34} for then 给出\(x = L\)了
\[0 = B_k \, \sin (kL) \Rightarrow \sin(kL) = 0 \Rightarrow kL = n\pi, \, n = 1,2,3,... \label{7.38} \]
我们放弃了\(n = 0\)解,因为\(\psi(x)\)这个量子数在任何地方都将为零,这是一个不可归一化的,因此是非物理的解。 用方程\ ref {7.37} 代入方程\ ref {7.32} 可以得出
\[-\dfrac{\hbar^2}{2m}\dfrac{d^2}{dx^2} (B_k \sin(kx)) = E(B_k \sin(kx)). \label{7.39} \]
计算这些导数会导致
\[E = E_k = \dfrac{\hbar^2k^2}{2m}. \label{7.40} \]
根据德布罗格利的说法\(p = \hbar k\),这个表达式意味着总能量等于动能,这与我们关于 “粒子自由移动” 的假设一致。 将方程\ ref {7.38} 和\ ref {7.40} 的结果相结合,得出
\[E_n = n^2 \dfrac{\pi^2 \hbar^2}{2mL^2}, \, n = 1,2,3,... \label{7.41} \]
方程\ ref {7.41} 认为,绑定到一维盒子的粒子只能具有某些离散(量化)的能量值。 此外,粒子的动能不能为零,绑定在盒子上的粒子不可能 “处于静止状态”。
要评估与这些能量相对应的允许波函数,我们必须找到归一化常数\(B_n\)。 我们在波函数上施加归一化条件方程\ ref {7.33}
\[\psi_n(x) = B_n \, \sin \, \dfrac{n\pi x}{L} \label{7.42} \]
我们从归一化条件开始(方程\ ref {7.33})
\[\begin{align} 1 &= \int_0^L dx|\psi_n(x)|^2 \\[5pt] &= \int_0^L dx \, B_n^2 \, \sin^2 \dfrac{n\pi}{L} x \\[5pt] &= B^2 n \int_0^2 dx \, \sin^2 \dfrac{n\pi}{L}x \\[5pt] &= B_n^2 \dfrac{L}{2} \\[5pt] \Rightarrow B_n &= \sqrt{\dfrac{2}{L}}. \end{align} \nonumber \]
因此,与方程\ ref {7.41} 中给出的能量值相对应的波函数是
\[\psi_n(x) = \sqrt{\dfrac{2}{L}} \, \sin \, \dfrac{n\pi x}{L}, \, n = 1,2,3,... \label{7.43} \]
对于最低能量状态或基态能量,我们有
\[E_1 = \dfrac{\pi^2 \hbar^2}{2mL^2}, \, \psi_1(x) = \sqrt{\dfrac{2}{L}} \, \sin \left(\dfrac{\pi x}{L}\right). \label{7.44} \]
所有其他能量状态可以表示为
\[E_n = n^2 E_1, \, \psi_n(x) = \sqrt{\dfrac{2}{L}} \, \sin \, \left(\dfrac{n\pi x}{L}\right). \label{7.45} \]
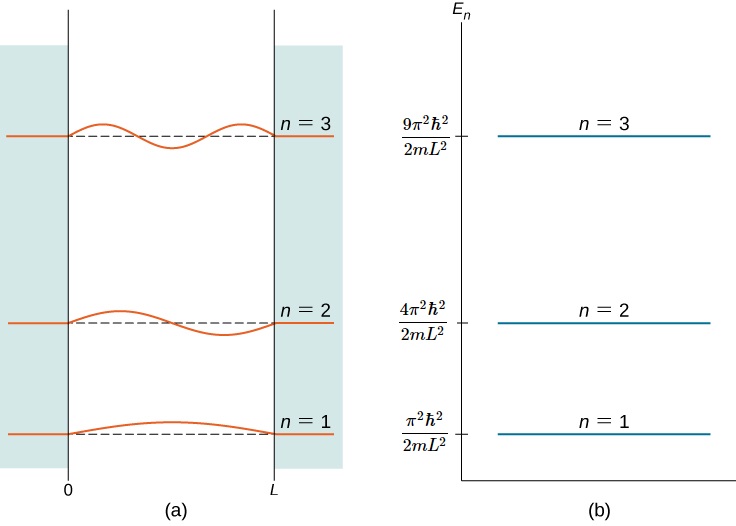
该指数被\(n\)称为能量量子数或主量子数。 的状态\(n = 2\)是第一个激发态,的状态\(n = 3\)是第二个激发态,依此类推。 框中粒子的前三个量子态(n = 1、2 和 3)如图所示\(\PageIndex{2}\)。 方程\ ref {7.45} 中的波函数有时被称为 “定能状态”。 据说处于这些状态的粒子占据能量水平,由图中的水平线表示\(\PageIndex{2}\)。 能量等级类似于梯子的梯级,粒子在获得或失去能量时可以 “攀升”。
方程\ ref {7.45} 中的波函数也称为静态和驻波态。 这些函数是 “静止的”,因为它们的概率密度函数在时间上没有变化,而 “驻波” 是因为它们的真实部分和虚构部分像驻波一样上下振荡,就像操场上两个孩子之间挥舞的绳子一样。\(|\Psi(x,t)|^2\) 平稳态是定能态(方程\ ref {7.45}),但这些状态的线性组合,例如\(\psi(x) = a\psi_1 + b\psi_2\)(也是薛定格方程的解)是混合能态。
能量量化是边界条件的结果。 如果粒子不局限在盒子里而是自由徘徊,则允许的能量是连续的。 但是,在这种情况下,只允许使用某些能量 (\(E_1, 4E_1, 9E_1,...\))。 相邻能级之间的能量差由下式给出
\[\Delta E_{n+1,n} = E_{n+1} - E_n = (n + 1)^2 E_1 - n^2E_1 = (2n + 1) E_1. \nonumber \]
节能要求,如果系统的能量发生变化,能量差将以其他形式的能量传播。 对于局限于小体积的带电粒子的特殊情况(例如,在原子中),能量变化通常会被光子带走。 发射光子的频率为我们提供了有关系统的能量差(间距)和容器体积的信息,即 “盒子” 的大小(方程\ ref {7.44})。
假设质子被限制在一个宽度的盒子内\(L = 1.00 \times 10^{-14} m\)(典型的核半径)。 地面和第一激发态的能量是多少? 如果质子从第一个激发态过渡到基态,那么发射光子的能量和频率是多少?
策略
如果我们假设限制在原子核中的质子可以建模为盒子里的量子粒子,那么我们所需要做的就是使用方程\ ref {7.41} 来找到它的能量\(E_1\)和\(E_2\)。 质子的质量是\(m = 1.76 \times 10^{-27}kg\)。 发射的光子带走了能量差\(\Delta E = E_2 - E_1\)。 我们可以使用关系\(E_f = hf\)来找出它的频率 f。
解决方案
基态:
\[\begin{align*} E_1 &= \dfrac{\pi^2 \hbar^2}{2mL^2} \\[5pt] &= \dfrac{\pi^2 (1.05 \times 10^{-34} J \cdot s)}{2(1.67 \times 10^{-27} kg)(1.00 \times 10^{-14}m)^2} \\[5pt] &= 3.28 \times 10^{−13}J \\[5pt] &= 2.05 \, MeV \end{align*} \nonumber \]
第一个激发状态:
\[E_2 = 2^2 E_1 = 4(2.05 \, MeV) = 8.20 \, MeV. \nonumber \]
发射光子的能量是
\[E_f = \Delta E = E_2 - E_1 = 8.20 \, MeV - 2.05 \, MeV = 6.15 \, MeV. \nonumber \]
发射光子的频率为
\[f = \dfrac{E_f}{h} = \dfrac{6.15 \, MeV}{4.14 \times 10^{-21}MeV \cdot s} = 1.49 \times 10^{21} Hz. \nonumber \]
意义
这是原子核发射伽玛射线的典型频率。 这个光子的能量大约是可见光光子的能量一千万倍。
粒子在盒子中的位置的期望值由下式给出
\[\langle x \rangle = \int_0^L dx \,\psi_n^* (x) x \psi_n(x) = \int_0^L dx\,x|\psi_n^*(x)|^2 = \int_0^L dx\,x \dfrac{2}{L}sin^2 \, \dfrac{nπx}{L} = \dfrac{L}{2}. \label{7.47} \]
我们还可以找到给定状态下大量粒子的动量或平均动量的期望值:
\[\begin{align} \langle p \rangle &= \int_0^L dx\psi_n^* (x) \left[-i\hbar \dfrac{d}{dx} \psi_n(x)\right] \label{7.48} \\[5pt] &= -i\hbar \int_0^L dx \sqrt{\dfrac{2}{L}} \, \sin \, \dfrac{n\pi x}{L} \left[ \dfrac{d}{dx} \sqrt{\dfrac{2}{L}} \, \sin \, \dfrac{n\pi x}{L}\right] \\[5pt] &= -i \dfrac{2\hbar}{L} \int_0^L dx \, \sin \, \dfrac{n\pi x}{L} \left[ \dfrac{n\pi}{L} \, \cos \, \dfrac{n\pi x}{L}\right] \\[5pt] &= - i\dfrac{2n\pi \hbar}{L^2} \int_0^L dx \dfrac{1}{2} \sin \, \dfrac{2n\pi x}{L} \\[5pt] &= -i \dfrac{n\pi \hbar}{L^2} \dfrac{L}{2n\pi} \int_0^{2\pi n} d\varphi \, \sin \, \varphi \\[5pt] &= -i \dfrac{\hbar}{2L} \cdot 0 \\[5pt] &= 0. \end{align} \]
因此,对于处于一定能量状态的粒子,平均位置在盒子的中间,粒子的平均动量为零,传统粒子也是如此。 请注意,虽然经典粒子的最小能量可以为零(粒子可以在盒子中间静止),但量子粒子的最小能量不是零,由方程\ ref {7.44} 给出。 第 n 个量子态中的平均粒子能量(其预期能量值)为
\[E_n = \langle E \rangle = n^2 \dfrac{\pi^2 \hbar^2}{2m}. \label{7.49} \]
结果并不奇怪,因为驻波状态是一种确定能量的状态。 该系统的任何能量测量都必须返回一个等于这些允许能量之一的值。
如果不讨论玻尔的对应原理,我们对盒子里量子粒子的分析就不完整。 该原理指出,对于大量子数,量子物理定律必须得出与经典物理定律相同的结果。 为了说明这个原理如何适用于盒子中的量子粒子,我们绘制了概率密度分布
\[|\psi_n(x)|^2 = \dfrac{2}{L} sin^2 (n\pi x/L) \label{7.50} \]
用于在粒子处于量子态时在壁\(x\)之间的位置附近寻找粒子\(\psi_n\)。 图中\(\PageIndex{3}\)显示了基态、第一激发态和对应于大量子数的高激发态的概率分布。 从这些图中我们可以看出,当量子粒子处于基态时,它很可能出现在盒子的中间,概率分布的值最大。 当粒子处于第一个激发状态时,情况并非如此,因为现在概率分布在盒子中间的值为零,因此不可能在那里找到粒子。 当量子粒子处于第一激发态时,概率分布有两个最大值,找到粒子的最佳机会是在靠近这些最大值位置的位置。 这张量子图不同于经典图片。
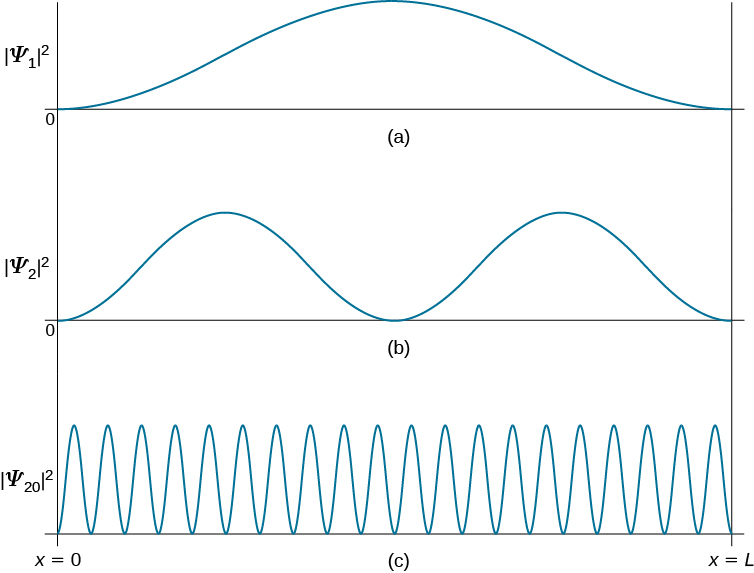
在\(x\)和之间找到经典粒子的概率密度\(x + \Delta x\)取决于粒子\(Δt\)在该区域停留的时间。 假设它的速度 u 是恒定的,那么这次是\(Δt = Δx/u\),对于墙之间的任何位置,速度也是恒定的。 因此,在整个盒子中找到经典粒子的概率密度\(x\)是均匀的,没有找到经典粒子的更好位置。 这张经典图片在大量子数的极限内相匹配。 例如,当量子粒子处于高激发态时,如图所示\(\PageIndex{3}\),概率密度以快速波动为特征,然后在区间 Δx 中找到量子粒子的概率不取决于该间隔在墙之间的位置。
一辆重达 0.40 千克的小型推车沿着两个相距 2.0 米的保险杠之间的空中轨道来回移动。 我们假设没有摩擦;与保险杠的碰撞具有很好的弹性,因此在保险杠之间,汽车保持0.50 m/s的恒定速度。将推车视为量子粒子,估计与其传统能量相对应的主量子数的值。
策略
我们发现推车的动能 K 及其基态能量就好\(E_1\)像它是一个量子粒子一样。 手推车的能量完全是动能的,所以\(K = n^2 E_1\)(方程式\ ref {7.45})。 求解 n 给出\(n = (K/E_1)^{1/2}\)。
解决方案
手推车的动能是
\[K = \dfrac{1}{2} mu^2 = \dfrac{1}{2}(0.40 \, kg)(0.50 \, m/s)^2 = 0.050 \, J. \nonumber \]
被视为量子粒子的推车的基态是
\[E_1 = \dfrac{\pi^2 \hbar^2}{2mL^2} = \dfrac{\pi^2 (1.05 \times 10^{-34} J \cdot s)^2}{2(0.40 \, kg)(2.0 \, m)^2} = 1.700 \times 10^{-68} J. \nonumber \]
因此,\[n = (K/E_1)^{1/2} = (0.050/1.700 \times 10^{-68})^{1/2} = 1.2 \times 10^{33}. \nonumber \]
意义
从这个例子中我们可以看出,经典系统的能量以非常大的量子数为特征。 玻尔的对应原则涉及这种情况。 我们可以将量子力学的形式主义应用于任何类型的系统,无论是量子系统还是经典系统,每种情况下的结果都是正确的。 在高量子数的极限下,使用量子形式主义没有任何好处,因为我们可以用传统力学中不太复杂的形式主义获得相同的结果。 但是,我们不能将经典形式主义应用于低数能态的量子系统。
(a) 考虑一口有墙壁边界的无限正方形井\(x=0\),以及\(x=L\). 在和之间的\(x=0\)某个位置找到处于基态的量子粒子的概率是\(x=L/4\)多少? (b) 对经典粒子重复问题 (a)。
解决方案
a. 9.1%;b. 25%
\(E_n\)通过求解\(ψ_n(x)\)与时间无关的 Schrdinger 方程(方程\ ref {7.32})找到了平稳态和能量之后,我们使用方程 7.4.12 来编写波函数\(Ψ_n(x,t)\),这些波函数是方程给出的随时间变化的薛定格方程的解7.4.7。 对于盒子里的粒子,这给出
\[\Psi_n(x,t) = e^{-i\omega_nt} \psi_n(x) = \sqrt{\dfrac{2}{L}}e^{-iE_nt/\hbar}sin \, \dfrac{n\pi x}{L}, \, n = 1,2,3,... \label{7.51} \]
其中能量由方程\ ref {7.41} 给出。
盒子模型中的量子粒子在一个相对较新出现的光电子学领域中有实际应用,该领域涉及将电信号转换为光信号的设备。 该模型还涉及纳米级物理现象,例如被困在以高电位屏障为界的低电势中的纳米颗粒。


