7.3: 海森堡不确定性原理
- Page ID
- 202329
在本节结束时,您将能够:
- 描述位置-动量不确定性关系的物理意义
- 解释量子理论中不确定性原理的起源
- 描述能量-时间不确定性关系的物理意义
海森堡的不确定性原理是量子力学的关键原理。 粗略地说,它指出,如果我们对粒子的位置一无所知(位置的不确定性很小),我们对其动量一无所知(动量的不确定性很大),反之亦然。 其他量也存在不确定性原理的版本,例如能量和时间。 我们分别讨论动量位置和能量时间不确定性原理。
动量和位置
为了说明动量位置不确定性原理,可以考虑一个沿 x 方向移动的自由粒子。 粒子以恒定的速度\(u\)和动量移动\(p = mu\)。 根据德布罗格利的关系,\(p = \hbar k\) 和\(E = \hbar \omega\). 如上一节所述,自由粒子的波函数由下式给出
\[ \begin{align*} \psi_k(x,t) &= A[\cos \, (\omega t - kx) - i \, \sin \, (\omega t - kx)] \\[4pt] &= A \, e^{-i(\omega t - kx)} \\[4pt] &= A \, e^{-i(\omega t - kx)} \\[4pt] &=A\, e^{-i\omega t} e^{ikx} \end{align*} \nonumber \]
而且概率密度\(|\psi_k (x,t)|^2 = A^2\)是统一的,与时间无关。 粒子同样有可能出现在 x 轴的任何地方,但具有明确的波长和波数值,因此动量值也很明确。 位置的不确定性是无限的(我们对位置完全不确定),动量的不确定性为零(我们对动量完全确定)。 这种对自由粒子的描述符合海森堡的不确定性原理。
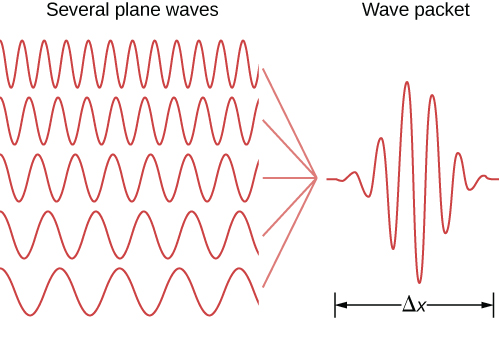
也可以对局部粒子做出类似的陈述。 在量子理论中,局部粒子是通过称为波包的自由粒子(或平面波)态的线性叠加来建模的。 波形数据包的示例如图所示\(\PageIndex{1}\)。 波包包含许多波长,因此根据德布罗格利的关系,许多瞬间——这在量子力学中是可能的! 该粒子也有许多位置值,尽管粒子主要局限于间隔内\(\Delta x\)。 如果以正确的方式将更多不同波长或力矩的平面波状态加在一起(增加),则\(\Delta x\)可以更好地定位粒子(\(\Delta p\)可以减少)。 根据海森堡的说法,这些不确定性服从以下关系。
粒子位置的不确定性及其动量不确定性的乘积决不能小于降低后的普朗克常数的一半:
\[\Delta x \Delta p \geq \dfrac{\hbar}{2}. \label{Heisen} \]
这种关系表达了海森堡的不确定性原则。 它限制了我们通过同时测量位置和动量对粒子的了解。 如果\(\Delta x\)很大,则\(\Delta p\)很小,反之亦然。 方程\ ref {Heisen} 可以在更高级的现代物理学课程中推导出来。 海森堡在他的著作《量子理论的物理原理》中反思了这种关系,他写道:“任何精度超过 [关系] 给出的精度使用'位置'和'速度'这两个词与使用意义未定义的词语一样毫无意义。”
请注意,不确定性原理与实验设备的精度无关。 即使是完美的测量设备,这些不确定性仍然存在,因为它们起源于物质的波浪状性质。 乘积的精确值\(\Delta x \Delta p\)取决于波函数的具体形式。 有趣的是,高斯函数(或钟形曲线分布)给出了不确定度乘积的最小值:
\[\Delta x \Delta p = \dfrac{\hbar}{2} \nonumber \]
如果已知以下物体的速度,则确定其位置的最小不确定性,精度\(1.0 \times 10^{-3} m/s\)为:
- 电子和
- 质量为 6.0 kg 的保龄球。
策略
鉴于速度的不确定性\(\Delta u = 1.0 \times 10^{-3} m/s\),我们必须首先确定动量的不确定性,\(\Delta p = m\Delta u\)然后反转方程\ ref {Heisen} 以找到位置的不确定性
\[\Delta x = \dfrac{\hbar}{2\Delta p}. \nonumber \]
解决方案
- 对于电子:\[\begin{align*} \Delta p &= m\Delta u \\[4pt] &= (9.1 \times 10^{-31} kg)(1.0 \times 10^{-3}m/s) \\[4pt] &= 9.1 \times 10^{-34} kg \cdot m/s,\end{align*} \nonumber \]\[\begin{align*} \Delta x &= \frac{\hbar}{2\Delta p} \\[4pt] &= 5.8 \, cm. \end{align*} \nonumber \]
- 对于保龄球:\[\begin{align*} \Delta p &= m\Delta u \\[4pt] &= (6.0 \, kg)(1.0 \times 10^{-3}m/s) \\[4pt] &= 6.0 \times 10^{-3} kg \cdot m/s, \end{align*} \nonumber \]\[\begin{align*} \Delta x &= \frac{\hbar}{2\Delta p} \\[4pt] &= 8.8 \times 10^{-33}m. \end{align*} \nonumber \]
意义
与电子的位置不确定性不同,保龄球的位置不确定性非常小。 普朗克的常数非常小,因此不确定性原理施加的限制在诸如保龄球之类的宏观系统中并不明显。
使用海森堡的不确定性原理估算氢原子的基态能量。 (提示:根据早期的实验,氢原子的大小约为0.1 nm。)
策略
绑定到氢原子的电子可以通过绑定到一维长度盒的粒子建模\(L = 0.1 \, nm\)。 该系统的基态波函数是半波。 这是盒子中可以 “适合” 的最大波长,因此波函数对应于最低能量状态。 请注意,此函数的形状与高斯(钟形曲线)函数非常相似。 我们可以把这个函数 (E) 描述的粒子的平均能量当作基态能量的良好估计值 (\(E_0\))。 粒子的平均能量与其动量平方的平均值有关,这与其动量不确定性有关。
解决方案
要解决这个问题,我们必须明确 “位置不确定性” 和 “动量不确定性” 的含义。 我们用位置的标准差 () 来识别位置的不确定性 (Δx\(σ_x\)),用动量的标准差 (\(Δp\)) 来识别动量的不确定性 (\(σ_p\))。 对于高斯函数,不确定性乘积为
\[\sigma_x\sigma_p = \frac{\hbar}{2}, \nonumber \]
哪里
\[\sigma_x^2 = x^2 - \overline{x}^2 \nonumber \]
和
\[\sigma_p^2 = p^2 - \overline{p}^2.\nonumber \]
因此,粒子向左移动的可能性与向右移动的可能性相同\(\overline{p}^2 = 0\)。 而且,位置的不确定性与盒子的大小相当,所以\(\sigma_x = L\)。 因此,估计的基态能量为
\[\begin{align*} E_0 &= E_{Gaussian} \\[4pt] &= \dfrac{\overline{p}^2}{m} \\[4pt] &= \frac{\sigma_p^2}{2m} \\[4pt] &= \frac{1}{2m} \left(\frac{\hbar}{2\sigma_x}\right)^2 \\[4pt] &= \frac{1}{2m} \left(\frac{\hbar}{2L}\right)^2 \\[4pt] &= \frac{\hbar^2}{8mL^2}. \end{align*} \nonumber \]
\[\begin{align*}E_0 &= \dfrac{(\hbar c)^2}{8(mc^2)L^2} \\[4pt] &= \frac{(197.3 \, eV \cdot nm)^2}{8(0.511 \cdot 10^6 eV)(0.1 \, nm)^2} \\[4pt] &= 0.952 \, eV \approx 1 \, eV. \end{align*} \nonumber \]
将分子和分母乘以\(c^2\)得出
意义
根据对氢原子大小的早期估计和不确定性原理,氢原子的基态能量在 eV 范围内。 电子在基态能量中的电离能约为10 eV,因此这一预测得到了大致证实。 (注意:在量子力学中进行计算时,乘积 cc 通常是一个有用的值。)
能量和时间
另一种不确定性原理涉及同时测量量子态能量及其寿命的不确定性,
\[\Delta E \Delta t \geq \frac{\hbar}{2} \label{H2} \]
哪里\(\Delta E\)是能量测量中的不确定度,\(\Delta t\)是寿命测量中的不确定度。 能量时间不确定性原理不是由方程式\ ref {Heisen} 表示的那种关系产生的,除了本文讨论之外的技术原因。 尽管如此,能量时间原理的一般含义是,仅存在很短时间的量子态不可能有确定的能量。 原因是状态的频率与时间成反比,并且频率与状态的能量相关,因此要精确地测量能量,必须对状态进行多次观测。
举例来说,以原子的激发态为例。 这些状态的有限寿命可以从原子发射光谱中观察到的光谱线的形状中推断出来。 每次激发态衰变时,发射的能量都会略有不同,因此,发射线的特征是发射光子的光谱频率(或波长)的分布。 因此,所有光谱线都以光谱宽度为特征。 发射光子的平均能量对应于激发态的理论能量,并给出了发射线峰的光谱位置。 短寿状态具有宽的光谱宽度,而长寿命状态的光谱宽度较窄。
原子通常在激发态下存在大约\(\Delta t = 10^{-8} s\)。 估计当原子从激发态过渡并同时发射平均频率为的光子时,发射光子频率的不确定性\(\Delta f\)\(f = 7.1 \times 10^{14} Hz\)。 发射的辐射是单色吗?
策略
我们反转方程\ ref {H2} 以获得能量不确定性,\(\Delta E \approx \hbar /2\Delta t\)然后将其与光子能量结合得\(E = hf\)到\(\Delta f\)。 为了估计发射是否为单色,我们进行了评估\(\Delta f/f\)。
解决方案
光子能量的扩散是\(\Delta E = h \Delta f\)。 因此,
\[\Delta E \approx \frac{\hbar}{2 \Delta t} \Rightarrow h \Delta t \approx \frac{\hbar}{2 \Delta t} \Rightarrow \Delta f \approx \frac{1}{4\pi \Delta t} = \frac{1}{4\pi (10^{-8}s)} = 8.0 \times 10^6 \, Hz, \nonumber \]
\[\frac{\Delta f}{f} = \frac{8.0 \times 10^6 \, Hz}{7.1 \times 10^{14} \, Hz} = 1.1 \times 10^{-8}. \nonumber \]
意义
由于发射的光子的频率在平均频率的\(1.1 \times 10^{-6}\)百分比之内,因此可以将发射的辐射视为单色辐射。
钠原子从第一个激发态过渡到基态,发射能量为2.105 eV的589.0纳米光子。 如果这种激发态的寿命是\(1.6 \times 10^{-8} s\),那么这种激发态的能量不确定性是多少? 相应的光谱线的宽度是多少?
- 回答
-
\(4.1 \times 10^{-8} eV\);\(1.1 \times 10^{-5} nm\)


