5.10: 相对论能量
- Page ID
- 202097
在本节结束时,您将能够:
- 解释工作能量定理是如何产生物体相对论动能的表达式的
- 展示相对论能量与经典动能的关系,并对任何有质量的物体的速度设定限制
- 描述粒子的总能量与其质量和速度有何关系
- 解释相对论与能量质量等效的关系,以及能量质量等效性的一些实际含义
图中的托卡马克\(\PageIndex{1}\)是一种实验聚变反应堆,它可以将质量转化为能量。 核反应堆证明了能量与物质之间的关系。

能量守恒是物理学中最重要的定律之一。 能量不仅有许多重要的形式,而且每种形式都可以转换为任何其他形式。 我们知道,传统上,系统中的总能量保持不变。 相对论而言,能量仍然是守恒的,但现在必须考虑能量质量等效性,例如,在核反应堆内发生的反应中。 相对论能量是故意定义的,以便它在所有惯性框架中都保持守恒,就像相对论动量一样。 因此,几个基本量以经典物理学中未知的方式相互关联。 所有这些关系都经过实验结果的验证,并产生了根本性的后果。 能源定义的改变包含了近代历史上对自然的一些最基本和最引人注目的新见解。
动能和极限速度
相对论的第一个假设指出,所有惯性框架中的物理定律都是相同的。 爱因斯坦表明,粒子的能量守恒定律在相对论上是有效的,但对于以速度和质量表示的能量,其表达方式与相对论一致。 首先考虑动能的相对论表达式。 我们再次使用 f\(u\) or velocity 将其\(v\)与观察者之间的相对速度区分开来。 通常,通过熟悉的表达方式,动能与质量和速度有关
\[K = \dfrac{1}{2} mu^2. \nonumber \]
相应的动能相对论表达式可以从工作能定理中获得。 这个定理指出,系统上的网络工作转化为动能。 具体来说,如果是力,表示为
\[\vec{F} = \dfrac{d\vec{p}}{dt} = m\dfrac{d(\gamma \vec{u})}{dt} \nonumber \]
将粒子从静止状态加速到最终速度,对粒子所做的工作应等于其最终动能。 在数学形式中,对于一维运动:
\[\begin{align*} K &= \int Fdx = \int m \dfrac{d}{dt} (\gamma u) dx \nonumber \\[4pt] &= m \int \dfrac{d(\gamma u)}{dt} \dfrac{dx}{dt} \\[4pt] &= m \int u \dfrac{d}{dt} \left( \dfrac{u}{\sqrt{1 - (u/c)^2}}\right) dt. \end{align*} \nonumber \]
将其@@ 按零件集成即可获得
\[\begin{align*} K &= \left. \dfrac{mu^2}{\sqrt{1 - (u/c)^2}}\right|_{0}^{u} - m\int \dfrac{u}{\sqrt{1 - (u/c)^2}}\dfrac{du}{dt}dt \\[4pt] &= \dfrac{mu^2}{\sqrt{1 - (u/c)^2}} - m\int \dfrac{u}{\sqrt{1 - (u/c)^2}}du \\[4pt] &= \left. \dfrac{mu^2}{\sqrt{1 - (u/c)^2}} - mc^2 (\sqrt{1 - (u/c)^2})\right|_0^u \\[4pt] &= \dfrac{mu^2}{\sqrt{1 - (u/c)^2}} + \dfrac{mu^2}{\sqrt{1 - (u/c)^2}} - m c^2 \\[4pt] &= mc^2 \left[ \dfrac{(u^2/c^2) + 1 - (u^2/c^2)}{\sqrt{1 - (u/c)^2}}\right] - mc^2 \nonumber \\[4pt] &= \dfrac{mc^2}{\sqrt{1 - (u/c)^2}} - mc^2. \end{align*} \nonumber \]
因此,任何质量粒子的相对论动能都\(m\)是
\[K_{rel} = (\gamma - 1)mc^2. \label{RKE} \]
当一个物体一动不动时,它的速度是\(u = 0\)和
\[\gamma = \dfrac{1}{\sqrt{1 - \dfrac{u^2}{c^2}}} = 1 \nonumber \]
这样\(K_{rel} = 0\)就可以像预期的那样静止了。 但是,相对论动能(例如总能量和静止能)的表达方式看起来并不像经典的表达方式\(\dfrac{1}{2} mu^2\)。 为了表明 for 的表达式\(K_{rel}\)简化为低速动能的经典表达式,我们使用二项式展开来获得小值的\((1 + ε)^n\)近似值\(ε\):
\[(1 + ε)^n = 1 + nε + \dfrac{n(n−1)}{2!}ε^2 + \dfrac{n(n−1)(n−2)}{3!}ε^3 +⋯ ≈ 1 + nε \nonumber \]
忽略了非常小的术语\(ε^2\)和更高的权力\(ε\)。 选择\(ε = −u^2/c^2\)并\(n = -\dfrac{1}{2}\)得出这样的结论:\(\gamma\)在非相对论的速度下,哪里\(ε = u/c\)很小,就能满足
\[\gamma = (1 - u^2/c^2)^{-1/2} \approx 1 + \dfrac{1}{2} \left( \dfrac{u^2}{c^2}\right). \nonumber \]
二项式展开是一种将代数量表示为无限序列项之和的方法。 在某些情况下,例如这里的小速度极限,大多数术语都很小。 因此,此处导出的表达式并不精确,但它是一个非常准确的近似值。\(\gamma\) 因此,在低速时:
\[\gamma - 1 \approx \dfrac{1}{2} \left(\dfrac{u^2}{c^2}\right). \nonumber \]
在相对论动能表达式(方程\ ref {RKE})中输入这个可以得出
\[\begin{align*} K_{rel} &\approx \left[\dfrac{1}{2}\left( \dfrac{u^2}{c^2}\right)\right] mc^2 \\[4pt] &\approx \dfrac{1}{2} mu^2 \\[4pt] &\approx K_{class}. \end{align*} \nonumber \]
也就是说,相对论动能在什么时候变得与传统动能相同\(u \ll c\)。
更有趣的是,研究当物体的速度接近光速时动能会发生什么。 我们知道,\(\gamma\)随着速度的\(u\)临近\(c\),它会变得无限,所以随着速度接近光速,它\(K_{rel}\)也会变得无限(图\(\PageIndex{2}\))。 \(K_{class}\)随着\(v\)临近\(K_{rel}\),增长幅度远大于增加量\(c\)。 要将质量加速到光速,需要无限量的工作(因此也需要无限量的能量输入)。
任何有质量的物体都无法达到光速。
光速是任何具有质量的粒子的最终速度极限。 所有这些都与以下事实一致,即小于 c 的速度加起来总是小于\(c\)。 动能的相对论形式和极限速度都\(c\)已在许多实验中得到详细证实。 无论为加速质量投入多少能量,它的速度都只能接近光速,而不能达到光速。
电子有速度\(v = 0.990 c\)。
- 计算电子的动能(以兆电子伏为单位)。
- 将其与该速度下动能的经典值进行比较。 (电子的质量为\(9.11 \times 10^{-31}kg\)。)
策略
相对论动能的表达式总是正确的,但对于 (a),必须使用它,因为速度高度相对论(接近\(c\))。 首先,我们计算相对论因子\(\gamma\),然后用它来确定相对论动能。 对于 (b),我们计算了经典动能(如果小于百分之几\(v\),则接近相对论值\(c\)),然后发现它不一样。
(a) 的解决方案
- 找出已知数:\(v = 0.990c\);\(m = 9.11 \times 10^{-31}kg\)
- 识别未知事物:\(K_{rel}\).
- 将答案表示为方程式:\(K_{rel} = (\gamma - 1)mc^2\)与\(\gamma = \dfrac{1}{\sqrt{1 - u^2/c^2}}.\)
- 进行计算。 首先计算\(\gamma\)。 保留额外的数字,因为这是中间计算:\[\begin{align*} \gamma &= \dfrac{1}{\sqrt{1 - u^2/c^2}} \nonumber \\[4pt] &= \dfrac{1}{\sqrt{1 - \dfrac{(0.990c)^2}{c^2}}} \nonumber \\[4pt] &= 7.0888. \end{align*} \nonumber \]现在使用这个值来计算动能(方程\ ref {RKE}):
\[\begin{align*} K_{rel} &= (\gamma - 1)mc^2 \nonumber \\[4pt] &= (7.0888 - 1)(9.11 \times 10^{-31}\, kg)(3.00 \times 10^8\, m/s^2) \nonumber \\[4pt] &= 4.9922 \times 10^{−13}\, J \end{align*} \nonumber \]
- 转换单位:
\[\begin{align*} K_{rel} &= (4.9922 \times 10^{−13}\, J) \left(\dfrac{1\, MeV}{1.60 \times 10^{−13} J}\right) \\[4pt] &= 3.12\, MeV.\end{align*} \nonumber \]
(b) 的解决方案
- 列出已知数:\(v = 0.990c\);\(m = 9.11 \times 10^{−31}kg\).
- 列出未知的:\(K_{rel}\)
- 将答案表示为方程式:
- 进行计算:
\[\begin{align*} K_{class} &= \dfrac{1}{2} mu^2 \\[4pt] &= \dfrac{1}{2} (9.11 \times 10^{-31} kg)(0.990)^2(3.00 \times 10^8\, m/s)^2 \\[4pt] &= 4.0179 \times 10^{−14}J.\end{align*} \nonumber \]
- 转换单位:
\[\begin{align*} K_{class} &= 4.0179 \times 10^{-14} J \left(\dfrac{1\, MeV}{1.60 \times 10^{-13} J}\right) \\[4pt] &= 0.251\, MeV.\end{align*} \nonumber \]
意义
不出所料,由于速度为光速的99.0%,因此经典动能与正确的相对论值有很大不同。 另请注意,经典值比相对论值小得多。 实际上,\(K_{rel}/K_{class} = 12.4\)在这种情况下。 这说明了要让质量移动到接近光速的速度是多么困难。 需要的能量比传统预测的要多得多。 要使质量的速度更接近光的速度,需要不断增加的能量。 对于电子来说,3 兆电子伏的能量非常小,它可以通过当今的粒子加速器来实现。 例如,SLAC 可以将电子加速到结束\(50 \times 10^9 eV = 50,000\, MeV\)。
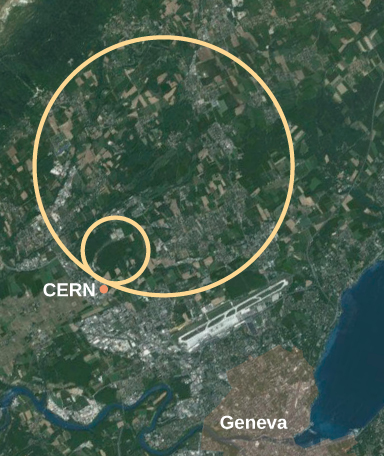
让 v 比 99.0% 或 99.9% 更接近 c 有什么意义吗? 答案是肯定的。 通过这样做,我们可以学到很多东西。 进入高速质量的能量可以转化为任何其他形式,包括转化为全新的粒子。 在图中的大型强子对撞机中\(\PageIndex{1}\),带电粒子在进入环状结构之前会被加速。 在那里,两束粒子被加速到它们的最终速度,大约是相反方向光速的99.7%,然后发生碰撞,产生全新的粒子种类。 我们所知道的关于物质的子结构和自然界中奇异的短寿命粒子收集的大部分知识都是通过这种方式学习的。 这些以前未知的粒子的特性模式暗示着所有物质的基本子结构。 这些粒子及其某些特性将在后面的粒子物理学章节中讨论。
总相对论能量
动能的表达式可以重新排列为:
\[\begin{align*} E &= \dfrac{mc^2}{\sqrt{1 - u^2/c^2}} \\[4pt] &= K + mc^2. \end{align*} \nonumber \]
爱因斯坦在后来也发表于1905年的另一篇文章中指出,如果粒子的能量发生变化\(\Delta E\),其质量就会改变\(\Delta m = \Delta E/C^2\)。 自那时以来,大量实验证据证实,这与质量粒子静\(m\)止时的能量\(mc^2\)相对应。 例如,当静止状态的中性质子分解成两个光子\(m\)时,光子的质量为零,但观察到的总能量与介子的总能量相对应。\(mc^2\) 同样,当质量粒子分\(m\)解成两个或更多总质量较小的粒子时,观测到的赋予衰变产物的动能与质量的减少相对应。 因此,\(E\)是粒子的总相对论能量,\(mc^2\)也是其静止能量。
粒子的@@ 总能量 (\(E\)) 为
\[E = \gamma mc^2 \nonumber \]
其中\(m\)是质量,\(c\)是光速\(\gamma = \dfrac{1}{\sqrt{1 - \dfrac{u^2}{c^2}}}\),\(u\)是质量相对于观察者的速度。
物体的@@ 静止能量是
\[E_0 = mc^2. \label{rest energy} \]
方程\ ref {rest energy} 是爱因斯坦最著名的方程的正确形式,它首次表明能量与静止物体的质量有关。 例如,如果能量存储在物体中,则其静止质量会增加。 这也意味着可以摧毁质量以释放能量。 前两个方程对相对论能量的含义如此广泛,以至于在爱因斯坦于1905年发表它们之后的几年里,它们没有被完全认可,起初它们是正确的实验证据也没有得到广泛认可。 应该注意的是,爱因斯坦确实理解并描述了他的理论的含义和含义。
计算 1.00g 质量的剩余能量。
策略
一克是小质量——不到一分钱质量的一半。 我们可以将这个质量(单位为 SI)乘以光速的平方,得出等效的剩余能量。
解决方案
- 找出已知数:\(m = 1.00 \times 10^{-3} kg\);\(c = 3.00 \times 10^8 m/s\).
- 识别未知事物:\(E_0\).
- 将答案表示为方程式:\(E_0 = mc^2\).
- 进行计算:
\[E_0 = mc^2 = (1.00 \times 10^{-3} kg) (3.00 \times 10^8 m/s)^2 = 9.00 \times 10^{13} kg \cdot m^2/s^2. \nonumber \]
- 转换单位。 请注意\(1\, kg \cdot m^2/s^2 = 1\, J\),我们看到剩下的能量是:
\[E_0 = 9.00 \times 10^{13}\, J. \nonumber \]
意义
对于 1.00 g 的质量来说,这是一笔巨大的能量。 静止能量之所以大,是因为光速 c 是一个很大的数字,而且\(c^2\)是一个非常大的数字,所以对于任何宏观质量来说,这\(mc^2\)都是巨大的。 1.00 g 的\(9.00 \times 10^{13} J\)剩余质量能量大约是广岛原子弹释放的能量的两倍,大约是大型航空母舰动能的 10,000 倍。
今天,将质量转化为另一种形式的能量,例如在核武器和核电厂中的实际应用已广为人知。 但是,当爱因斯坦首次提出相对论能量的正确形式时,也存在一些例子,他确实描述了其中的一些。 核辐射是在过去十年中发现的,其能量来源一直是个谜。 解释是,在某些核过程中,核辐射会摧毁少量物质,释放和携带能量。 但是销毁的数量如此之少,以至于很难发现是否有任何丢失。 尽管爱因斯坦提议将其作为当时正在研究的放射性盐中的能量来源,但许多年后,人们才普遍认识到质量可以转化为能量,而且实际上通常会转化为能量(图\(\PageIndex{4}\))。

由于静止能量与质量的关系,我们现在将质量视为一种能量形式,而不是一种单独的东西。 在爱因斯坦创作之前,甚至没有任何暗示。 现在,众所周知,能量质量等效性是太阳的能量来源,核衰变的能量,甚至是保持地球内部高温的能量来源之一。
储存的能量和势能
静止物体中储存的能量会怎样,例如通过充电进入电池的能量,或者储存在玩具枪压缩弹簧中的能量? 能量输入成为物体总能量的一部分,从而增加其静止质量。 所有存储的能量和势能在系统中变成质量。 看似矛盾的是,质量守恒原理(意思是总质量恒定)是十九世纪科学证实的伟大定律之一。 为什么没有发现它不正确? 以下示例有助于回答这个问题。
汽车电池的额定电压为 12.0 V 时能够移动 600 安培小时\((A \cdot h)\)的电量
- 假设没有任何化学反应物进入或离开电池,计算这种电池从完全耗尽到充满电后的剩余质量的增加。
- 鉴于电池的重量为20.0 kg,这增加了多少百分比?
策略
在(a)部分中,我们首先必须找到以化学能形式存储在电池\(E_{batt}\)中的能量,这等于电池可以提供的电能。 因为\(E_{batt} = qV\),我们必须计算电荷\(q\)输入\(600\, A \cdot h\),这是电流\(I\)和时间的乘积\(t\)。 然后我们将结果乘以 12.0 V。然后我们可以使用以下方法计算电池质量的增加\(E_{batt} = (\Delta m)c^2\)。 第 (b) 部分是转换为百分比的简单比率。
(a) 的解决方案
- 识别已知数:\[I \cdot t = 600\, A \cdot h;\, V = 12.0\, V;\, c = 3.00 \times 10^8\, m/s. \nonumber \]
- 识别未知事物:\(\Delta m\).
- 将答案表示为方程式:\[\begin{align*} E_{batt} &= (\Delta m)c^2 \\[4pt] \Delta m &= \dfrac{E_{batt}}{c^2} \\[4pt] &= \dfrac{qV}{c^2} \\[4pt] &= \dfrac{(It)V}{c^2}.\end{align*} \nonumber \]
- 进行计算:\[\Delta m = \dfrac{(600\, A \cdot h)(12.0\, V)}{(3.00 \times 10^8)^2}. \nonumber \]
- 将安培 A 写为库仑每秒 (C/s),并将小时转换为秒:
\[\begin{align*}\Delta m &= \dfrac{(600\, C/s \cdot h)\left(\dfrac{3600\, s}{1\, h}\right)(12.0\, J/C)}{(3.00 \times 10^8\, m/s)^2} \\[4pt] &= 2.88 \times 10^{-10}\, kg. \end{align*} \nonumber \]
我们在哪里使用了转换\(1\, kg \cdot m^2/s^2 = 1\, J.\)。
(b) 的解决方案
对于 (b) 部分:
- 找出已知数:\(\delta m = 2.88 \times 10^{-10}kg\);\(m = 20.0\, kg\).
- 识别未知的:百分比变化。
- 将答案表示为方程式:\[\%\, increase = \dfrac{\delta m}{m} \times 100\%. \nonumber \]
- 进行计算:
\[\begin{align*} \%\, increase &= \dfrac{\Delta m}{m} \times 100\% \\[4pt] &= \dfrac{2.88 \times 10^{-10}\, kg}{20.0\, kg} \times 100\% \\[4pt] &= 1.44 \times 10^{-9} \% \end{align*} \nonumber \]
意义
质量的实际增加和增加的百分比都很小,因为能量除以\(c^2\)一个非常大的数字。 我们必须能够将电池的质量精度测量到十亿分之一百分点或百分之一的精度\(10^{11}\),才能注意到这种增加。 难怪不容易观察到质量变化。 实际上,这种质量的变化非常小,以至于我们可能会质疑有人怎么能证实它是真实的。 答案是在核过程中找到的,在这个过程中,大规模毁灭的百分比足够大,可以精确测量。 例如,在使用核反应堆的能量时,其燃料的质量要小得多。 在这种情况下,储存的能量已被释放(主要转化为热能为发电机供电),其余质量减少了。 使用电池中储存的能量也会减少质量,唯一的不同是核过程中储存的能量要大得多,这使得质量的变化在实践和理论上都是可以测量的。
相对论能量和动量
我们传统上知道动能和动量是相互关联的,因为:
\[K_{class} = \dfrac{p^2}{2m} = \dfrac{(mu)^2}{2m} = \dfrac{1}{2}mu^2. \nonumber \]
相对论上,我们可以通过代数操纵能量和动量的定义方程来获得能量和动量之间的关系。 这会产生:
\[E^2 = (pc)^2 + (mc^2)^2, \label{5.11} \]
相对论\(E\)的总能量在哪里,
\[E = \dfrac{mc^2 }{\sqrt{1 - u^2/c^2}} \nonumber \]
并且\(p\)是相对论的动量。 相对论能量和相对论动量之间的这种关系比经典版本更为复杂,但是我们可以通过研究获得一些有趣的新见解。 首先,总能量与动量和静止质量有关。 静止时,动量为零,方程将总能量定为剩余能量\(mc^2\)(因此此方程与上面关于静止能量的讨论一致)。 但是,随着质量的加速,其动量\(p\)会增加,从而增加总能量。 在足够高的速度下,剩余能量项与动量项相比\((mc^2)^2\)变得可以忽略不计\((pc)^2\);因此,\(E = pc\)在极其相对论的速度下。
如果我们认为\(p\)动量与质量不同,我们可以确定方程的含义
\[E^2 = (pc)^2 + (mc^2)^2, \nonumber \]
对于没有质量的粒子。 如果我们在这个方程中取\(m\)为零,那么\(E = pc,\, orp = E/c\)。 无质量粒子有这种动量。 自然界中有几种无质量粒子,包括光子(电磁辐射包)。 另一个含义是,无质量粒子必须以 c 的速度传播,并且只能以 c 的速度传播。 详细研究方程中的关系超出了本文的范围,但是你可以看到这种关系\(E^2 = (pc)^2 + (mc^2)^2\)在狭义相对论中具有重要的意义。
如果电子的速度是,那么它的动能是\(0.992c\)多少?
- 回答
-
\[ \begin{align*} K_{rel} &= (\gamma - 1)mc^2 = \left(\dfrac{1}{\sqrt{1 - \dfrac{u^2}{c^2}}} - 1 \right) mc^2 \nonumber \\[4pt] &= \left(\dfrac{1}{\sqrt{1 - \dfrac{(0.992 c)^2}{c^2}}} - 1 \right) (9.11 \times 10^{-31}\, kg)(3.00 \times 10^8\, m/s)^2 \nonumber \\[4pt] &= 5.67 \times 10^{-13}\, J \end{align*} \nonumber \]


