5.9: 相对论动量
- Page ID
- 202136
在本节结束时,您将能够:
- 用质量和速度定义相对论动量
- 展示相对论动量与经典动量有何关系
- 展示相对论动量守恒如何将质量的物体限制为小于 c 的速度
动量是物理学的核心概念。 牛顿第二定律的最广泛形式是用动量表示的。 每当系统上的净外力为零时,动量就保持不变。 这使得动量守恒成为分析碰撞的基本工具(图\(\PageIndex{1}\))。 我们对亚原子结构的了解大部分来自对加速器产生的相对论粒子碰撞的分析,而动量守恒在这项分析中起着至关重要的作用。

相对论的第一个假设指出,所有惯性框架中的物理定律都是相同的。 动量守恒定律能否在高速下满足这一要求? 可以证明,仅计算出的动量\(\vec{p} = m\frac{d\vec{x}}{dt}\),即使在一个参考系中是守恒的,在将洛伦兹变换应用于速度之后,在另一个参考系中也可能无法守恒。 相反,正确的动量方程可以看作是在粒子的静止帧中观察到的粒子正确时间的增量 d 的经典表达式:
\[\begin{align*} \vec{p} &= m\frac{d\vec{x}}{dτ} = m\frac{d\vec{x}}{dt} \frac{dt}{d\tau} \\[5pt] &= m\frac{d\vec{x}}{dt}\frac{1}{\sqrt{1 - u^2/c^2}} \\[5pt] &= \frac{m\vec{u}}{\sqrt{1 - u^2/c^2}} \\[5pt] &= \gamma m\vec{u}.\end{align*} \nonumber \]
相对论动量\(\vec{p}\)是经典动量乘以相对论因子\(\gamma\):
\[\vec{p} = \gamma m\vec{u} \label{Rmomentum} \]
其中\(m\)是物体的剩余质量,\(\vec{u}\)是其相对于观察者的速度,\(γ\)是相对论因子:
\[\gamma = \frac{1}{\sqrt{1 - \frac{u^2}{c^2}}}. \label{Rmass} \]
请注意,我们在此\(u\)处使用速度来将其\(v\)与观察者之间的相对速度区分开来。 这里\(\gamma\)出现的因子与之前的相对论因子具有相同的形式,唯一的\(\gamma\)不同是它现在是以粒子的速度\(u\)而不是两个参考系的相对速度 v 表示的。
以这种方式表示 p 时,只要净外力为零,总动量\(p_{tot}\)就是守恒的,就像在经典物理学中一样。 我们再次看到,相对论量与低速下的经典量几乎相同,后者\(u/c\)\(\gamma\)很小,几乎等于 1。 相对论动量与传统动量具有相同的直观作用。 对于高速移动的大质量来说,它最大,但由于这个因素\(\gamma\),相对论动量随着\(u\)临近而接近无穷大\(c\)(图\(\PageIndex{2}\))。 这再次表明有质量的物体无法达到光速。 如果是这样,它的势头就会变得无限——这是一个不合理的价值。
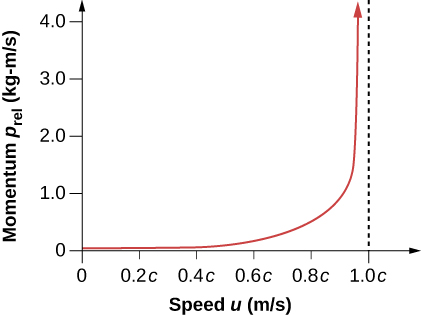
相对正确的动量定义(方程\ ref {Rmomentum})有时被认为意味着质量随速度而变化:\(m_{var} = \gamma m\)尤其是在较旧的教科书中。 但是,请注意,\(m\)这是静止人员测量的物体相对于物体的质量。 因此,\(m\)被定义为静止质量,可以在静止时测量,可能使用重力。 当质量相对于观察者移动时,确定其质量的唯一方法是通过碰撞或其他涉及动量的方法。 由于无法独立于动量来确定移动物体的质量,因此唯一有意义的质量是静止质量。 因此,当我们使用 “质量” 一词时,假设它与 “静止质量” 相同。
相对论动量的定义方式是,动量守恒在所有惯性框架中都保持不变。 每当系统上的净外力为零时,相对论动量就是守恒的,就像传统动量一样。 这已经在许多实验中得到证实。
电子以一定速度行进的动量是多\(0.985c\)少? 电子的剩余质量是\(9.11 \times 10^{-31} kg\)。
- 回答
-
将数据替换为方程\ ref {Rmomentum}:
\[\begin{align*} p &= \gamma mu \\[5pt] &= \frac{mu}{\sqrt{1 - \frac{u^2}{c^2}}} \\[5pt] &= \frac{(9.11 \times 10^{-31}kg)(0.985)(3.00 \times 10^8 \, m/s)}{\sqrt{1 - \frac{(0.985c)^2}{c^2}}} \\[5pt] &= 1.56 \times 10^{-21} \, kg-m/s. \end{align*} \nonumber \]


