5.8: 光的多普勒效应

Last updated
Save as PDF

Page ID: 202112

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

学习目标

在本节结束时，您将能够：

解释当观察者和光源相互移向或远离时，观测波长的频率和波长偏移的起源
推导出相对论多普勒位移的表达式
将多普勒移位方程应用于真实示例

正如在关于声音的章节中所讨论的那样，如果声源和听众之间的距离越来越远，则听众每秒遇到的波浪周期要比它们的分离保持恒定时更少，因此频率更低。出于同样的原因，如果源和听者越来越近，则监听器会检测到更高的频率。由此产生的检测频率的多普勒偏移发生在任何形式的波浪中。但是，对于声波，多普勒移位的方程明显不同，具体取决于运动的是声源、观察者还是空气。光不需要介质，光在真空中传播的多普勒偏移仅取决于观察者和光源的相对速度。

相对论多普勒效应

假设里面的观察者在快速\(S'\)移开时\(S\)看到来自光源的光\(v\)（图\(\PageIndex{1}\)）。光的波长可以在内部\(S'\)进行测量，例如，使用镜子设置驻波并测量节点之间的距离。这些距离是合适的长度，以其静止帧\(S'\)为准，在观察者的框架中测量\(\sqrt{1 - v^2/c^2}\)时会按一个系数变化\(S\)，其中测量波长的标尺\(S'\)被视为移动。

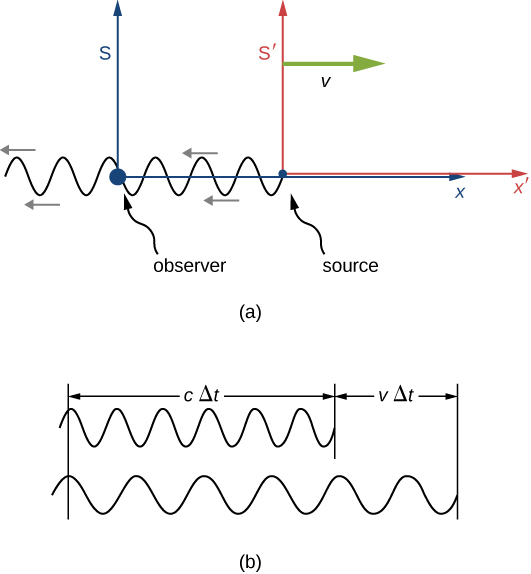
在图 a 中：观察者显示在静止帧 S 的原点处。S 素帧以相对于帧 S 的速度 v 向右移动。S 素数原点的源发出向左传播的正弦波。在图 b 中，六个波浪周期显示了观察者看到的波浪周期和源头看到的波浪周期。观察者看到的波长的长度比光源看到的波长长。从源头看到的六个循环的宽度被标记为 c delta t。观察者看到的六个周期结束时的额外长度被标记为 v delta t。 — 图\(\PageIndex{1}\)：(a) 当固定在移动惯性框架 S 中的光源发射光波时，S 中的观察者会看到以 S'. 测量的波长短了一个系数\(\sqrt{1 - v^2/c^2}\)。 (b) 由于观察者看到源在 S 内移动，因此在 S 中到达观察者的波浪模式也会被因子拉伸\((c\Delta t + v\Delta t)/(c\Delta t) = 1 + v/c\)。

如果声源在 S 中处于静止状态，则观察者将在时间 Δt 中看到波浪图案的长度 CαT。但是由于 S 相对于 S 的运动（仅在 S 内考虑），观察者会看到波浪图案，因此波长延伸了一倍

\[\frac{c\Delta t_{period} + v\Delta t_{period}}{c\Delta t_{period}} = 1 + \frac{v}{c} \nonumber \]

如图 (b) 所示\(\PageIndex{1}\)。两种效果的总体增加可以得到

\[\begin{align*} \lambda_{obs} &= \lambda_{src} \left(1 + \frac{v}{c}\right) \sqrt{\frac{1}{1 - \frac{v^2}{c^2}}} \\[4pt] &= \lambda_{src} \left(1 + \frac{v}{c}\right) \sqrt{\frac{1}{\left(1 + \frac{v}{c}\right) \left(1 - \frac{v}{c}\right)}} \\[4pt] &= \lambda_{src}\sqrt{\frac{\left(1 + \frac{v}{c}\right)}{\left(1 - \frac{v}{c}\right)}} \end{align*} \nonumber \]

其中\(\lambda_{src}\)是光源在 S 中看到的光的波长，\(\lambda_{obs}\)是观察者在 S 范围内检测到的波长。

红移和蓝移

观测到\(λ_{obs}\)的电磁辐射波长（称为 “红移”）比光源远离观察者时发射的波长长。同样，当光源向观察者移动时，波长会变短（称为 “蓝移”）。变化金额由以下因素决定

\[\lambda_{obs} = \lambda_s \sqrt{\frac{\left(1 + \frac{v}{c}\right)}{\left(1 - \frac{v}{c}\right)}} \nonumber \]

其中\(\lambda_s\)是源参考系中的波长，\(v\)是两个帧的相对速度\(S\)和\(S'\)。对于远离观察者的运动，速度\(v\)为正值，对于向观察者运动，速度为负值。就源频率和观测频率而言，这个方程可以写成

\[ f_{obs} = f_s \sqrt{\frac{\left(1 - \frac{v}{c}\right)}{\left(1 + \frac{v}{c}\right)}} \label{eq20} \]

请注意，这些符号与波长方程的符号不同。

示例\(\PageIndex{1}\): Calculating a Doppler Shift

假设一个星系正以 0.825 c 的速度离开地球。它发射波长为的无线电波

0.525 m。我们将在地球上探测到什么波长？

策略

由于星系以相对论的速度移动，因此我们必须使用相对论的多普勒移位而不是传统的多普勒移位来确定无线电波的多普勒偏移。

解决方案

识别已知数:\(u = 0.825 c\);\(\lambda_s = 0.525 \, m\).
识别未知事物:\(\lambda_{obs}\).
将答案表示为方程式：
\[\lambda_{obs} = \lambda_s \sqrt{\frac{1 + \frac{v}{c}}{1 - \frac{v}{c}}}. \nonumber \]
进行计算：
\[\begin{align*}\lambda_{obs} &= \lambda_s \sqrt{\frac{1 + \frac{v}{c}}{1 - \frac{v}{c}}} \\[4pt] &= (0.525 \, m) \sqrt{\frac{1 + \frac{0.825c}{c}}{1 - \frac{0.825c}{c}}} \\[4pt] &= 1.70 \, m. \end{align*} \nonumber \]

意义

由于星系正在远离地球，我们预计它发出的辐射波长会被红移。我们计算的波长为 1.70 m，与原始波长 0.525 m 相比红移。你将在《粒子物理学》和《宇宙学》中看到，探测红移辐射可以让当今人们了解宇宙的起源和演变。

练习\(\PageIndex{1}\)

假设太空探测器以 0.350 c 的速度离开地球。它以 1.50 GHz 的频率将无线电波信息发送回地球。地球上收到信息的频率是多少？

解决方案

我们可以将数据直接替换到相对论多普勒频率的方程中（方程\ ref {eq20}）：

\[\begin{align*}f_{obs} &= f_s \sqrt{\frac{1 - \frac{v}{c}}{1 + \frac{v}{c}}} \\[4pt] &= (1.50 \, GHz)\sqrt{\frac{1 - \frac{0.350c}{c}}{1 + \frac{0.350c}{c}}} \\[4pt] &= 1.04 \, GHz. \end{align*} \nonumber \]

相对论的多普勒效应的应用范围从多普勒雷达风暴监测到提供有关恒星运动和距离的信息。我们在练习中描述了其中的一些应用程序。