5.7: 相对论速度变换
- Page ID
- 202113
在本节结束时,您将能够:
- 推导出与狭义相对论一致的方程,用于将一个惯性参考系中的速度转换为另一个惯性参考系中的速度。
- 将速度变换方程应用于以相对论速度移动的物体。
- 研究相对论变换方程预测的组合速度与经典预期的速度相比如何。
在快速移动的河流中,在皮划艇上保持原位需要付出努力。 河流拉动皮划艇前进。 尝试在水流中划桨可以使皮划艇相对于水向上游移动,但这仅占其相对于海岸速度的一部分。 皮划艇的运动是牛顿力学中的速度如何通过向量加法结合在一起的一个例子。 皮划艇的速度是其相对于水的速度和水相对于河岸的速度的矢量和。 但是,速度的相对论加法却大不相同。
速度变换
想象一下,一辆汽车在夜间沿着直路行驶,如图所示\(\PageIndex{1}\)。 驾驶员看见灯光在汽车的参照\(c\)范围内高速离开大灯。 如果伽利略变换应用于光,那么汽车大灯发出的光将以一定的速度接近行人\(u = v + c\),这与爱因斯坦的假设相反。
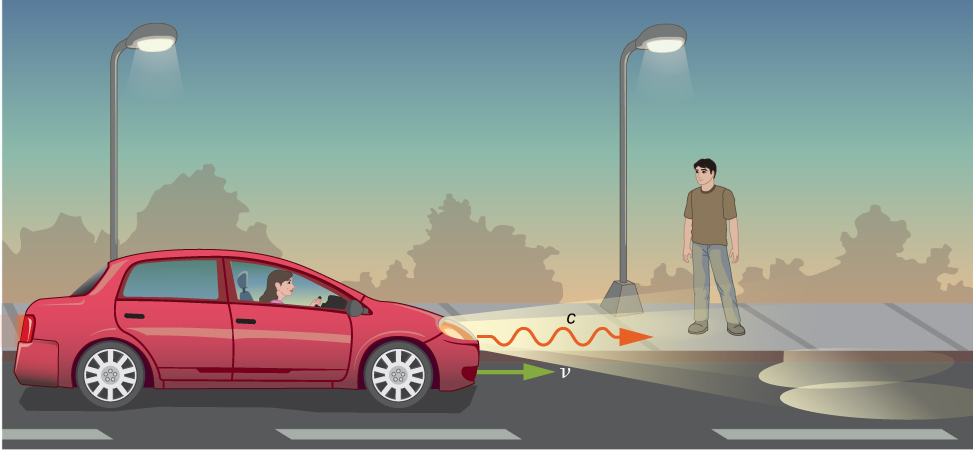
在两个参照系中,行进距离和行进时间都是不同的,它们必须有所不同,使所有惯性系中的光速相同。 将速度从一帧转换到另一帧的正确规则可以从洛伦兹变换方程中获得。
速度的相对论变换
假设物体 P 正在以\(S'\)帧中测量\(u = (u'_x, u'_y, u'_z)\)的恒定速度移动。 \(S'\)帧正沿着其 x 轴以速度移动\(v\)。 以时间 dt' 为增量,粒子\(dx'\)沿 x'-轴移动。 应用洛伦兹变换方程可以得出未底数轴上相应的时间和位移增量:
\[\begin{align} dt &= \gamma (dt' + vdx' /c^2) \\[4pt] dx &= \gamma (dx' + vdt') \\[4pt] dy &= dy' \\[4pt] dz &= dz'. \end{align} \nonumber \]
然后,在未填充坐标系中看到的粒子的速度分量是
\[\begin{align} \dfrac{dx}{dt} &= \dfrac{\gamma(dx' + vdt')}{\gamma (dt' + v\,dx'/c^2)} = \dfrac{\dfrac{dx'}{dt'} + v}{1 + \dfrac{v}{c^2} \dfrac{dx'}{dt'}} \\[4pt] \dfrac{dy}{dt} &= \dfrac{dy'}{\gamma (dt' + v\,dx'/c^2)} = \dfrac{\dfrac{dy'}{dt'}}{\gamma \left(1 + \dfrac{v}{c^2} \dfrac{dx'}{dt'}\right)} \\[4pt] \dfrac{dz}{dt} &= \dfrac{dz'}{\gamma (dt' + v\,dx'/c^2)} = \dfrac{\dfrac{dz'}{dt'}}{\gamma \left(1 + \dfrac{v}{c^2} \dfrac{dx'}{dt'}\right)} \end{align} \nonumber \]
因此,我们得出了物体速度分量的方程式,如帧所示\(S\):
\[u_x = \left(\dfrac{u'_x + v}{1 + vu'_x/c^2}\right), \, u_y = \left(\dfrac{u'_y/\gamma}{1 + vu'_x/c^2}\right), \, u_z = \left(\dfrac{u'_z/\gamma}{1 + vu'_x/c^2}\right). \nonumber \]
将此与经典力学的伽利略变换所说的速度变换进行比较,只需添加为向量即可:
\[u_x = u'_x + u, \, u_y = u'_y, \, u_z = u'_z. \nonumber \]
当帧的相对速度远小于光速时,也就是说,当\(v\gg c,\)狭义相对论速度加法定律简化为伽利略速度定律时。 当\(S'\)相对速度\(v\)与光速\(S\)相当时,相对论速度加法定律得出的结果比经典(伽利略)速度加法要小得多。
假设一艘太空飞船以一半的光速直接驶向地球,通过激光产生的光束向我们发送信号(图\(\PageIndex{2}\))。 假设光线以从飞船上观察到的速度\(c\)离开飞船,请计算它接近地球的速度。
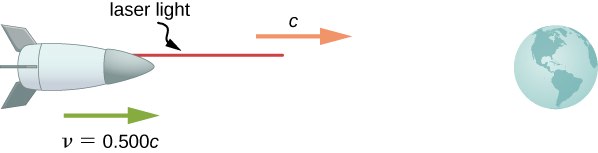
策略
因为光和太空飞船以相对论的速度移动,所以我们不能使用简单的速度加法。 相反,我们使用相对论速度加法来确定光线接近地球的速度。
解决方案
识别已知数:\(v = 0.500c\);\(u' = c\).
识别未知事物:\(u\).
将答案表示为方程式:\(u = \dfrac{v + u'}{1 + \dfrac{vu'}{c^2}}\).
进行计算:
\[ \begin{align*} u &= \dfrac{v + u'}{1 + \dfrac{vu'}{c^2}} \\[4pt] &= \dfrac{0.500c + c}{1 + \dfrac{(0.500c) (c)}{c^2}} \\[4pt] &= \dfrac{(0.500 + 1)c}{\left(\dfrac{c^2 + 0.500c^2}{c^2}\right)} = c. \end{align*} \nonumber \]
意义
相对论速度加法得出正确的结果。 光线迅速离开飞船\(c\)并快速接近地球\(c\)。 光速与光源和观察者的相对运动无关,无论观察者是在船上还是在地球上。
速度加起来不能大于光速,前提\(v\)是光速小于\(c\)且\(u'\)不超过\(c\)。 以下示例说明相对论速度加法不像传统速度加法那样对称。
假设前面示例中的太空飞船以一半的光速接近地球,并以为\(0.750c\)(图\(\PageIndex{3}\))的速度发射罐子。
- 如果罐子直接射向地球,地球观察者能以多快的速度看到它?
- 如果它是在远离地球的地方直接射击的?
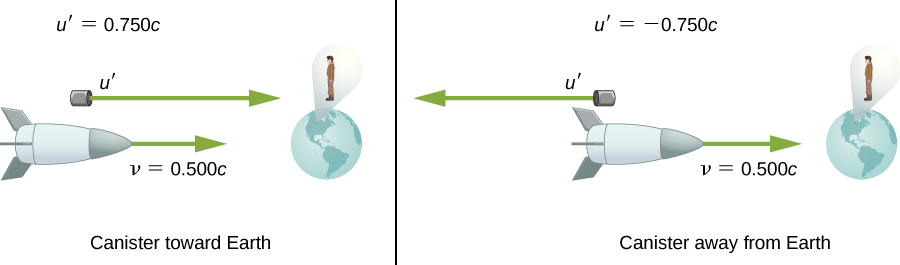
策略
由于罐子和太空飞船以相对论的速度移动,我们必须由地球观察者使用相对论速度加法而不是简单的速度加法来确定罐子的速度。
(a) 的解决方案
- 识别已知数:\(v = 0.500c\);\(u' = 0.750c\).
- 识别未知事物:\(u\).
- 将答案表示为方程式:\(u = \dfrac{v + u'}{1 + \dfrac{vu'}{c^2}}\).
- 进行计算:\[\begin{align*} u &= \dfrac{v + u'}{1 + \dfrac{vu'}{c^2}} \\[4pt] &= \dfrac{0.500c + 0.750c}{1 + \dfrac{(0.500c)(0.750c)}{c^2}} \\[4pt] &= 0.909c. \end{align*} \nonumber \]
(b) 的解决方案
- 识别已知数:\(v = 0.500c\);\(u' = - 0.750c\).
- 识别未知事物:\(u\).
- 将答案表示为方程式:\(u = \dfrac{v + u'}{1 + \dfrac{vu'}{c^2}}\).
- 进行计算:\[\begin{align*} u &= \dfrac{v + u'}{1 + \dfrac{vu'}{c^2}} \\[4pt] &= \dfrac{0.500c + (-0.750c)}{1 + \dfrac{(0.500c)(-0.750c)}{c^2}} \\[4pt] &=- 0.400c. \end{align*} \nonumber \]
意义
减号表示远离地球的速度(与地球的方向相反\(v\)),这意味着罐子如预期的那样在(a)部分朝向地球,在(b)部分向外移动。 但是相对论速度的增加并不像传统上那样简单。 在(a)部分中,罐子确实更快地接近地球,但小于给出的速度的矢量和\(1.250c\)。 在 (b) 部分中,罐子以 −0.400c 的速度离开地球,这比传统上预期的 −0.250c 要快。 速度的差异甚至不是对称的:在部分(a)中,地球上的观察者看到罐子和飞船以0.409 摄氏度的速度分开,(b)以0.900 c 的速度移动。
在两个帧中,沿垂直于两帧相对运动的方向的距离是相同的。 那么,为什么两帧中垂直于 x 方向的速度不同呢?
- 回答
-
尽管在两个参考系中,垂直于相对运动的位移是相同的,但事件之间的时间间隔不同,\(dt\)并且\(dt'\)从两个坐标系中可以看出不同的速度。


