5.6: 洛伦兹转型
- Page ID
- 202135
- 描述经典力学的伽利略变换,将不同惯性系中测得的位置、时间、速度和加速度联系起来
- 导出相应的洛伦兹变换方程,与伽利略变换相比,该方程与狭义相对论一致
- 从四维时空的角度解释洛伦兹变换和相对论的许多特征
我们使用相对论的假设来研究不同参考系中的观察者如何测量不同的长度和时间间隔值。 我们可以通过研究变换方程来进一步了解相对论的假设如何改变牛顿的时空观,这些方程给出一个惯性参考系中事件的空间和时间坐标与另一个惯性参考系中的事件的空间和时间坐标。 我们首先根据牛顿物理学中的视角研究惯性帧之间的位置和时间坐标是如何转换的。 然后我们研究如何改变这种情况才能与相对论的假设一致。 最后,我们研究了由此产生的洛伦兹变换方程及其在四维时空图方面的一些后果,以支持狭义相对论的后果来自时间和空间本身的属性,而不是电磁学的观点。
伽利略变换方程
事件由其\((x, y, z, t)\)相对于一个特定惯性参照系的位置和时间来指定\(S\)。 举个例子,\((x, y, z, t)\)可以表示粒子在某个时间的位置\(t\),我们可以观察许多不同的时间以跟踪粒子的运动。 假设第二个参考系相对于第一个参考\(v\)系的速度\(S'\)移动。 为简单起见,假设这个相对速度是沿 x 轴方向的。 那么,两个参照系中的时间和坐标之间的关系就是
\[\begin{align} x &= x' + vt \label{eq1} \\[4pt] y &= y' \label{eq2} \\[4pt] x &= z'. \label{eq3} \end{align} \]
这些方程中隐含的假设是观察者在\(S\)和\(S'\)中进行的时间测量值相同。 也就是说,
\[t = t' \label{eq4} \]
方程\ ref {eq1}-\ ref {eq4} 统称为伽利略变换。
我们可以通过将伽利略速度和加速度转换方程相对于时间进行微分来获得这些方程。 在本章中,我们将粒子的速度与两个参考系的相对速度区分开来。\(u\)\(v\) 请注意,对于伽利略变换,两帧中用于微分计算粒子速度的时间增量是相同的\(dt = dt'\)。 差异化收益率
\[u_x = u'_x + v, \,u_y = u'_y, \,u_z = u'_z \nonumber \]
和
\[a_x = a'_x, \,a_y = a'_y, \,a_z = a'_z. \nonumber \]
我们用粒子的速度来表示粒子的速度,\(u\)而不是\(v\)为了避免与一个参考\(v\)系相对于另一个参考系的速度混淆。 每帧中的速度因一帧与另一帧的速度而异。 两个参考系中的观察者测量的加速度值相同。 由于变换后质量没有变化,并且点之间的距离没有带电,因此两个帧中的观察者在所有惯性帧中看到物体之间\(F = ma\)作用的力相同,牛顿第二定律和第三定律的形式也相同。 力学定律与相对论的第一个假设是一致的。
洛伦兹变换方程
尽管如此,伽利略变换违反了爱因斯坦的假设,因为速度方程指出,\(c\)沿 x 轴速度移动的光脉冲将在另一个惯性帧\(c - v\)中以速度传播。 具体而言,球形脉冲\(r = ct\)在未底漆帧\(t\)中有时间半径,在底图帧中的半径\(r' = ct'\)在时间 t 处也有半径。 用笛卡尔坐标表示这些关系可以得出
\[ \begin{align} x^2 + y^2 + z^2 - c^2t^2 &= 0 \label{eq21} \\[4pt] x'^2 + y'^2 + z'^2 - c^2t'^2 &= 0. \label{eq22} \end{align} \]
左边的方程\ ref {eq21} 和\ ref {eq22} 可以设置为相等,因为两者都为零。 因为\(y = y'\)而且\(z = z'\),我们获得了
\[x^2 - c^2t^2 = x'^2 - c^2t'^2. \nonumber \]
如果我们假设伽利略变换\(v\)的结果是,那么对于两个帧的非零相对速度,这是无法满足\(t = t'\)的\(x = x' + vt'\)。
要找到正确的变换方程组,请假设两个坐标系\(S\)和\(S'\)图\(\PageIndex{1}\)。 首先假设事件发生\((x', 0, 0, t')\)在 in\(S'\) 和 at\((x, 0, 0, t)\) in\(S\),如图所示\(\PageIndex{1}\)。
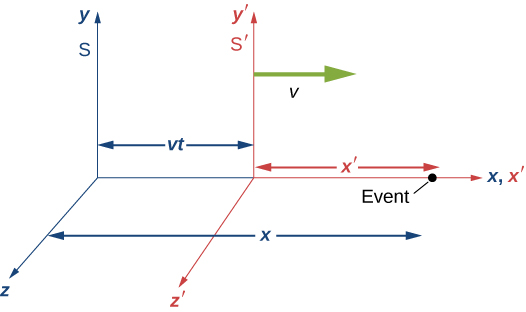
假设在 S 和 S 坐标系的起点重合的那一刻,闪光灯泡会从原点开始发出球形扩散的光脉冲。 在时间 t 处,S 中的观察者发现 S 的起点位于\(x = vt\)。 在 S 中的朋友的帮助下,S 观察者还测量了从事件到 S 起点的距离,并发现它是 S 的起点\(x'\sqrt{1 - v^2/c^2}\)。 之所以如此,是因为我们已经证明相对论的假设意味着长度收缩。 因此,事件在 S 中的位置为
\[x = vt + x'\sqrt{1 - v^2/c^2} \nonumber \]
和
\[x' = \dfrac{x - vt}{x'\sqrt{1 - v^2/c^2}}. \label{eq10} \]
相对论的假设意味着该方程将球面波锋的距离和时间联系起来:
\[x^2 + y^2 + z^2 - c^2t^2 = 0 \nonumber \]
必须同时应用底漆坐标和未底漆坐标,如上所示,方程式为:
\[x^2 - c^2t^2 = x'^2 - c^2t'^2. \nonumber \]
我们将其与关联\(x\)的方程\ ref {eq10} 相结合,\(x′\)得出\(t\)和之间的关系\(t'\):
\[t' = \dfrac{t - vx/c^2}{\sqrt{1 - v^2/c^2}}. \nonumber \]
然后,与事件的时间和位置有关的方程式\(S\)如下所示
\[ \begin{align} t &= \dfrac{t' + vx'/c^2}{\sqrt{1 - v^2/c^2}}. \\[4pt] x &= \dfrac{x' + vt'}{\sqrt{1 - v^2/c^2}}. \\[4pt] y &= y' \\[4pt] z &= z'. \end {align} \nonumber \]
这组方程将两个惯性帧中的位置和时间联系起来,被称为洛伦兹变换。 它们的名字是为了纪念最初提出它们的 H.A. Lorentz(1853—1928 年)。 有趣的是,他以最终被发现为谬误的假设为这种转变辩护。 正确的理论基础是爱因斯坦的狭义相对论。
反向变换用 S\(S\) 中的变量来表示变量。 只需将初始变量和未引数变量互换并进行替换即可得到:
\[\begin{align*} t'& = \dfrac{t - vx/c^2}{\sqrt{1 - v^2/c^2}} \\[4pt] x' &= \dfrac{x - vt}{\sqrt{1 - v^2/c^2}} \\[4pt] y' &= y \\[4pt] z' &= z. \end{align*} \nonumber \]
当航天器 S 以相对速度通过 Alpha Centauri 时,航天器 S 正在驶向 Alpha Centauri c /2。 S的船长根据该船的时钟发送持续1.2秒的无线电信号。 使用洛伦兹变换找到由太空飞船 S 的通信官员测量的信号的时间间隔。
解决方案
- 识别已知的:\(\Delta t' = t'_2 - t'_1 = 1.2 s; \,\Delta x' = x'_2 - x'_1 = 0.\)
- 识别未知事物:\(\Delta t = t_2 - t_1\).
- 将答案表示为方程式。 时间信号从 (\(x', t'_1\)) 开始,在 () 处停止。\(x', t'_1\) 请注意,两个事件的 x' 坐标是相同的,因为时钟在 S 中处于静止状态。 用\(\Delta t = t_2 - t_1\)、\(\Delta x = x_2 - x_1\)和类似的方式写出第一个洛伦兹变换方程,如下所示:
\[\Delta t = \dfrac{\Delta t' + v\Delta x'/c^2}{\sqrt{1 - \dfrac{v^2}{c^2}}}. \nonumber \]
因为时钟在 S 中的位置是固定的\(\Delta x' = 0\),所以时间间隔\(\Delta t\)变为:\[\Delta t = \dfrac{\Delta t'}{\sqrt{1 - \dfrac{v^2}{c^2}}}. \nonumber \]
- 进行计算。
有了\(\Delta t' = 1.2 \,s\)这个:
\[\begin{align*} \Delta t &= \dfrac{1.2 \,s}{\sqrt{1 - \left(\dfrac{1}{2}\right)^2}} \\[4pt] &= 1.6 \,s. \end{align*} \nonumber \]
请注意,洛伦兹变换再现了时间膨胀方程。
测量师在地球坐标系中测量出一条街道的\(L = 100 \,m\)长度\(S\)。 使用洛伦兹变换获得从太空飞船测量的长度的表达式\(S'\)\(0.20c\),假设两帧的\(x\)坐标在时间上重合\(t = 0\)。
解决方案
- 识别已知的:\(L = 100 \,m\);\(v = 0.20 c\);\(\Delta \tau = 0\)。
- 识别未知事物:\(L'\).
- 将答案表示为方程式。 S 帧中的测量师同时测量了棍子的两端,发现它们处于\(x_2\)静止状态且\(L = x_2 - x_1 = 100 \,m\)相距\(x_1\)一段距离。 太空飞船机组人员测量框架中棍棒末端的同时位置。 要将观察者分别在 S 和 S 中记录的长度关联起来,请将四个洛伦兹变换方程中的第二个写成:
\[\begin{align*} x'_2 - x'_1 &= \dfrac{x_2 - vt}{\sqrt{1 - v^2/c^2}} - \dfrac{x_1 - vt}{\sqrt{1 - v^2/c^2}} \\[4pt] &= \dfrac{x_2 - x_2}{\sqrt{1 - v^2/c^2}} \\[4pt] &= \dfrac{L}{\sqrt{1 - v^2/c^2}}. \end{align*} \nonumber \]
- 进行计算。 因为\(x_2 - x_1 = 100 \,m\),移动摇杆的长度等于:
\[\begin{align*} L' &= (100 \,m)\sqrt{1 - v^2/c^2} \\[4pt] &= (100 \,m)\sqrt{1 - (0.20)^2} = 98.0 \,m. \end{align*} \nonumber \]
请注意,洛伦兹变换给出了街道的长度收缩方程。
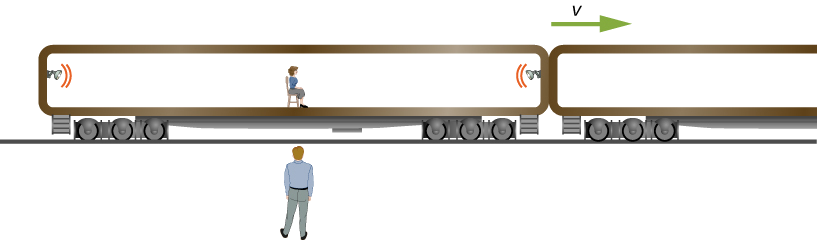
图中所示的观察者\(\PageIndex{2}\)站在铁轨旁看到,当汽车中间以 c /2 的速度经过时,两个灯泡在 26 米长的乘用车的两端同时闪烁。 找出灯泡闪烁的时间间隔,就像坐在车中间的火车乘客所看到的那样。
解决方案
- 识别已知的:\(\Delta t = 0\).
请注意,两个事件的空间分离是在两盏灯之间,而不是灯与乘客的距离。
- 识别未知事物:\(\Delta t' = t'_2 - t'_1.\).
同样,请注意,时间间隔是在灯光闪烁之间,而不是到达乘客的到达时间之间。
- 将答案表示为方程式:
\[\Delta t = \dfrac{\Delta t' + v\Delta x'/c^2}{\sqrt{1 - v^2/c^2}}. \nonumber \]
- 进行计算:
\[\begin{align*} 0 &= \dfrac{\Delta t' + \dfrac{c}{2} (26 \,m)/c^2}{\sqrt{1 - v^2/c^2}} \\[4pt] \Delta t' &= - \dfrac{26 \,m/s}{2c} = - \dfrac{26 \,m/s}{2(3.00 \times 10^8 \,m/s)} \\[4pt] &= -4.33 \times 10^{-8}\,s. \end{align*} \nonumber \]
意义
该符号表示较大的事件,\(x'_2\)即右起的闪光灯,最先出现在 S 帧中,如本例前面所示,因此\(t_2 < t_1\)。
时空
相对论现象可以根据四维时空中的事件进行分析。 当以这种方式看待双胞胎悖论、时间膨胀、长度收缩以及同时性对相对运动的依赖性等现象时,它们被视为时空本质的特征,而不是电磁学的特定方面。
在三维空间中,位置由一组笛卡尔轴上的三个坐标指定,一个点与另一个点的位移由下式给出:
\[(\Delta x, \,\Delta y, \,\Delta z) = (x_2 - x_1, \,y_2 - y-1, \,z_2 - z_1). \nonumber \]
两点\(\Delta r\)之间的距离为
\[\Delta r^2 = (\Delta x)^2 + (\Delta y)^2 + (\Delta z)^2. \nonumber \]
在轴的旋转下,\(\Delta r\)距离是不变的。 如果使用一组新的笛卡尔轴,相对于原始轴围绕原点旋转,则空间中的每个点都将有新的坐标相对于新坐标,但距离由下式\(\Delta r'\)给出
\[\Delta r'^2 = (\Delta x')^2 + (\Delta y')^2 + (\Delta z')^2. \nonumber \]
它的价值与\(\Delta r^2\)以前的值相同。 时空中的洛伦兹变换也会发生类似的情况。
定义两个事件之间的分隔,每个事件由一组 x、y、z 和 ct 在时空中沿四维笛卡尔轴系给出,如下所示
\[(\Delta x, \,\Delta y, \,\Delta z, \,c\Delta t) = (x_2 - x_1, \,y_2 - y_1, \,z_2 - z_1, \,c(t_2 - t_1)). \nonumber \]
还将两个事件\(Δs\)之间的时空间隔定义为
\[\Delta s^2 = (\Delta x)^2 + (\Delta y)^2 + (\Delta z)^2 - (c\Delta t)^2. \nonumber \]
如果两个事件在所考虑的参考系中具有相同的 ct 值,则\(\Delta s\)将对应于空间中点\(\Delta r\)之间的距离。
粒子穿越时空的路径由指定其每次运动位置的事件(x、y、zct)组成。 穿越时空的路径被称为粒子的世界线。 静止在同一位置的粒子的世界线是一条平行于时间轴的直线。 如果粒子以平行于 x 轴的恒定速度移动,则其世界线将是一条倾斜的线\(x = vt\),对应于简单的位移与时间关系图。 如果粒子加速,则其世界线是弯曲的。 s 沿粒子世界线的增量以微分形式给出
\[ds^2 = (dx)^2 + (dy)^2 + (dz)^2 - c^2(dt)^2. \nonumber \]
正如空间轴旋转时\(\Delta r\)距离不变一样,时空间隔:
\[\Delta s^2 = (\Delta x)^2 + (\Delta y)^2 + (\Delta z)^2 - (c\Delta t)^2. \nonumber \]
在洛伦兹变换下是不变的。 这源于相对论的假设,也可以通过将先前的洛伦兹变换方程替换为时空间隔的表达式来看出:
\[\begin{align*} \Delta s^2 = (\Delta x)^2 + (\Delta y)^2 + (\Delta z)^2 - (c\Delta t)^2. \\[4pt] &=\left(\dfrac{\Delta x' + v\Delta t'}{\sqrt{1 - v^2/c^2}}\right)^2 + (\Delta y')^2 + (\Delta z')^2 - \left(c\dfrac{\Delta t' + \dfrac{v\Delta x'}{c^2}}{\sqrt{1 - v^2/c^2}}\right)^2 \nonumber \]\[= (\Delta x')^2 + (\Delta y')^2 + (\Delta z')^2 - (c\Delta t')^2 \\[4pt] &= \Delta s'^2. \end{align*} \nonumber \]
此外,洛伦兹变换改变时空中事件的坐标与三维旋转将旧坐标转换为新坐标的方式类似:
|
洛伦兹变换(x, t 坐标): |
AXIS—围绕 z 旋转-a 轴(x, t 坐标): |
|---|---|
|
\(x' = (γ)x + (−βγ)ct\) |
\(x' = (\cos θ)x + (\sin θ)y\) |
| \(ct' = (−βγ)x + (γ)ct\) | \(y' = (−\sin θ)x + (\cos θ)y\) |
哪里\(\gamma = \dfrac{1}{\sqrt{1 - \beta^2}}\);\(\beta = v/c\)。
洛伦兹变换可以看作是空间旋转到时空的概括。 但是,三维轴旋转和涉及时间轴的洛伦兹变换之间存在一些差异,这是因为度量或测量位移\(\Delta r\)的规则存在差异。\(\Delta s\) 尽管在空间旋转下\(\Delta r\)是不变\(\Delta s\)的,在洛伦兹变换下也是不变的,但涉及时间轴的洛伦兹变换并不能保留某些特征,例如轴保持垂直或沿每个轴的长度刻度保持不变。
请注意,数量\(\Delta s^2\)可以有任一符号,具体取决于所涉及的时空事件的坐标。 对于给出负号的成对事件,定义\(c^2 \Delta \tau^2\)为很有用\(-\Delta s^2\)。 \(c^2 \Delta \tau\)如上所述,其意义如下:在两个事件发生在同一地点的参考框架中,我们有\(\Delta x = \Delta y = \Delta z = 0\),因此(来自方程式\(\Delta s^2 = - c^2 \Delta \tau^2\)):
\[c^2 \Delta \tau^2 = - \Delta s^2 = (c^2 \Delta t)^2. \nonumber \]
因此,\(c^2 \Delta \tau\)是参照系\(c^2 \Delta t\)中两个事件发生在同一地点的时间间隔。 这与前面讨论的适当时间间隔相同。 这也源于\(\Delta s\)和之间的关系\(c^2 \Delta \tau\),因为洛伦兹是不变\(\Delta s\)的,所以正确的时间也是洛伦兹不变量。 所有惯性帧中的所有观察者都同意两个相同事件之间的适当时间间隔。
表明,如果观察者看到粒子随速度移动,则时间增量\(dt\)过去了\(v\),则对应于粒子的正确时间粒子增量\(d\tau = \gamma dt\)。
- 回答
-
从定义正确的时间增量开始:
\[d\tau = \sqrt{-(ds)^2 /c^2} = \sqrt{dt^2 - (dx^2 + dx^2 + dx^2)/c^2}. \nonumber \]
哪里\((dx, dy, dx, cdt)\)是在观察者的惯性框架中测量的,该观察者不一定能看见静止的粒子。 因此,这变成了
\[d\tau = \sqrt{-(ds)^2/c^2} = \sqrt{dt^2 - [(dx)^2 + (dy)^2 + (dz)^2]/c^2} \nonumber \]
\[dt\sqrt{1 - \left[ \left(\dfrac{dx}{dt}\right)^2 + \left(\dfrac{dy}{dt}\right)^2 + \left(\dfrac{dz}{dt}\right)^2\right] /c^2} \nonumber \]\[dt\sqrt{1 - v^2/c^2} \nonumber \]\[dt = \gamma d\tau. \nonumber \]
光锥
我们可以通过想象三个空间坐标由水平轴共同表示,垂直轴作为 ct 轴,来应对四维可视化和绘制图表的困难。 以时空中的特定事件作为所示时空图的原点开始,在事件的初始位置保持静止状态的粒子的世界线即为时间轴。 穿过平行于空间轴的时间轴的任何平面都包含所有相互同步的事件,以及与平面和时间轴交点的所有事件,如事件的剩余帧在原点所示。
在图表上描绘一个由穿过起始事件 A 的所有光束的世界线形成的光锥很有用,如图所示\(\PageIndex{3}\)。 根据相对论的假设,如果时间轴以 ct 为单位测量,则光锥的边角为 45°,而且,根据相对论的假设,所有惯性帧中的光锥都保持不变。 因为事件 A 是任意的,所以时空图中的每个点都有一个与之关联的光锥。
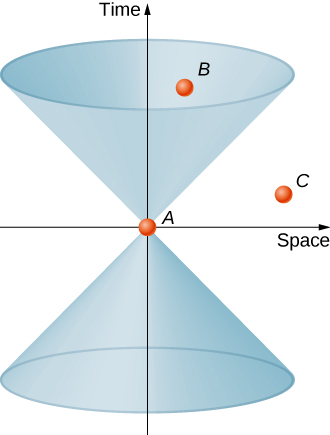
现在考虑一下粒子穿越时空的世界线。 锥体之外的任何世界线,例如从 A 穿过 C 的世界线,都将涉及大于 c 的速度,因此是不可能的。 诸如 C 之类的事件据说位于光锥之外的事件与事件 A 有类似空格的分离。 它们的特点是:
\[\Delta s_{AC}^2 = (x_A - x_C)^2 + (y_A - y_C)^2 + (z_A - z_C)^2 - (c\Delta t)^2 > 0. \nonumber \]
像 B 这样位于上锥体的事件可以在不超过真空中光速的情况下到达,其特点是
\[\Delta s_{AB}^2 = (x_A - x_B)^2 + (y_A - y_B)^2 + (z_A - z_B)^2 - (c\Delta t)^2 <0. \nonumber \]
据说该事件与 A 有着类似时间的分离。 落入光锥上半部分的类时间事件发生在顶点处的 t 值大于事件 A 的时间,并且将来会相对于 A 发生。 与 A 有时间相似的分离并落入光锥下半部分的事件已经过去,可能会影响起点处的事件。 光锥之外的区域被标记为既不是过去也不是未来,而是被标记为 “其他地方”。
对于任何与原点事件有类似空格分离的事件,可以选择一个时间轴来使这两个事件同时发生,这样这两个事件在某个参考系中是同时发生的。 因此,哪些具有类似空间分离的事件在时间上先于另一个事件也取决于观察者的参考框架。 由于只有通过超过光速才能穿越类似空间的分离;这种违反哪个事件可能导致另一个事件的行为为粒子的传播速度不能超过光速提供了另一个论据,也是关于时空旅行的科幻小说的潜在材料。 同样,对于任何与起点事件有时间相似分离的事件,都可以找到一个参考框架,使事件发生在同一地点。 因为关系
\[\Delta s_{AC}^2 = (x_A - x_C)^2 + (y_A - x_C)^2 + (z_A - z_C)^2 - (c\Delta t)^2 > 0. \nonumber \]
和
\[\Delta s_{AB}^2 = (x_A - x_B)^2 + (y_A - y_B)^2 + (z_A - z_B)^2 - (c\Delta t)^2 <0. \nonumber \]
是洛伦兹不变的,无论两个事件是类似时间的,可以使它们发生在同一个地方,还是像空间一样并且可以同时发生,对所有观察者来说都是一样的。 不同惯性参照系中的所有观察者都同意两个事件是具有类时分还是类似空间的分离。
在时空中看到的双胞胎悖论
前面讨论的双胞胎悖论涉及一对宇航员双胞胎以接近光速行驶到遥远的恒星系统,然后返回地球。 由于时间扩张,预计太空双胞胎的年龄将远低于地球双胞胎。 这似乎是自相矛盾的,因为乍一看我们可能预料到相对运动是对称的,但天真地认为也可以争辩说地球上的双胞胎应该减少衰老。
要用时空图对此进行分析,请假设所用轴的原点在地球上是固定的。 然后,地球双胞胎的世界线沿着时间轴行驶。
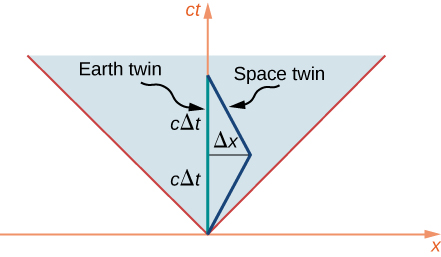
宇航员双胞胎前往遥远的恒星然后返回,其世界线必须偏离直线路径才能允许回程。 如图所示\(\PageIndex{4}\),两对双胞胎的情况根本不对称。 它们在时空中的路径长度明显不同。 具体来说,Earthbound Twin 的世界线有长度\(2c\Delta t\),这就给出了地球双胞胎经过的适当时间\(2\Delta t\)。 到遥远的恒星系统的距离是\(\Delta x = v\Delta t\)。 太空双胞胎的正确时间\(2\Delta \tau\)在哪里
\[c^2\Delta \tau^2 = - \Delta s^2 = (c\Delta t)^2 - (\Delta x)^2. \nonumber \]
按比例计算,这比地球双胞胎的正确时间要短得多
\[\dfrac{c\Delta \tau}{c\Delta t} = \sqrt{\dfrac{(c\Delta t)^2 - (\Delta x)^2}{(c\Delta t)^2}} = \sqrt{\dfrac{(c\Delta t)^2 - (v\Delta t)^2}{(c\Delta t)^2}} = \sqrt{1 - \dfrac{v^2}{c^2}} = \dfrac{1}{\gamma}. \nonumber \]
与时间膨胀公式一致。 因此,双胞胎悖论被认为根本不是悖论。 在时空图中,两个双胞胎的情况并不对称。 唯一令人惊讶的是,时空图上看似较长的路径对应于较小的正确时间间隔,这是因为\(\Delta \tau\)和\(\Delta s\)依赖于\(\Delta x\)和\(\Delta t\)。
时空中的洛伦兹变换
我们已经注意到洛伦兹转型是如何离开的
\[\Delta s^2 = (\Delta x)^2 + (\Delta y)^2 + (\Delta z)^2 - (c\Delta t)^2. \nonumber \]
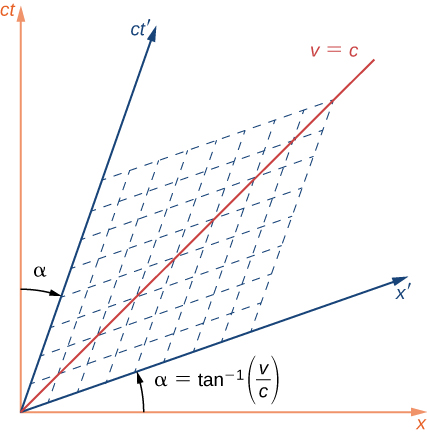
不变,对应于四维时空中轴的旋转。 如果 S 和 S 帧沿着其共享的 x 方向相对运动,则 S 的空间和时间轴将旋转一个角度 αα,如 S 所示\(\PageIndex{5}\),其中:
\[tan \,\alpha = \dfrac{v}{c} = \beta. \nonumber \]
这与通常的三维意义上的旋转不同,因为两个时空轴以剪刀般的方式对称地相互旋转,如图所示。 时间轴和空间轴的旋转角度相同。 平行于两个轴的虚线网格显示了如何沿着原始轴读取事件的坐标。 这可以通过沿一条平行于 x' 的直线和一条平行于 t 轴的直线来完成,如虚线所示。 两个轴的长度标度通过以下方式更改:
\[ct' = ct\sqrt{\dfrac{1 + \beta^2}{1 - \beta^2}}; \,x' = x\sqrt{\dfrac{1 + \beta^2}{1 - \beta^2}}. \nonumber \]
根据相对论的第二个假设,在 x 轴 45° 处标有 “v = c” 的直线对应于光锥的边缘,不受洛伦兹变换的影响。 在 S 和 S 参考系中,“v = c” 线及其所代表的光锥是相同的。
同时性
不同地点发生事件的同时性取决于用来描述它们的参考框架,如上所述,用剪刀般的 “旋转” 到新的时空坐标即可。 如果两个事件在未引用的参考系中具有相同的\(t\)值,则它们不必沿着\(ct'\)-轴测量具有相同的值,因此在初始帧中也不会同时发生。
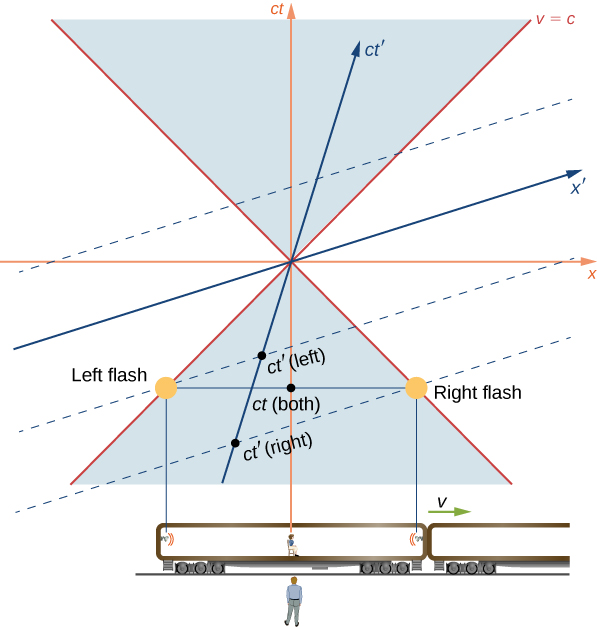
举一个具体的例子,以近光速列车为例,其中汽车两端的闪光灯在地面观察者的参考框架中同时闪烁。 时空图如图所示\(\PageIndex{6}\)。 两盏灯的闪光由过去位于光锥上标有 “左闪光灯” 和 “右闪光灯” 的点表示。 两个脉冲的世界线沿着光锥的边缘移动,同时到达地面上的观察者。 他们的到来是事件的起源。 因此,它们必须在未涂底漆的帧中同时发射,由标记为\(t\)(两者)的点表示。 但是时间是在坐在火车车厢中间的观察者的参考框架中沿 ct'-axis 测量的。 因此,在她的参考框架中,标有\(t'\)(左)和\(t'\)(右)的灯泡的发射事件不是同时发生的。
就时空图而言,两个观察者只是对相同的事件使用不同的时间轴,因为它们处于不同的惯性框架中,而且两个观察者的结论同样有效。 正如对时空图的分析进一步表明的那样,事件的同时性如何取决于参考框架的特性来自空间和时间本身的特性,而不是任何专门与电磁学有关的特性。


