5.5: 长度收缩
- Page ID
- 202084
在本节结束时,您将能够:
- 解释同时性与长度收缩之间的关系。
- 描述长度收缩和时间膨胀之间的关系,并用它来推导长度收缩方程。
图\(\PageIndex{1}\)中所有乘客的火车车厢长度相同。 他们都将就汽车两端的同时位置达成一致,并就它们之间的距离获得相同的结果。 但是,一个惯性帧中的同步事件不必在另一个惯性帧中同时发生。 如果火车能够以相对论的速度行驶,那么地面上的观察者将看到汽车两个端点的同步位置,其距离与车内的观察者相距不同。 当涉及相对论速度时,不同观察者的测得距离不必相同。

合适的长度
两个观察者彼此经过总是看到他们相对速度的相同值。 尽管时间膨胀意味着火车乘客和站在轨道旁的观察者测量列车通过的时间不同,但他们仍然同意相对速度,即距离除以经过的时间,是相同的。 如果地面上的观察者和火车上的观察者测量的列车通过地面观察者的长度的时间不同,那么就他们的相对速度达成共识意味着他们还必须看到不同的行驶距离。
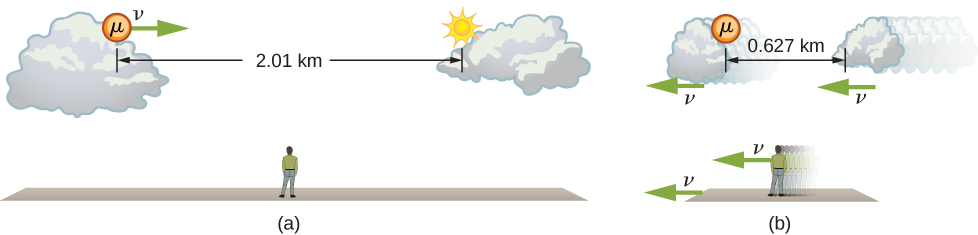
前面讨论的 muon 说明了这个概念(图\(\PageIndex{2}\))。 对于地球上的观察者来说,μ子从产生到衰变,在0.950 摄氏度的温度下传播7.05微秒。 因此,它相对于地球的行进距离为:
\[ \begin{align*} L_0 &= v\Delta t \\[4pt] &= (0.950)(3.00 \times 10^8 \, m/s)(7.05 \times 10^{-6}s) \\[4pt] &= 2.01 \, km. \end{align*} \nonumber \]
在μ子框架中,μ子的寿命为2.20 μs。 在这个参照框架中,地球、空中和地面只有足够的时间旅行:
\[ \begin{align*} L &= v\Delta r \\[4pt] &= (0.950)(3.00 \times 10^8 \, m/s)(2.20 \times 10^{-6}s) \\[4pt] &= 0.627 \, km. \end{align*} \nonumber \]
相同的两个事件(μ子的产生和衰变)之间的距离取决于谁测量它以及它们相对于它的移动方式。
正确长度\(L_0\)是两点之间的距离,由处于静止状态的观察者相对于两点测得的距离。
地球观测器测量的长度是正确的,\(L_0\)因为μ子的产生点和衰变点相对于地球是静止的。 对介子来说,地球、空气和云层都在移动,所以它看到的距离 L 的长度不合适。
长度收缩
要关联不同观察者测量的距离,请注意,在我们的μ子示例中,相对于地球观测器的速度由下式给出
\[v = \dfrac{L_0}{\Delta t}. \nonumber \]
相对于地球观测者的时间是\(Δt\),因为被计时的物体正在相对于这个观察者移动。 相对于移动观察点的速度由下式给出
\[v = \dfrac{L}{\Delta \tau}. \nonumber \]
移动的观察者随着 muon 一起移动,因此观察到正确的时间\(\Delta \tau\)。 两种速度是相同的;因此,
\[\dfrac{L_0}{\Delta t} = \dfrac{L}{\Delta \tau}. \label{eq10} \]
我们知道这一点\(\Delta t = \gamma \Delta \tau\),用它代入方程\ ref {eq10} 可以得出
\[L = \dfrac{L_0}{\gamma}. \nonumber \]
用替换\(γ\)可以得出一个与不同观察者测量的距离相关的方程。
长度收缩是指在相对于物体移动的参考系中测量时,物体的测量长度从其适当长度减小:
\[L = L_0\sqrt{1 - \dfrac{v^2}{c^2}} \label{contraction} \]
其中\(L_0\)是物体在其静止帧中的长度,\(L\)是帧中随速度移动的长度\(v\)。
如果我们测量任何相对于框架移动的长度,我们会发现它的长度 L 小于物体静止时所测量的正确长度\(L_0\)。 例如,在μ子的静止坐标系中,地球在μ子的产生位置和其衰变位置之间移动的距离小于从地球框架上看到的行进距离。 这些点相对于地球是固定的,但相对于μ子移动。 从 muon 的静止帧中可以看出,云和其他物体也会沿着运动方向收缩。
因此,两个观察者沿其相对运动方向测量不同的距离,这取决于哪一个观察者在测量静止物体之间的距离。
但是在垂直于相对运动的方向上测量的距离呢? 想象一下,两个观察者沿着他们的 x 轴移动并互相通过,同时在 y 方向上垂直握住仪表杆。 该图\(\PageIndex{3}\)显示了在两个男孩 S 和 S 的参考系中分别处于静止状态的两根仪表 M 和 M'。 一把小画笔贴在棍子 M' 的顶部(100 厘米的标记)上。 假设 S 相对于 S 以非常高的速度 v 向右移动,并且摇杆的方向使其垂直或横向于其相对速度向量。 握住棍棒时,它们的下端(0 厘米标记)重合。 假设 S 之后看着他的棍子 M 时,他发现上面画了一条线,就在棍子的顶部下方。 因为刷子附着在另一个男孩的棍子 M' 的顶部,所以 S 只能得出结论,棍子 M' 的长度小于 1.0 m。
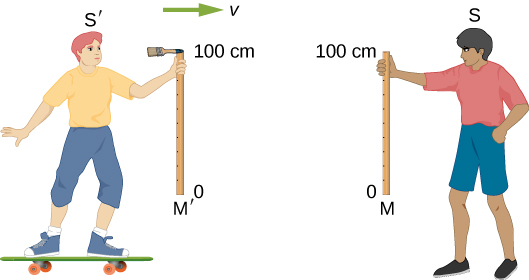
现在,当男孩们互相接近时,S,就像 S 一样,看见一根仪表棒以速度 v 向他移动。 因为他们的处境是对称的,所以每个男孩都必须对另一帧中的棍子进行相同的测量。 因此,如果 S 测量的棒 M' 长度小于 1.0 m,则 S 的长度必须小于 1.0 m,而 S 必须看到他的画笔越过棍子 M 的顶部,而不是在上面画一条线。 换句话说,在同一个事件之后,一个男孩看见棍子上画了一条线,而另一个男孩在同一根棍子上看不到这样的线!
爱因斯坦的第一个假设要求物理定律(例如,应用于绘画)预测处于惯性帧中的 S 和 S 会进行相同的观测;也就是说,S 和 S 必须要么都看见在摇杆 M 上画的线,要么两者都看不见那条线。 因此,我们不得不得出我们最初的假设,即 S 看见 S 在棍子顶部下方画了一条线是错误的! 相反,S 找到了在 M 上 100 厘米处绘制的直线。然后两个男孩都会同意在 M 上画一条线,他们也会同意两根棍子的长度恰好是 1 m。 然后我们得出结论,在不同的惯性坐标系中,横向长度的测量值必须相同。
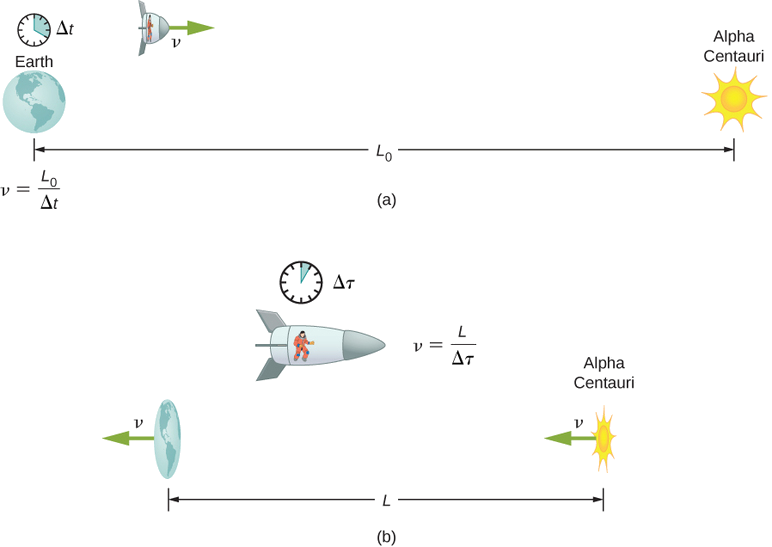
假设宇航员,比如双胞胎悖论讨论中的双胞胎,行进速度如此之快\(\gamma = 30.00\)。 (a) 宇航员从地球前往最近的恒星系统,即半人马座阿尔法,距离地球观测者测量,距离4.300光年。 根据宇航员的测量,地球和半人马座阿尔法相距多远? (b) 就 c 而言,宇航员相对于地球的速度是多少? 你可能会忽略地球相对于太阳的运动(图\(\PageIndex{4}\))。
策略
首先,请注意,在天文尺度上,光年(ly)是一种方便的距离单位,它是光在一年内传播的距离。 对于 (a) 部分,半人马座阿尔法和地球之间的距离是正确的距离\(L_0\),因为它是由两颗恒星(大约)静止的地球观察者测量的。 对宇航员来说,Earth 和 Alpha Centauri 以相同的速度移过,因此它们之间的距离是收缩长度 L。 在 (b) 部分中,我们被给出了\(\gamma\),所以我们可以\(v\)通过重新排列 to express\(v\) 的定义\(\gamma\)来找到\(c\)。
(a) 的解决方案
对于 (a) 部分:
- 找出已知数:\(L_0 = 4.300 \, ly\);\(\gamma = 30.00.\)
- 识别未知事物:L.
- 将答案表示为方程式:\(L = \dfrac{L_0}{\gamma}\).
- 进行计算:
\[\begin{align*} L &= \dfrac{L_0}{\gamma} \\[4pt] &= \dfrac{4.300 \, ly}{30.00} \\[4pt] &= 0.1433 \, ly. \end{align*} \nonumber \]
(b) 的解决方案
对于 (b) 部分:
- 识别已知的:\(\gamma = 30.00\).
- 识别未知数:用 c 表示的 v。
- 将答案表示为方程式。 从以下开始:
\[\gamma = \dfrac{1}{\sqrt{1 - \dfrac{v^2}{c^2}}}. \nonumber \]
然后求解未知的 v/c,首先对两边进行平方,然后重新排列:\[\begin{align*} \gamma^2 &= \dfrac{1}{1 - \dfrac{v^2}{c^2}} \\[4pt] \dfrac{v^2}{c^2} &= 1 - \dfrac{1}{\gamma^2} \\[4pt] \dfrac{v}{c} &= \sqrt{1 - \dfrac{1}{\gamma^2}}. \end{align*} \nonumber \]
- 进行计算:
\[\begin{align*} \dfrac{v}{c} &= \sqrt{1 - \dfrac{1}{\gamma^2}} \\[4pt] &= \sqrt{1 - \dfrac{1}{(30.00)^2}} \\[4pt] &= 0.99944\end{align*} \nonumber \]
或者\[v = 0.9994 \, c. \nonumber \]
意义:切记在得到最终答案之前不要对计算结果进行四舍五入,否则你可能会得到错误的结果。 在狭义相对论计算中尤其如此,只有在小数点后才会显示差异。 这里的相对论效应很大 (\(\gamma = 30.00\)),我们看到 v 正在接近(不等于)光速。 因为宇航员测量的距离要小得多,所以宇航员可以在更短的时间内在她的画面中行驶。
以极高的速度旅行的人可以行驶很远的距离(数千甚至数百万光年),并且在途中只能老化几年。 但是,就像过去几个世纪离开家园的移民一样,这些人将永远离开他们所熟悉的地球。 即使他们回来了,地球上也将经过数千到数百万年,摧毁现在存在的大部分东西。 以这样的速度行驶还有更严重的实际障碍;要达到如此高的速度,所需的能量远远超过传统物理学预测所能获得的能量。 本章稍后将对此进行讨论。
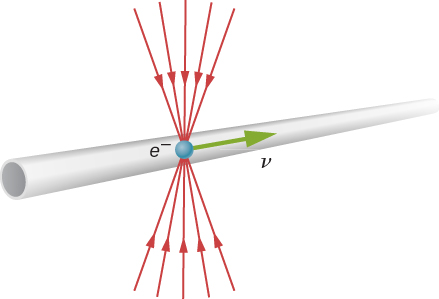
为什么我们没有注意到日常生活中的长度收缩? 到杂货店的距离似乎并不取决于我们是否要搬家。 通过研究方程\ ref {contraction},我们可以看到,在低速 (\(v \ll c\)) 下,长度几乎相等,这是经典的预期。 但是,长度收缩是真实的,如果不是常见的话。 例如,如静止观察者所见,带电粒子(例如以相对论速度行进的电子)具有沿运动方向压缩的电场线(图\(\PageIndex{5}\))。 当电子通过探测器(例如线圈)时,其磁场的相互作用要短得多,这是在粒子加速器(例如3公里长的斯坦福直线加速器(SLAC)上观察到的效应。 实际上,对于沿着SLAC的光束管道行进的电子来说,加速器和地球都在移动,长度收缩。 相对论效应如此之大,以至于加速器距离电子只有0.5米长。 实际上,将电子束放下管道比较容易,因为电子束不必像落下 3 公里长的管道那样精确地瞄准一条短管道。 这又是对狭义相对论的实验验证。
粒子正在以为的速度穿越地球大气层\(0.750c\)。 对于地球观测者来说,它的行进距离为 2.50 km。 从粒子的参考系来看,粒子会传播多远?
- 回答
-
\[L = L_0\sqrt{1 - \dfrac{v^2}{c^2}} = (2.50 \, km)\sqrt{1 - \dfrac{(0.750c)^2}{c^2}} = 1.65 \, km \nonumber \]


