5.4: 时间扩张
- Page ID
- 202053
在本节结束时,您将能够:
- 解释如何在不同的参考系中以不同的方式测量时间间隔。
- 描述如何区分正确的时间间隔和扩大的时间间隔。
- 描述μ子实验的意义。
- 解释为什么双胞胎悖论不是矛盾。
- 根据给定帧中物体的速度计算时间膨胀。
对同时性的分析表明,爱因斯坦的假设暗示着一个重要的影响:在不同的惯性帧中测量时时间间隔具有不同的值。 例如,假设宇航员测量光脉冲与其飞船运动方向垂直移动一段距离(相对于地面观察者)、从镜子反弹然后返回所花费的时间(图\(\PageIndex{1a}\))。 宇航员在航天器中测量的时间与地球观测者通过观察航天器中发生的事情测量的经过的时间相比如何?
研究这个问题会产生深远的结果。 一个过程所经过的时间取决于哪个观察者正在测量它。 在这种情况下,宇航员(在宇航员静止的太空飞船内)测量的时间小于地球观察者(宇航员正在向其移动)测量的时间。 对于观察者来说,相同过程所花费的时间是不同的,因为光脉冲在宇航员框架中传播的距离小于在地球框架中的传播距离,如图所示\(\PageIndex{1b}\)。 光在每帧中以相同的速度传播,因此在接地帧中传播更远的距离需要更多的时间。
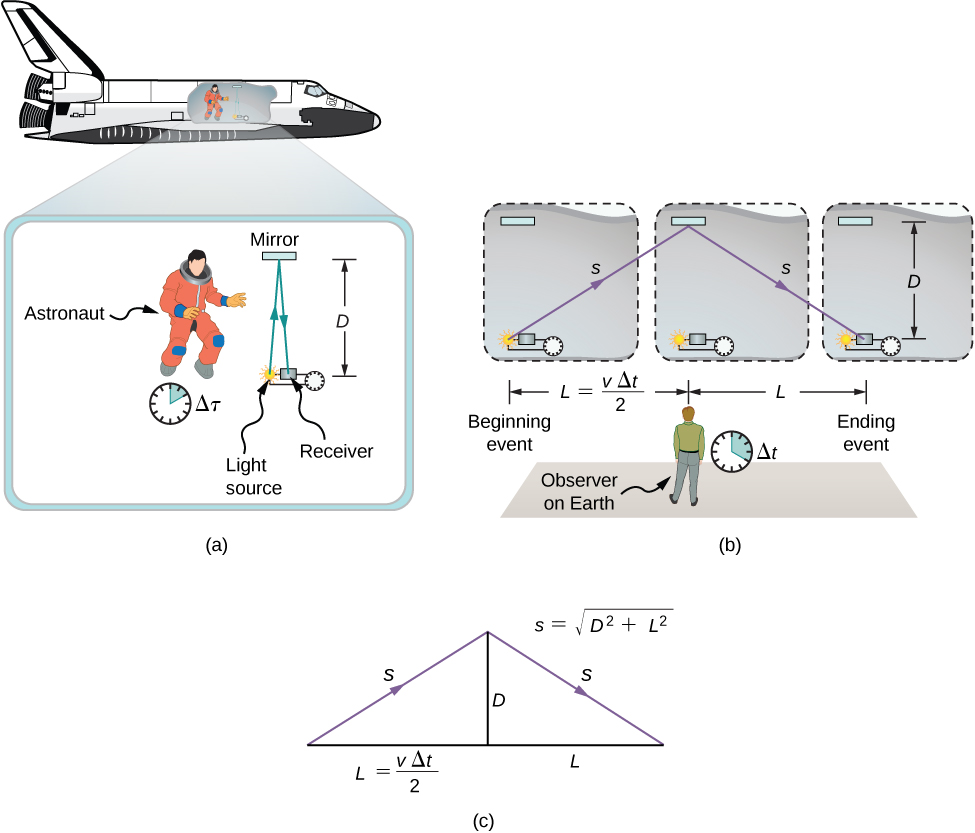
时间膨胀是延长观察者在相对于事件的其余帧(事件发生在同一位置)移动的惯性帧中两个事件之间的时间间隔。
为了定量比较两个惯性帧中的时间测量值,我们可以将图\(\PageIndex{1b}\)中的距离相互关联起来,然后用相应参考系中脉冲的行程时间(分别为\(\Delta t\)或\(\Delta \tau\))来表示每个距离。 然后可以用以下方式求\(\Delta t\)解所得方程\(\Delta \tau\)。
图\(L\)中的长\(D\)度和\(\PageIndex{1c}\)是带有斜边的直角三角形的边缘\(s\)。 从毕达哥拉斯定理来看
\[s^2 = D^2 + L^2. \nonumber \]
长\(2s\)度和分别\(2L\)是光脉冲和航天器在地球观测者框架\(\Delta t\)中及时传播的距离。 长度\(D\)是光脉冲在宇航员帧中随时间\(\Delta \tau\)传播的距离。 这给了我们三个方程式:
\[\begin{align*} 2s &= c\Delta t \\[4pt] 2L &= v\Delta t; \\[4pt] 2D &= c\Delta \tau. \end{align*} \nonumber \]
请注意,我们使用爱因斯坦的第二个假设,将两个惯性帧中的光速均为 c。 我们将这些结果替换为毕达哥拉斯定理的前一个表达式:
\[ \begin{align*} s^2 &= D^2 + L^2 \\[4pt] \left(c\dfrac{\Delta t}{2}\right)^2 &= \left(c\dfrac{\Delta \tau}{2}\right)^2 + \left(v\dfrac{\Delta t}{2}\right)^2 \end{align*} \nonumber \]
然后我们重新排列获取
\[(c\Delta t)^2 - (v\Delta t)^2 = (c\Delta \tau)^2. \nonumber \]
最后,以 of\(\Delta t\) 的角度求解 for\(\Delta \tau\) 会给我们
\[\Delta t = \dfrac{\Delta \tau}{\sqrt{1 - (v/c)^2}}. \nonumber \]
这等同于
\[\Delta t = \gamma \Delta \tau, \label{timedilation} \]
哪里\(\gamma\)是给出的相对论因子(通常称为洛伦兹因子)
\[\gamma = \dfrac{1}{\sqrt{1 - \dfrac{v^2}{c^2}}} \nonumber \]
\(v\)和分别\(c\)是移动的观察者和光的速度。
注意两次测量之间的不对称性。 其中只有一个是测量两个事件(光脉冲的发射和到达)在同一位置之间的时间间隔。 它是对单个时钟剩余帧中的时间间隔的测量。 地球范围内的测量涉及比较在不同地点发生的两个事件之间的时间间隔。 在单个地点发生的事件之间的时间间隔有单独的名称,以将其与地球观察者测量的时间间隔区分开来,我们在本章中使用单独的符号\(\Delta \tau\)来指代它。
两个事件\(\Delta \tau\)之间的正确时间间隔是两个事件发生在同一地点的观察者测量的时间间隔。
这个方程式\(\Delta \tau\)很\(\delta t\)重要,确实很了不起。 首先,如前所述,不同的观察者相对于彼此移动所经过的时间并不相同,尽管两者都处于惯性帧中。 \(\Delta \tau\)对于像宇航员一样随设备移动的观察者来说,适当的时间间隔小于其他观察者的时间间隔。 这是两个事件之间测量的最短时间。 地球观察者认为,相对于观察者相对于地球移动在移动系统中的看法,移动系统内的时间间隔有所扩大(即延长)。 或者,根据地球观察者的说法,移动帧内事件之间的时间间隔更短。 请注意,事件之间经过的最短时间是在惯性帧中,观察者看到事件(例如,光信号的发射和到达)发生在同一点。
这种时间效应是真实的,不是由时钟不准确或测量不当造成的。 对于处于相对运动状态的观察者,同一事件的时间间隔测量值有所不同。 时间的膨胀是时间本身的固有特性。 观察到所有相对于观察者移动的时钟,包括生物钟,例如人的心跳或衰老,与相对于观察者静止的时钟相比,运行速度更慢。
请注意,如果相对速度远小于光速 (v << c),\(v^2/c^2\)则非常小,经过的时间\(\Delta t\)和几乎\(\Delta \tau\)相等。 在低速下,基于现代相对论的物理学接近经典物理学,日常体验涉及非常小的相对论效应。 但是,对于接近光速的速度,\(v^2/c^2\)则接近 1,因此\(\sqrt{1 - v^2/c^2}\)非常小,并且\(\Delta t\)明显大于\(\Delta \tau\)。
介子的半衰期
有大量实验证据表明该方程\(\Delta t = \gamma \Delta \tau\)是正确的。 一个例子是宇宙射线粒子从深空持续降落在地球上。 这些粒子与高层大气中原子核的某些碰撞会产生称为 μ子的寿命短的粒子。 与测量半衰期的观察者相比,介子处于静止状态时的半衰期(一半物质衰变的时间)为1.52微秒。 这是正确的时间间隔\(\Delta \tau\)。 如果牛顿关于时间和空间的假设是正确的,那么这么短的时间允许很少的μ子到达地球表面,也能被探测出来。 但是,宇宙射线粒子产生的μ子有一定速度范围,其中一些在光速附近移动。 已经发现,由地球观测者 (\(\Delta t\)) 测得的μ子的半衰期随速度的变化而变化,这与方程所预测的完全相同\(\Delta t = \gamma \Delta \tau\)。 μ子移动得越快,寿命越长。 我们在地球上看到μ子的持续时间比其在自己的休息框架内预测的半衰期要长得多。 从我们的框架来看,相对于我们,μ子的衰变速度比静止时慢。 结果,更大比例的μ子到达地面。
在我们举出第一个求解相对论问题的例子之前,我们先陈述了一个策略,你可以用它作为这些计算的指导方针。
- 如上所述,列出给出或可以从问题中推断出的内容(找出已知数)。 请特别查看有关相对速度 v 的信息。
- 准确确定问题中需要确定的内容(找出未知数)。
- 在进行任何计算之前,请务必了解问题的概念方面(将答案表示为方程式)。 例如,在使用方程或使用方程进行计算之前,确定哪个观察者看到时间被扩张或长度缩小。 如果你考虑过谁看见了什么,谁在观察事件时移动,谁看到了正确的时间等等,你会发现确定你的计算是否合理要容易得多。
- 确定要进行的主要计算类型以找到上述未知数(进行计算)。 你会发现本节摘要有助于确定是否涉及长度收缩、相对论动能或其他概念。
请注意,在计算过程中不应四舍五入。 如文中所述,您必须经常对多位数进行计算,才能看到预期的效果。 你可以在问题解的最后四舍五入,但在随后的计算中不要使用四舍五入的数字。 另外,请检查答案以查看是否合理:有意义吗? 对于相对论来说,这可能更加困难,因为相对论每天都有很少的例子可以提供合理的经验。 但是你可以寻找大于 c 的速度或方向错误的相对论效应(例如预计会出现扩张的时间收缩)。
Hypersonic Technology Veicle 2(HTV-2)是一种实验性火箭飞行器,能够以 21,000 km/h(5830 m/s)的速度行驶。 如果 HTV-2 中的电子钟测量的时间间隔恰好为 1 秒,那么地球上的观测者将测量的时间间隔是多少?
策略
应用时间膨胀公式,将 HTV-2 中信号的正确时间间隔与在地面上测量的时间间隔关联起来。
解决方案
- 找出已知数:\(\Delta \tau = 1 \, s\);\(v = 5830m/s.\)
- 识别未知事物:\(\Delta t\).
- 将答案表示为方程式:
\[\Delta t = \gamma \Delta \tau = \dfrac{\Delta \tau}{\sqrt{1 - \dfrac{v^2}{c^2}}}. \nonumber \]
- 进行计算。 使用表达式\(\gamma\)来确定来\(\Delta t\)自\(\Delta \tau\):
\[\begin{align*} \Delta t &= \dfrac{1 \, s}{\sqrt{1 - \left(\dfrac{5830 \, m/s}{3.00 \times 10^8 m/s}\right)^2}} \\[4pt] &= 1.000000000189 \, s \\[4pt] &= 1 \, s + 1.89 \times 10^{-10}s. \end{align*} \nonumber \]
意义
HTV-2 的超高速度仍然只有光速的 10 -5 倍。 HTV-2 的相对论效应几乎在所有目的上都可以忽略不计,但不是零。
相对论的速度是多少?
在车辆乘客手表上测量的车辆行驶 1 秒的时间必须有多快,才能使观察者与外面的地面进行测量,相差 1%?
策略
使用时间膨胀公式找出给定倍率的 v/c。
解决方案
- 识别已知的:
\[\dfrac{\Delta \tau}{\Delta t} = \dfrac{1}{1.01}. \nonumber \]
- 识别未知信息:v/c。
- 将答案表示为方程式:
\[ \begin{align*} \Delta t &= \gamma \Delta \tau \\[4pt] &= \dfrac{1}{\sqrt{1 - v^2/c^2}}\Delta \tau \\[4pt] \dfrac{\Delta \tau}{\Delta t} &= \sqrt{1 - v^2/c^2} \\[4pt] \left(\dfrac{\Delta \tau}{\Delta t}\right)^2 &= 1 - \dfrac{v^2}{c^2} \\[4pt] \dfrac{v}{c} &= \sqrt{1 - (\Delta \tau/\Delta t)^2}. \end{align*} \nonumber \]
- 进行计算:
\[\dfrac{v}{c} = \sqrt{1 - (1/1.01)^2} = 0.14. \nonumber \]
意义
结果表明,物体必须以大约光速的10%行进才能产生显著的相对论时间膨胀效应。
\(\Delta t\)计算相对论事件
假设宇宙射线与地球高层大气中的原子核碰撞会产生具有一定速度的μ子\(v = 0.950c\)。 然后,μ子以恒定速度移动,根据μ子的参考系测量,寿命为2.20微秒。 (你可以想象这是介子的内部时钟。) 根据地球观测者的测量,μ子能活多久(图\(\PageIndex{2}\))?
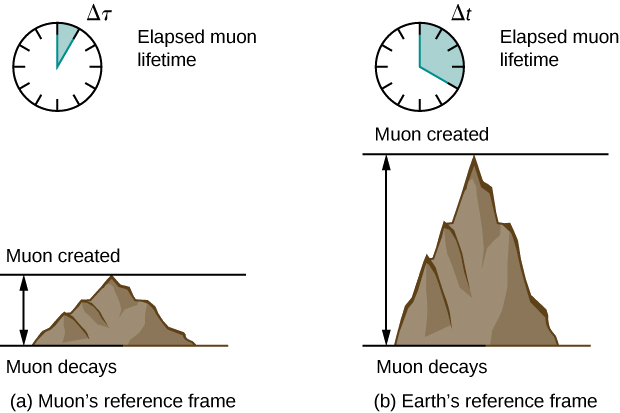
正如我们稍后将讨论的那样,在μ子的参考系中,它的行进距离比在地球参考系中测得的要短。
策略
随μ子移动的时钟测量其衰减过程的正确时间,所以给出的时间是\(\Delta \tau = 2.20 \mu s\)。 地球观测器的测量\(\Delta t\)结果由方程式给出\(\Delta t = \gamma \Delta \tau\)。 因为速度是给定的,所以我们可以在地球的参考系中计算时间。
解决方案
- 识别已知数:\(v = 0.950c\);\(\delta \tau = 2.20 \mu s\).
- 识别未知事物:\(\Delta t\).
- 将答案表示为方程式。 使用:
\[\Delta t = \gamma \Delta \tau. \nonumber \]
和\[\gamma = \dfrac{1}{\sqrt{1 - \dfrac{v^2}{c^2}}}. \nonumber \]
- 进行计算。 使用表达式\(\gamma\)来确定来\(\Delta t\)自\(\Delta \tau\):
\[\begin{align*} \Delta t &= \gamma \Delta \tau. \\[4pt] &=\dfrac{1}{\sqrt{1 - \dfrac{v^2}{c^2}}}\delta \tau \\[4pt] &=\dfrac{2.20 \mu s}{\sqrt{1 - (0.950)^2}} \\[4pt] &= 7.05 \, \mu s.\end{align*} \nonumber \]
记得在最终答案之前保留额外的重要数字。
意义
这个例子的一个含义是,因为\(\gamma = 3.20\)在光速的95.0%(\(v = 0.950c\))下,相对论效应是显著的。 这两个时间间隔相差3.20,而通常它们是相同的。 据说在0.950 c 处移动的东西是高度相对论的。
非平面屏幕、老式电视显示器(图\(\PageIndex{3}\))的工作原理是将电子在短距离内加速到相对论速度,然后使用电磁场控制电子束撞击管前部荧光层的位置。 假设电子从光束起点\(6.00 \times 10^7 m/s\)穿过 0.200m0.200 米的距离到达屏幕。
- 电子在电视机剩余帧中的传播时间是多少?
- 电子在其自身的静止帧中的行进时间是多少?
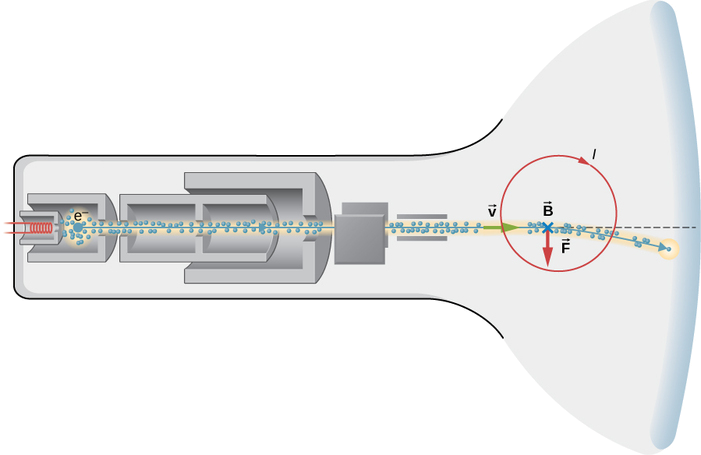
(a) 的战略
(a) 计算起始时间\(vt = d\)。 尽管速度是相对论的,但计算完全在一个参考框架内,因此不涉及相对论。
解决方案
- 识别已知数:
\[v = 6.00 \times 10^7 m/s \, d = 0.200 \, m. \nonumber \]
- 识别未知事物:旅行时间\(\Delta t\)。
- 将答案表示为方程式:
\[\Delta t = \dfrac{d}{v}. \nonumber \]
- 进行计算:
\[ \begin{align*} t &= \dfrac{0.200 \, m}{6.00 \times 10^7 \, m/s} \\[4pt] &= 3.33 \times 10^{-9} \, s. \end{align*} \nonumber \]
意义
正如预期的那样,旅行时间非常短。 由于计算完全在单一参考框架内进行,因此不涉及相对论,尽管电子速度接近 c。
(b) 的战略
(b) 在电子的参照系中,真空管在移动,电子处于静止状态。 电子发射阴极离开电子,真空管的正面撞击电子,电子位于同一位置。 因此,我们使用时间膨胀公式将电子静止帧中的正确时间与电视帧中的时间联系起来。
解决方案
- 识别已知数(来自 a 部分):
\[\Delta t = 3.33 \times 10^{-9} \, s; \, v = 6.00 \times 10^7 \, m/s; \, d = 0.200 \, m. \nonumber \]
- 识别未知事物:\(\tau\).
- 将答案表示为方程式:
\[\Delta t = \gamma \Delta \tau = \dfrac{\Delta \tau}{\sqrt{1 - v^2/c^2}}. \nonumber \]
- 进行计算:
\[\begin{align*} \Delta \tau &= (3.33 \times 10^{-9}s)\sqrt{1 - \left(\dfrac{6.00 \times 10^7 m/s}{3.00 \times 10^8 m/s}\right)^2} \\[4pt] &= 3.26 \times 10^{-9}s. \end{align*} \nonumber \]
意义
在电子参照系中,行程时间较短。 由于问题需要找到在同一过程的不同参考系中测量的时间间隔,因此涉及相对论。 如果我们试图通过简单地将0.200 m除以速度来计算电子静止帧中的时间,则由于电子的相对论速度,结果会稍微不正确。
\(\gamma\)如果会怎\(v = 0.650c\)样?
- 回答
-
\[\gamma = \dfrac{1}{\sqrt{1 - \dfrac{v^2}{c^2}}} = \dfrac{1}{\sqrt{1 - \dfrac{(0.650c)}{c^2}}} = 1.32 \nonumber \]
双胞胎悖论
时间扩张的一个有趣后果是,相对于地球高速移动的太空旅行者的年龄要小于宇航员在地球上的双胞胎。 这通常被称为双胞胎悖论。 想象一下宇航员以如此快的速度移动\(\gamma = 30.0\),如图所示\(\PageIndex{4}\)。 在 Earthbound Twin 的框架中,一次需要 2.00 年的旅行将需要 60.0 年。 假设宇航员在1.00年内前往另一个恒星系统,短暂探索该区域,然后在1.00年前旅行。 当太空飞船返回时,在旅行开始时年满40岁的宇航员将年满42岁。 但是,地球上的一切都将老化60.0年。 地球上的双胞胎如果还活着,将已经 100 岁了。
情况似乎与图中的宇航员不同\(\PageIndex{4}\)。 因为运动是相对的,所以太空飞船似乎是静止的,而地球似乎在移动。 (这是你乘坐喷气式飞机飞行时的感觉。) 看着太空飞船的窗外,宇航员会看到地球上的时间减慢了一倍\(\gamma = 30.0\)。 从太空飞船上看,在地球上的兄弟姐妹的年龄仅为一年的2/30或0.07,而宇航员的年龄将为2.00岁。
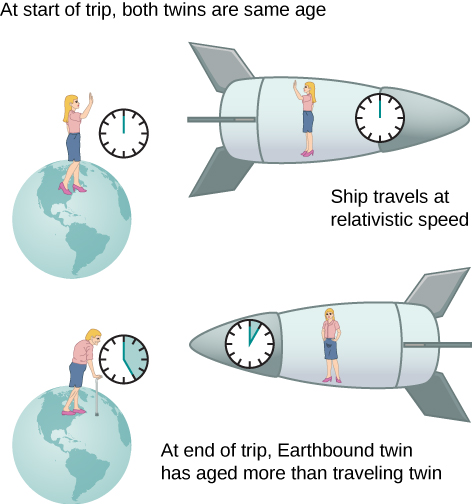
这里的矛盾之处在于,这两个双胞胎不可能都是对的。 与所有悖论一样,相互矛盾的结论来自错误的前提。 实际上,宇航员的动作与地面双胞胎的动作有很大不同。 宇航员加速到高速,然后减速以查看恒星系统。 为了返回地球,她再次加速和减速。 航天器不在可以直接应用时间膨胀公式的单一惯性框架中。 也就是说,宇航员双胞胎改变了惯性基准。 Earthbound 双胞胎不会经历这些加速,而是保持在同一个惯性框架中。 因此,情况并不对称,声称宇航员观察到的效果与她的双胞胎相同,这是不正确的。 当我们在本章后面从宇航员穿越四维时空的路径来分析旅程时,双胞胎之间缺乏对称性将更加明显。
1971年,美国物理学家约瑟夫·哈菲勒和理查德·基廷通过在商用飞机上在世界各地飞行极其精确的原子钟,证实了相对较低速度下的时间膨胀。 他们以几纳秒的精度测量了经过的时间,并将其与剩余时钟测得的时间进行了比较。 哈菲勒和基廷的结果在相对论预测的实验不确定性范围内。 必须同时考虑狭义相对论和广义相对论,因为涉及重力和加速度以及相对运动。
a. 粒子在静止\(2.1 \times 10^8 \, s\)时相对于观察者移动\(1.90 \times 10^8 \, m/s\)并存活。 在实验室中观察到的粒子能存活多久?
- 回答
-
\[\Delta t = \dfrac{\Delta \tau}{\sqrt{1 - \dfrac{v^2}{c^2}}} = \dfrac{2.10 \times 10^{-8}s}{\sqrt{1 - \dfrac{(1.90 \times 10^8 \, m/s)^2}{(3.00 \times 10^8 \, m/s)^2}}} = 2.71 \times 10^{-8} \, s. \nonumber \]
航天器 A 和 B 以相反的方向通过,相对速度为\(4.00 \times 10^7 \, m/s\)。 航天器 A 中的内部时钟使其发出 1.00 秒的无线电信号。航天器 B 中的计算机校正信号行进不同距离的开始和结束,以计算飞船 A 发射信号的时间间隔。 航天器 B 中的计算机计算的时间间隔是多少?
- 回答
-
只有两艘航天器的相对速度才重要,因为在太空中没有绝对的运动。 信号是从 A 的参考系中的固定位置发射的,因此其发射的时间间隔是正确的\(\tau = 1.00 \, s\)。 然后,从参考框架 B 测量的信号持续时间为
\[\Delta t = \dfrac{\Delta \tau}{\sqrt{1 - \dfrac{v^2}{c^2}}} = \dfrac{1.00 \, s}{\sqrt{1 - \dfrac{(4.00 \times 10^7 \, m/s)^2}{(3.00 \times 10^8 \, m/s)^2}}} = 1.01 \, s. \nonumber \]


