5.3: 同时性的相对论

Last updated
Save as PDF

Page ID: 202069

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

学习目标

在本节结束时，您将能够：

从爱因斯坦的假设中可以看出，在一个惯性帧中同时测量的两个事件不一定在所有惯性帧中同时测量。
描述同时性对于处于相对运动的不同惯性帧中的观察者来说是一个相对概念。

时间间隔是否取决于谁观察它们？直观地说，对于所有观察者来说，一个过程的时间，例如徒步比赛的经过时间（图\(\PageIndex{1}\)），似乎应该是相同的。在日常体验中，关于时间流逝的分歧与测量时间的准确性有关。没有人会争辩说移动跑步者的实际时间间隔和显示的固定时钟的实际时间间隔是不同的。但是，仔细考虑如何测量时间，可以看出，经过的时间确实取决于观察者相对于所测量过程的相对运动。

一张徒步比赛结束的照片，显示的是越过终点线的赛车手的时间 43:06。 — 图\(\PageIndex{1}\)：对于所有观察者来说，徒步比赛所经过的时间是相同的，但是在相对论的速度下，经过的时间取决于观察者相对于计时过程发生位置的运动。（来源：“杰森·爱德华·斯科特·贝恩” /Flickr）

考虑一下我们如何衡量经过的时间。例如，如果我们使用秒表，我们怎么知道何时启动和停止手表？一种方法是利用来自事件的光线的到来。例如，如果你在行驶中的汽车中，观察到交通信号灯发出的灯从绿色变为红色，你就知道是时候踏上刹车踏板了。如果使用某种电子检测，则计时会更准确，从而避免人为反应时间和其他并发症。

现在假设两个观察者使用这种方法来测量相隔一定距离的闪光灯发出的两次闪光之间的时间间隔（图\(\PageIndex{2}\)）。观察者 A 坐在轨道车辆的中途，两侧有两个闪光灯与她等距。每个闪光灯发出一个光脉冲并朝观察者 A 移动，如图 (a) 帧所示。轨道车辆正朝图中速度矢量所示的方向快速移动。站在平台上的观察者 B 在轨道车辆经过时正面对轨道车辆，观察到两个闪光同时到达他，如框架 (c) 所示。他测量了与他看到脉冲起源地的距离，发现脉冲相等，并得出结论，脉冲是同时发射的。

但是，由于观察者 A 的运动，来自轨道车辆右侧、汽车移动方向的脉冲在左侧脉冲之前到达她，如第 (b) 帧所示。她还测量了与参考范围内的距离，发现它们相等，并得出结论，脉冲不是同时发射的。

两位观察员就在相隔较远的地点发生的两起事件是否同时发生得出了相互矛盾的结论。这两个参考框架都是有效的，两个结论都是有效的。不同地点的两个事件是否同时发生取决于观察者相对于事件位置的运动。

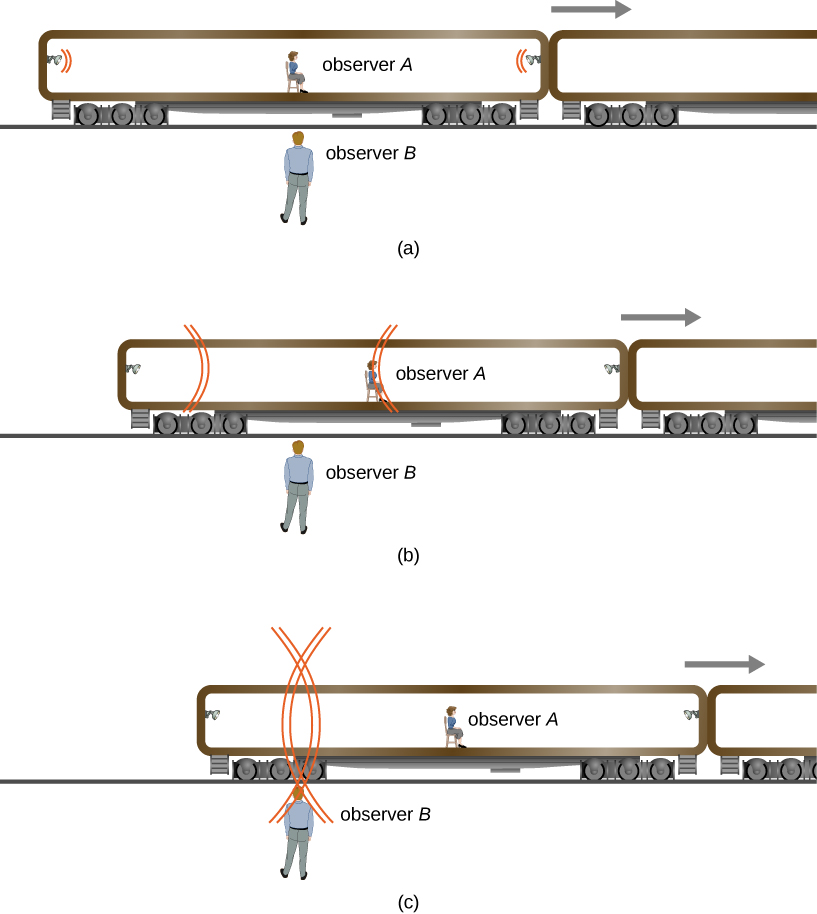
这幅插图显示了一辆火车车厢向右移动，观察者 A 位于车厢中央，两端都有闪光灯。观察者 B 静止地站在外面的地面上。在图 a 中，观察者 A 位于观察者 B 的正前方，闪光灯信号位于火车车厢的两端。在图 b 中，火车向右移动，因此观察者 A 位于观察者 B 的右边。汽车的左端仍在观察者 B 的左边。汽车左端闪光灯发出的信号位于闪光灯和观察者 B 之间。来自汽车右端闪光灯的信号位于观察者 A 的位置。在图 c 中，带有观察点 A 的汽车向右移动。汽车的左端仍在观察者 B 的左边。两个闪光灯信号都在观察者 B 的位置。 — 图\(\PageIndex{2}\)：(a) 相对于观察者 B 同时发射两个光脉冲。(c) 脉冲同时到达观察者 B 的位置。 (b) 由于 A 的运动，她首先看到右边的脉冲，并得出结论，灯泡没有同时闪烁。这两个结论都是正确的。

在这里，观察者之间的相对速度会影响观察到相隔一段距离的两个事件是否同时发生。 同时性不是绝对的。我们可能已经（错误地）猜到，如果光线同时发射，那么两个位于光源中间的观察者将同时看到闪光。但是仔细的分析表明，如果所有惯性帧中的光速都相同，情况就不可能如此。

这种类型的思想实验（德语为 “GedankenExperiment”）表明，必须改变看似显而易见的结论，才能与相对论的假设一致。思想实验的有效性只能通过实际观察来确定，而仔细的实验反复证实了爱因斯坦的相对论。