Skip to main content
Global

15.E：振荡（练习）

  1. Last updated
  2. Save as PDF
  • Page ID
    205019

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    问题

    15.1 简单谐波运动

    1. 证明使用 x (t) = Asin (\(\omega\)t +\(\phi\)) 将在质量和弹簧的振荡周期内产生相同的结果。 你认为为什么选择余弦函数？
    2. 60.0 Hz 的电力周期是多少？
    3. 如果在剧烈运动中你的心率是每分钟 150 次，那么以秒为单位的每跳时间是多少？
    4. 找出音叉的频率，该频率需要 2.50 x 10 −3 秒才能完成一次振荡。
    5. 闪光镜设置为每 8.00 x 10 −5 秒闪烁一次。闪光频率是多少？
    6. 轮胎有胎面花纹，每隔 2.00 cm 就有一条缝隙。 当轮胎移动时，每个缝隙都会产生一次振动。 如果汽车以 30.0 m/s 的速度行驶，这些振动的频率是多少？
    7. 发动机的每个活塞每转一圈就会发出尖锐的声音。 (a) 鉴于发动机每公里转2000转，如果其八缸发动机发出频率为750 Hz的声音，那么赛车的行驶速度有多快？ (b) 发动机以每分钟多少转的速度旋转？
    8. 一种布谷鸟钟通过在弹簧上弹起质量来保持时间，通常像椅子上的小天使一样可爱。 为 0.0150 千克的质量产生 0.500 秒的周期需要多大的力常数？
    9. 质量 m 0 附着在弹簧上并垂直悬挂。 质量在垂直方向上升一小段距离并释放。 质量以 0 的频率振荡。 如果质量被大于九倍的质量所取代，然后重复实验，那么以 f 0 计算，振荡的频率会是多少？
    10. 悬浮在弹簧上的 0.500 千克质量会在 1.50 秒的周期内振荡。必须向物体添加多少质量才能将周期更改为 2.00 秒？
    11. 如果你不希望新周期大于 2.01 秒或小于 1.99 秒，那么在选择上一个问题中物体的质量时你还有多少余地（包括百分比和质量）？

    15.2 简单谐波运动中的能量

    1. 鱼被悬挂在弹簧尺上，以确定它们的重量。 (a) 如果弹簧在 10.0 kg 的负载下延伸 8.00 cm，那么这种比例下弹簧的力常数是多少？ (b) 一条延伸弹簧5.50厘米的鱼的质量是多少？ (c) 体重秤上的半千克标记相距多远？
    2. 对于当地85公斤以下的橄榄球队来说，现在是称重的时候了。 用于评估资格的浴室秤可以用胡克定律来描述，最大负荷为120 kg，下调0.75厘米。 (a) 弹簧的有效力常数是多少？ (b) 玩家站在体重秤上并将其压低0.48厘米。 他有资格参加这支85公斤以下的球队吗？
    3. 一种 BB 枪使用弹簧驱动的柱塞将 BB 从枪管中吹出。 (a) 如果必须将其压缩 0.150 m 才能将 0.0500 kg 的柱塞驱动到 20.0 m/s 的最高速度，请计算其柱塞弹簧的力常数。(b) 必须施加什么力才能压缩弹簧？
    4. 当一个 80.0 公斤的人站在弹簧棒上时，弹簧被压缩 0.120 m。(a) 弹簧的力常数是多少？ (b) 当他跳下路时，弹簧会被压缩得更多吗？
    5. 当弹簧悬挂着0.300千克的质量时，弹簧的长度为0.200 m；当悬挂在弹簧上的质量为1.95千克时，其长度为0.750米。 (a) 弹簧的力常数是多少？ (b) 弹簧的空载长度是多少？
    6. 登山者悬挂的尼龙绳的有效力常数为 1.40 x 10 4 N/m。(a) 鉴于他的质量加上和装备的质量为 90.0 kg，他弹跳的频率是多少？ (b) 如果登山者在绳索用完之前自由落下 2.00 米，这根绳子会伸出多少才能打破他的跌落？ （提示：使用节能。） (c) 在使用两倍长度的尼龙绳的情况下，重复这个问题的两个部分。

    15.3 比较简单谐波运动和圆周运动

    1. 也可以使用旋转圆盘对弹簧上垂直悬挂的质量块的运动进行建模，质量在弹簧上下振荡。 与其将灯光沿顶部水平放置并指向下方，不如垂直放置灯光，让灯光照在旋转圆盘的侧面。 将在附近的墙上产生阴影，并将上下移动。 写下阴影的运动方程，以 t = 0.0 s 的位置为 y = 0.0 m，质量沿正 y 方向移动。
    2. (a) 新颖的时钟有一个 0.0100 千克质量的物体在弹簧上弹跳，弹簧的力常数为 1.25 N/ m。如果物体在其平衡位置上方和下方反弹 3.00 厘米，该物体的最大速度是多少？ (b) 物体在最大速度下有多少焦耳的动能？
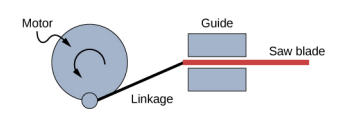
    3. 往复运动使用电动机的旋转来产生上下或来回的线性运动。 这就是往复锯的工作方式，如下所示。 如果电机以 60 Hz 旋转且半径为 3.0 cm，则估计锯片上下移动时的最大速度。 这种设计被称为苏格兰枷锁。

    电机的示意图，描绘成圆盘在其轴线上旋转，导致锯片水平移动。 马达盘的底部是一个与水平叶片相连的连杆。 连杆可以在两端旋转。 刀片被导向块中的水平间隙限制在水平方向移动。

    1. 一个学生站在旋转木马的边缘，旋转木马每分钟旋转五次，有一天晚上太阳落山时半径为两米。 学生在附近的建筑物上制造阴影。 (a) 为阴影的位置写一个方程式。 (b) 写一个阴影速度的方程式。

    15.4 钟摆

    1. 周期为 0.500 秒的钟摆的长度是多少？
    2. 有些人认为，周期为1.00秒的钟摆可以用 “精神能量” 或心理动力学来驱动，因为它的周期与平均心跳相同。 对与否，这种钟摆的长度是多少？
    3. 1.00 米长的钟摆周期是多少？
    4. 如果孩子的重心位于枢轴以下 4.00 m 处，那么在秋千上完成一次挥杆需要多长时间？
    5. 布谷鸟钟上的钟摆长 5.00 厘米。 它的频率是多少？
    6. 两只长尾小鹦鹉坐在秋千上，它们的总长度在枢轴下方 10.0 厘米处。 它们以什么频率摆动？
    7. (a) 周期为 3.00000 秒且位于重力加速度为 9.79 m/s 2 的摆锤移动到重力加速度为 9.8 2 m/s 2 的位置。 它的新时期是什么？ (b) 根据周期与重力加速度之间的关系，解释为什么周期值需要这么多数字。
    8. 一个位置周期为 2.00000 秒（g = 9.80m/s 2）的钟摆被移动到一个新位置，现在周期为 1.99796 秒。由于重力在新位置产生的加速度是多少？
    9. (a) 如果你把钟摆的长度加倍，会对钟摆的周期产生什么影响？ (b) 如果你将钟摆的长度缩短 5.00%，会对钟摆的周期产生什么影响？

    15.5 阻尼振荡

    1. 轻度阻尼振荡器的振幅在每个周期内降低3.0％。 振荡器在每个周期中损失了多少百分比的机械能？

    15.6 强制振荡

    1. 一辆 1200 千克汽车的减震器必须消耗多少能量才能抑制最初在平衡位置速度为 0.800 m/s 的反弹？ 假设汽车返回到其原始垂直位置。
    2. 如果汽车的悬架系统的力常数为 5.00 x 10 4 N/m，则汽车的冲击必须消耗多少能量才能抑制从最大排量为 0.0750 m 开始的振荡？
    3. (a) 当弹簧一动不动地悬挂在弹簧上时，力常数为 40.0 N/m 的弹簧会被质量为 0.500 kg 的物体拉伸多少？ (b) 计算0.500-kg物体下降该距离时引力势能的减少情况。 (c) 这种引力的一部分进入弹簧。 计算该拉伸时弹簧中储存的能量，并将其与引力势能进行比较。 解释剩下的能量可能去哪里。
    4. 假设您在水平表面上有一个 0.750 千克的物体连接到力常数为 150 N/m 的弹簧。物体和表面之间存在简单的摩擦力，静摩擦系数\(\mu_{s}\) = 0.100。 (a) 在不移动物体的情况下，弹簧可以拉伸多远？ (b) 如果物体处于振荡状态，振幅是 (a) 部分中距离的两倍，并且动摩擦系数为\(\mu_{k}\) = 0.0850，则它在停止之前的总行驶距离是多少？ 假设它从最大振幅开始。

    其他问题

    1. 假设你将一个质量为 m 的物体连接到最初处于静止状态的垂直弹簧上，然后让它上下弹跳。 你可以在弹簧的原始静止长度上释放物体，即弹簧处于平衡状态的长度，而不附着质量。 运动的振幅是指未附着质量的弹簧的平衡位置与附着质量的弹簧的平衡位置之间的距离。 (a) 显示弹簧在物体的最低点施加2.00mg的向上力。 (b) 如果弹簧的力常数为 10.0 N/m，水平悬挂，弹簧自由端的位置标记为 y = 0.00 m，那么如果弹簧上悬挂一个 0.25 千克质量的物体，新的平衡位置在哪里？ (c) 如果弹簧的力常数为10.0 m/m，并且质量为0.25千克的物体如上所述开始运动，则找出振荡的振幅。 (d) 找到最大速度。
    2. 跳水板上的一名潜水员正在进行 SHM。 她的体重为 55.0 kg，运动周期为 0.800 秒。下一个潜水员是男性，其简单谐波振荡周期为 1.05 秒。如果滑板的质量可以忽略不计，他的质量是多少？
    3. 频率为 4.00 赫兹。 该板的有效质量为10.0 kg。 一名 75.0 公斤的潜水员在船上使用 SHM 的频率是多少？
    4. 下图所示的设备在招待婴儿的同时防止他们流浪。 孩子用弹簧悬挂在门框上的安全带里弹跳。 (a) 如果弹簧在支撑一个 8.0 公斤的孩子的同时伸展 0.250 米，它的力常数是多少？ (b) 这个孩子什么时候能完全弹跳？ (c) 如果孩子的弹跳幅度为 0.200 m，她的最大速度是多少？
    一张穿着悬挂式摇椅的婴儿的照片。
    图 15.E.34（来源：丽莎·多纳特）
    1. 质量物放置在无摩擦的水平工作台上。 桌子上放置了一个可以拉伸或压缩的弹簧（k = 100 N/m）。 5.00 kg 的质量附着在弹簧的一端，另一端固定在墙上。 平衡位置标记为零。 学生将肿块移至 x = 4.0 cm，然后将其从静止状态中释放。 质量在 SHM 中振荡。 (a) 确定运动方程。 (b) 找出时间 t = 3.00 秒时质量的位置、速度和加速度。
    2. 如果钟摆从地球运送到月球，则求出摆锤新旧周期的比率，其中重力产生的加速度为1.63 m/s 2。
    3. 如果钟精确地保持地球上的时间，摆钟在月球上运行的速度是多少，重力引起的加速度为1.63 m/s 2？ 也就是说，找出时钟的时针在月球上旋转一圈所花费的时间（以小时为单位）。
    4. 如果摆锤驱动的时钟每天增益 5.00，则必须对摆锤长度进行多少小数变化才能保持完美时间？
    5. 一个 2.00 千克的物体静止时悬挂在天花板上的 1.00 米长的绳子上。 100克的质量在2.00千克的质量下以20 m/s的速度发射，而100.00克的质量与2.00千克的质量完美弹性碰撞。 写一个碰撞后悬挂物体运动的方程式。 假设空气阻力可以忽略不计。
    6. 一个 2.00 千克的物体静止时悬挂在天花板上的 1.00 米长的绳子上。 一个 100 g 的物体以 20 m/s 的速度向 2.00 千克的物体发射，两个物体在完全没有弹性的碰撞中碰撞并粘在一起。 写一个碰撞后系统运动的方程式。 假设空气阻力可以忽略不计。
    7. 假设用于驱动祖父钟的钟摆的长度为 L 0 = 1.00 m，在温度 T = 20.00°C 时质量为 M。它可以建模为围绕一端振荡的杆形的物理摆锤。 如果温度升高10°C，周期会改变多少百分比？ 假设棒的长度随温度呈线性变化，其中 L = L 0 (1 +\(\alpha \Delta\) T)，杆由黄铜制成（\(\alpha\)= 18 x 10 −6 °C −1）。
    8. 一个 2.00 千克的方块静止在无摩擦的桌子上。 弹簧常数为 100 N/m 的弹簧连接到墙壁和方块上。 第二个重量为 0.50 kg 的方块放在第一个方块的顶部。 2.00 千克的方块被轻轻拉到 x = + A 的位置，然后从静止状态中释放。 两个方块之间的摩擦系数为 0.45。 (a) 振荡周期是多久？ (b) 允许方块在不滑落 0.50 千克方块的情况下振荡的最大运动幅度是多少？

    挑战问题

    1. 悬索桥振荡的有效力常数为 1.00 x 10 8 N/m。(a) 使其振幅为 0.100 m 需要多少能量？ (b) 如果士兵以等于桥的自然频率的节奏穿过桥梁，每秒传递1.00 x 10 4 J的能量，则桥的振幅从0.100 m变为0.500 m需要多长时间。
    2. 在纽约市花旗集团中心大楼顶部附近，弹簧上有一个质量为 4.00 x 10 5 kg 的物体，弹簧的力常数可调。 它的功能是通过以与建筑物被驱动的相同频率振荡来抑制建筑物的风力驱动的振动——驱动力被传递到物体上，物体会振荡而不是整个建筑物。 (a) 弹簧必须有多大的有效力常数才能使物体在 2.00 秒的周期内振荡？ (b) 弹簧中储存了什么能量才能偏离平衡 2.00 米？
    3. 由于航空包裹的浮力所提供的恢复力，在稳定的大气层（温度随高度升高）中的空气包裹（少量空气）可以上下振荡。 振荡频率是衡量大气稳定性的指标。 假设航空包裹的加速度可以建模为\(\frac{\partial^{2} z}{\partial t^{2}} = \frac{g \partial \rho (z)}{\rho_{0} \partial z} z'\)，证明\(z' = z'_{0} e^{t \sqrt{-N^{2}}}\)这是一个解决方案，其中 N 被称为 Brunt-Väisälä频率。 请注意，在稳定的大气中，密度随高度而降低，包裹上下振荡。
    4. 以范德华电位 U (r) = U 0 为例\(\Bigg[ \left(\dfrac{R_{0}}{r}\right)^{2} - 2 \left(\dfrac{R_{0}}{r}\right)^{6} \Bigg] \)，用于模拟两个分子的势能函数，其中最小电位为 r = R 0。 求力作为 r 的函数。考虑一个小位移 r = R 0 + r′ 并使用二项式定理：$$ (1 + x) ^ {n} = 1 + nx +\ frac {n (n-1)} {2!} x^ {2} +\ frac {n (n-1) (n-2)} {3!} x^ {3} +\ cdots$$，以表明该力确实接近胡克定律力。
    5. 假设时钟摆的长度变化了 1.000%，恰好是在某一天的中午。 假设钟摆在变更之前一直保持完美时间，24.00 小时后什么时候读取？ 请注意，有两个答案，并以四位数的精度进行计算。
    6. (a) 皮卡车的弹簧就像单弹簧一样，力常数为 1.30 x 10 5 N/m。卡车的最大载荷为 1000 kg 会受到多大的压力？ (b) 如果皮卡车有四个相同的弹簧，每个弹簧的力常数是多少？