15.7：强制振荡

Last updated
Save as PDF

Page ID: 205040

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

学习目标

定义强制振荡
列出与强制振荡相关的运动方程
解释共振的概念及其对振荡器振幅的影响
列出在共振中振荡的系统的特性

有时候坐在钢琴前，用琴弦上的阻尼器对着钢琴大声唱一首简短的音符（图\(\PageIndex{1}\)）。它会向你唱同样的音符 —— 与你的声音具有相同频率的弦乐会产生共鸣，以响应你发送给它们的声波产生的力。这是一个很好的例子，说明物体（在本例中为钢琴弦）可以被迫振荡，并且最容易以其自然频率振荡。在本节中，我们将简要探讨施加周期性驱动力作用于简单的谐波振荡器。驱动力以一定的频率将能量注入系统，不一定与系统的自然频率相同。回想一下，自然频率是指在没有驱动力和阻尼力的情况下系统振荡的频率。

一张钢琴弦的特写照片 — 图\(\PageIndex{1}\)：-只要从你的声音中产生声波，你就可以使钢琴中的琴弦振动。

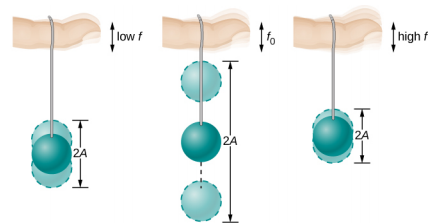
我们大多数人都玩过涉及支撑在松紧带上的物体的玩具，比如人物中悬挂在手指上的桨球\(\PageIndex{2}\)。想象一下图中的手指就是你的手指。首先，你用手指保持稳定，球会在少量阻尼的情况下上下弹跳。如果你缓慢地上下移动手指，球会随之移动，不会自行弹得太多。当你增加上下移动手指的频率时，球的反应是以越来越大的振幅振荡。当你以固有频率驱动球时，只要你开球，球的振荡幅度就会随着每次振荡而增加。以等于其自然频率的频率驱动系统的现象称为共振。据说以自然频率驱动的系统会产生共鸣。随着驱动频率逐渐高于共振频率或自然频率，振荡的振幅会变小，直到振荡几乎消失，而你的手指只是上下移动，对球的影响很小。

该图显示了三张横向观察的照片，其中一根绳子悬挂在手指上，一根球绑在它的下端。在第一张图中，手指以低频率 f 上下移动，球在距离其平衡高度有一段距离的地方上下移动，图中的位移显示为球的褪色阴影，平衡位置显示为较暗的图像。在第二张图中，手指以低于零的频率上下移动，球的移动比第一张图大得多。在第三张图中，手指以高频率 f 上下移动，球的移动小于第一张图中的移动。在所有三个数字中，球从最低位置到最高位置的总距离都表示为 2 A。 — 图\(\PageIndex{2}\)：橡皮筋上的桨球随着支撑它的手指而移动。如果手指以橡皮筋上球的固有频率 f0 移动，则会产生共振，球的振荡幅度会急剧增加。在越来越高的驱动频率下，能量传递给球的效率会降低，并且球会以较低的振幅振荡做出响应。

考虑一个简单的实验。将质量 m 连接到粘性流体中的弹簧上，类似于阻尼谐波振荡器中讨论的设备。这次，与其固定弹簧的自由端，不如将自由端连接到由变速电机驱动的圆盘上。电动机转动的角驱动频率为 Ω。旋转盘通过驱动力（F _d = F ₀ sin (\(\omega\)t)）所做的工作为系统提供能量。实验设备如图所示\(\PageIndex{3}\)。

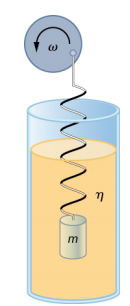
质量 m 悬浮在垂直弹簧上，然后浸入粘度为 eta 的流体中。弹簧的顶部连接到垂直圆盘的边缘，该盘在水平轴上旋转，角速度为欧米茄。 — 图\(\PageIndex{3}\)：通过使用由变速电机驱动的圆盘驱动弹簧和质量而产生的强制阻尼谐波运动。

使用牛顿第二定律 (\(\vec{F}_{net} = m \vec{a}\))，我们可以分析质量的运动。所得方程与阻尼谐波振荡器的力方程类似，但加上了驱动力：

\[-kx -b \frac{dx}{dt} + F_{0} \sin (\omega t) = m \frac{d^{2} x}{dt^{2}} \ldotp \label{15.27}\]

当用周期性驱动力强制振荡器时，运动可能看起来很混乱。振荡器的运动被称为瞬变。瞬变消失后，振荡器进入稳定状态，运动是周期性的。一段时间后，这个微分方程的稳态解是

\[x(t) = A \cos (\omega t + \phi) \ldotp \label{15.28}\]

再一次，要证明这个方程是一个解，只能作为一种练习。取出 x (t) 的一阶和二阶时间导数并将其代入力方程表明 x (t) = Asin (\(\omega t + \phi\)) 是解，只要振幅等于

\[A = \frac{F_{0}}{\sqrt{m^{2} (\omega^{2} - \omega_{0}^{2})^{2} + b^{2} \omega^{2}}} \label{15.29}\]

其中\(\omega_{0} = \sqrt{\frac{k}{m}}\)是质量和弹簧系统的固有角频率。回想一下，电动机的角频率以及频率是可以调整的。从振幅方程的分母来看，当驱动频率比自然频率小得多或大得多时，两个角频率差的平方为\((\omega^{2} − \omega_{0}^{2})^{2}\)正又大，这使得分母变大，结果是振幅很小质量的振荡。当驱动力的频率接近系统的自然频率时，分母变小，振荡的振幅变大。当驱动力的频率等于系统的自然频率（A _{max =\(\frac{F_{0}}{b \omega}\)）时，会产生最大}振幅。

图中\(\PageIndex{4}\)显示了阻尼谐波振荡器的振幅与驱动它的周期力频率的函数关系。图表上的三条曲线中的每条都代表不同的阻尼量。所有三条曲线在驱动力的频率等于谐波振荡器的自然频率处达到峰值。最高峰值或最大响应是指阻尼量最小，因为阻尼力消耗的能量更少。请注意，由于振幅随着阻尼的减小而增加，因此在没有阻尼的情况下将其设为极限（b = 0），振幅将变为无穷大。

请注意，小振幅驱动力可以产生大振幅响应。这种现象被称为共振。共鸣的一个常见例子是父母在秋千上推小孩。当孩子想走得更高时，父母不会向后移动，然后在开始跑步时，猛击孩子，在短时间内施加很大的力量。相反，父母以恰到好处的频率向孩子施加小推动，孩子挥杆的振幅就会增加。

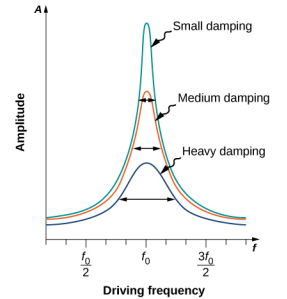
振幅与驱动频率的关系图，显示了小阻尼、中阻尼和重阻尼的曲线。水平轴上标注了 f sub zero 的频率，f sub zero 和 2 之上的三个 f sub zero 的频率。这些曲线是对称的，所有曲线的最大振幅均为零以下。小阻尼曲线具有最大最大值，重阻尼曲线具有最小的最大值。显示了曲线最大值一半的宽度。最窄的曲线是小阻尼曲线，最宽的曲线是重阻尼曲线。 — 图\(\PageIndex{4}\)：谐波振荡器的振幅与驱动力频率的关系。曲线表示相同的振荡器，其固有频率相同，但阻尼量不同。当驱动频率等于自然频率时，就会发生谐振，而最大的响应是阻尼量最小。最窄的响应也适用于最小的阻尼。

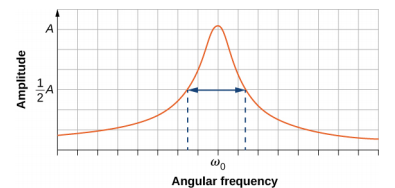
值得注意的是，图中所示的共振曲线的宽度\(\PageIndex{4}\)取决于阻尼：阻尼越小，共振越窄。结果是，如果你想让受驱动振荡器以非常特定的频率产生共振，你需要尽可能少的阻尼。例如，无线电具有用于选择特定广播电台的电路。在这种情况下，强制阻尼振荡器由电阻器、电容器和电感器组成，本课程后面将对此进行讨论。电路被 “调谐” 以选择特定的广播电台。这里希望谐振曲线非常窄，以便找出所选广播电台的确切频率。图表的窄度以及选择一定频率的能力被称为系统的质量。质量定义为角频率的扩散，或等效的频率扩散，以最大振幅的一半除以自然频率 (Q =\(\frac{\Delta \omega}{\omega_{0}}\))，如图所示\(\PageIndex{5}\)。对于较小的阻尼，质量大约等于 Q β\(\frac{2b}{m}\)。

振幅与角频率的关系图。曲线对称且呈峰值，在标记为 omega sub zero 的频率下的最大振幅为 A。表示曲线的宽度，其中最大值两侧的振幅为半A。 — 图\(\PageIndex{5}\)：系统的质量定义为振幅一半的频率分布除以自然频率。

驱动谐波振荡器的这些特性适用于各种各样的系统。例如，磁共振成像（MRI）是一种广泛使用的医学诊断工具，其中原子核（主要是氢核或质子）通过入射无线电波（大约 100 MHz）产生共振。在所有这些情况下，能量从驱动力传递到振荡器的效率在谐振时最好。该图\(\PageIndex{6}\)显示了伦敦千禧人行天桥，该桥允许行人穿越伦敦的泰晤士河。这座桥被昵称为 “Wobbly Bridge”，当时行人在过桥时经历了摇摆的动作。为了摆脱这项动议，这座桥关闭了大约两年。

图片显示了伦敦千禧人行天桥。 — 图\(\PageIndex{6}\)：最初，当人们穿过伦敦千禧人行天桥时，他们经历了摇摆的动作。人们继续交叉强化了振荡的振幅，从而增加了有问题的摇摆。（来源：阿德里安·平斯通/维基共享资源）

练习 15.6

一个著名的魔术是表演者向水晶玻璃唱一张音符，直到玻璃破碎。解释为什么这个技巧在共振和自然频率方面起作用。