15.6: 阻尼振荡

Last updated
Save as PDF

Page ID: 205029

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

学习目标

描述阻尼谐波运动的运动
写出阻尼谐波振荡的运动方程
描述被驱动或强制阻尼谐波运动的运动
写出强制阻尼谐波运动的运动方程

在现实世界中，振荡很少跟随真正的 SHM。某种形式的摩擦通常会抑制运动，使其消失，或者需要更多的力量才能继续。在本节中，我们将研究一些阻尼谐波运动的示例，并了解如何修改运动方程来描述这种更一般的案例。

弹奏几秒钟后，吉他弦停止振动。要继续在游乐场秋千上挥杆，你必须继续推动（图\(\PageIndex{1}\)）。尽管我们经常可以使摩擦力和其他非保守力变小或可以忽略不计，但完全没有阻尼的运动很少见。实际上，我们甚至可能想抑制振荡，例如使用汽车减震器。

秋千上的人的照片 — 图\(\PageIndex{1}\)：为了抵消阻尼力，你需要继续挥杆。（来源：Bob Mical）

图中\(\PageIndex{2}\)显示了附着在弹簧上的质量 m，力常数 k。质量被提升到位置 A ₀，即初始振幅，然后释放。质量在具有粘度的流体中围绕平衡位置振荡，但每次振荡的振幅都会减小。对于具有少量阻尼的系统，周期和频率是恒定的，与 SHM 几乎相同，但振幅逐渐减小，如图所示。之所以出现这种情况，是因为非保守的阻尼力会从系统中移除能量，通常以热能的形式消失。

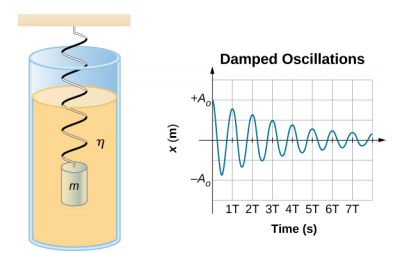
质量 m 悬浮在垂直弹簧上，然后浸入粘度为 eta 的流体中。阻尼振荡的图表显示了垂直轴上的位移 x（以米为单位）与水平轴上的时间函数（以秒为单位）。 x 的范围是从负 A 次零到加 A 子零。时间尺度从 0 到 7 T，抽动以 T 为增量。位移为 A 次零，在正最大值和负最小值之间振荡，每个完整周期的时间 T 相同，但振荡的振幅会随着时间的推移而减小。 — 图\(\PageIndex{2}\)：对于在粘性流体中振荡的弹簧上的质量，周期保持不变，但由于流体造成的阻尼，振荡的振幅会降低。

以作用于群众的力量为例。请注意，权重的唯一贡献是改变均衡位置，如本章前面所述。因此，净力等于弹簧的力和阻尼力 (\(F_D\))。如果速度的大小很小，这意味着质量振荡得很慢，则阻尼力与速度成正比并作用于运动方向 (\(F_D = −b\))。因此，质量上的净力为

\[ma = -bv - kx \ldotp\]

把它写成 x 中的微分方程，我们得到

\[m \frac{d^{2} x}{dt^{2}} + b \frac{dx}{dt} + kx = 0 \ldotp \label{15.23}\]

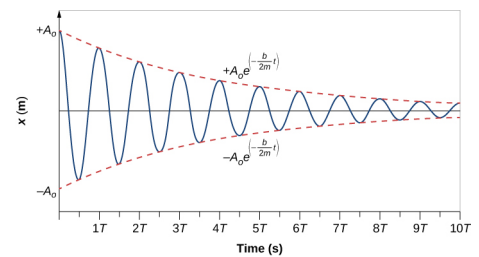
要确定该方程的解，请考虑图中所示的位置与时间关系图\(\PageIndex{3}\)。该曲线类似于在指数函数包络中振荡的余弦曲线，\(A_0e^{−\alpha t}\)其中\(\alpha = \frac{b}{2m}\)。解决的办法是

\[x(t) = A_{0} e^{- \frac{b}{2m} t} \cos (\omega t + \phi) \ldotp \label{15.24}\]

这只能作为一种练习来证明这其实是解决办法。为了证明这是正确的解，请取相对于时间的一阶和二阶导数，并将其替换为方程式15.23。结果发现，方程式 15.24 是解

\[\omega = \sqrt{\frac{k}{m} - \left(\dfrac{b}{2m}\right)^{2}} \ldotp\]

回想一下，经过 SHM 的质量的角频率等于力常数的平方根除以质量。这通常被称为自然角频率，表示为

\[\omega_{0} = \sqrt{\frac{k}{m}} \ldotp \label{15.25}\]

阻尼谐波运动的角频率变为

\[\omega = \sqrt{\omega_{0}^{2} - \left(\dfrac{b}{2m}\right)^{2}} \ldotp \label{15.26}\]

该图显示了沿垂直轴的位移图，以米为单位 x，沿水平轴显示了时间（以秒为单位）。位移范围从负 A 次零到加 A 次零，时间范围从 0 到 10 T。蓝色曲线显示的位移在正最大值和负最小值之间振荡，形成一个波浪，随着我们从 t=0 移动，其振幅逐渐减小。相邻波峰之间的时间 T 始终保持不变。包络线是连接波峰的平滑曲线和连接振荡波谷的另一条平滑曲线，显示为一对红色的虚线。连接波峰的上部曲线被标记为加上 A 次零乘以 e 到数量减去 b t 超过 2 m。连接波谷的下部曲线被标记为减去 A sub 0 乘以 e 到 2 m 以上的量减去 b t。 — 图\(\PageIndex{3}\)：粘性流体中弹簧上质量振荡的位置与时间的关系。请注意，曲线似乎是指数包络内的余弦函数。

回想一下，当我们开始描述阻尼谐波运动时，我们说阻尼必须很小。我想到了两个问题。为什么阻尼必须很小？那么有多小才是小呢？如果您逐渐增加系统中的阻尼量，则周期和频率开始受到影响，因为阻尼与来回运动相反，因此会减慢来回运动的速度。（两个方向的净力都较小。）如果阻尼非常大，系统甚至不会振荡，它会慢慢走向平衡。角频率等于

\[\omega = \sqrt{\frac{k}{m} - \left(\dfrac{b}{2m}\right)^{2}} \ldotp\]

随着 b 的增加，\(\frac{k}{m} - \left(\dfrac{b}{2m}\right)^{2}\)变小并在 b = 时最终变为零\(\sqrt{4mk}\)。如果 b 变大，则\(\frac{k}{m} - \left(\dfrac{b}{2m}\right)^{2}\)变为负数\(\sqrt{\frac{k}{m} - \left(\dfrac{b}{2m}\right)^{2}}\)且为复数。

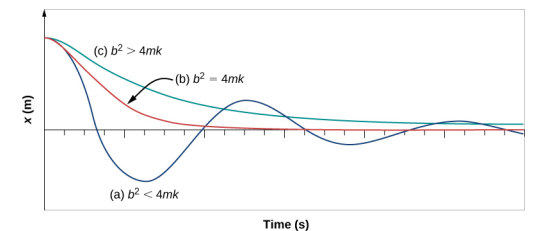
垂直轴上的位置，x（以米为单位），水平轴上的时间（以秒为单位），阻尼程度不同。两个轴均未给出比例。所有三条曲线在时间为零时都从相同的正位置开始。标有 b 平方的蓝色曲线 a 小于 4 m k，振幅减小且周期恒定，振幅略超过四分之一。标有 b 平方的红色曲线 b 等于 4 m k，在 t=0 处的减速速度低于蓝色曲线，但不振荡。红色曲线渐近接近 x=0，在蓝色曲线的一次振荡中几乎为零。标有 b 平方的绿色曲线 c 大于 4 m k，在 t=0 时减小的速度比红色曲线慢，并且不振荡。绿色曲线渐近接近 x=0，但在蓝色曲线振荡两次以上之后，在图表末尾仍明显高于零。 — 图\(\PageIndex{4}\)：由粘性流体中的质量和弹簧组成的三个系统的位置与时间的关系。 (a) 如果阻尼很小 (b <\(\sqrt{4mk}\))，则质量会振荡，随着能量被非保守力消散，振幅会慢慢丧失。极限情况为 (b)，其中阻尼为 (b =\(\sqrt{4mk}\))。 (c) 如果阻尼非常大 (b >\(\sqrt{4mk}\))，则质量在移位时不会振荡，而是尝试恢复到平衡位置。

图中\(\PageIndex{4}\)显示了谐波振荡器在不同阻尼量下的位移。

当阻尼常数 b < 较小时\(\sqrt{4mk}\)，系统会振荡，而运动振幅呈指数级衰减。据说该系统阻尼不足，如曲线 (a) 所示。许多系统阻尼不足，在振幅呈指数级减小的同时振荡，例如质量在弹簧上振荡。阻尼可能很小，但质量最终会停止。
如果阻尼常数为\(b = \sqrt{4mk}\)，则系统被称为临界阻尼，如曲线 (\(b\)) 所示。严重阻尼系统的一个例子是汽车中的减震器。尽可能快地使振荡衰减是有利的。在这里，系统不会振荡，而是尽可能快地渐近地接近平衡状态。
图中的曲线 (c)\(\PageIndex{4}\) 代表过阻尼系统，其中\(b > \sqrt{4mk}\)。过阻的系统将在更长的时间内接近平衡。

通常需要临界阻尼，因为这样的系统会迅速恢复平衡并保持平衡。此外，施加于临界阻尼系统的恒定力可在尽可能短的时间内将系统移动到新的平衡位置，而不会在新的位置上过冲或振荡。

练习\(\PageIndex{1}\)

为什么完全无阻尼的谐波振荡器如此罕见？