15.5: 钟摆

Last updated
Save as PDF

Page ID: 204997

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

学习目标

陈述作用于简单钟摆的力
根据摆的长度和重力引起的加速度来确定简单摆的角频率、频率和周期
定义物理摆的周期
定义扭摆的周期

钟摆是常见的用法。祖父钟使用钟摆来保持时间，钟摆可以用来测量重力引起的加速度。对于小位移，摆锤是一种简单的谐波振荡器。

简单摆锤

简单摆锤被定义为具有点质量，也称为摆锤，它悬挂在一根长度为 L 的绳子上，质量可以忽略不计（图$\PageIndex{1}$）。在这里，作用于鲍勃的唯一力量是重力（即鲍勃的重量）和来自绳子的张力。假定弦的质量与鲍勃的质量相比可以忽略不计。

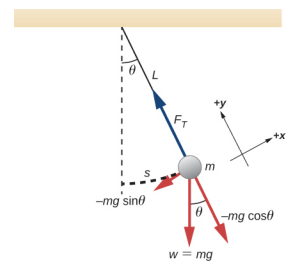
图中显示了一条水平条。一根长度为 L 的绳子从钢筋向垂直方向逆时针方向以 theta 的角度延伸。垂直方向由一条虚线指示，该虚线从字符串连接到钢筋的位置向下延伸。绳子的下端附着一个质量为 m 的圆形鲍勃。从质量到垂直方向的弧线由另一条虚线表示，长度为 s。沿着向小节的弦线显示一个表示生物振荡时间 T 的红色箭头。在鲍勃附近显示了一个坐标系，其正 y 方向与字符串对齐并指向枢轴点，正的 x 方向指向与弧线切线并远离平衡位置。沿着弦从鲍勃向枢轴方向的蓝色箭头标记为 F sub T。从鲍勃向下指向下的红色箭头标记为 w = m g。红色箭头在负 x 方向上指向与弧线切线并指向平衡，标记为负 m g sine theta。从 w 逆时针方向成一定角度 theta 的红色箭头被标记为减去 m g 余弦 theta。 — 图$\PageIndex{1}$：一个简单的摆锤有一个直径很小的摆锤和一根质量很小但足够坚固的绳子，无法明显伸展。平衡的线性位移为 s，即电弧的长度。还显示了鲍勃上的力，它产生了$\theta$朝向平衡位置的净力 −mgsin，即恢复力。

以钟摆上的扭矩为例。提供恢复扭矩的力是沿弧长作用的摆锤重量的组成部分。扭矩是弦的长度 L 乘以垂直于电弧半径的净力分量。减号表示扭矩的作用方向与角位移相反：

\[\begin{split} \tau & = -L (mg \sin \theta); \\ I \alpha & = -L (mg \sin \theta); \\ I \frac{d^{2} \theta}{dt^{2}} & = -L (mg \sin \theta); \\ mL^{2} \frac{d^{2} \theta}{dt^{2}} & = -L (mg \sin \theta); \\ \frac{d^{2} \theta}{dt^{2}} & = - \frac{g}{L} \sin \theta \ldotp \end{split}\]

这个微分方程的解涉及高级微积分，超出了本文的范围。但请注意，对于小角度（小于 15°），sin$\theta$ 和 sin$\theta$ 相差小于 1%，因此我们可以使用小角度近似值 sin$\theta$ β$\theta$。角度$\theta$描述了钟摆的位置。使用小角度近似值可以得出小角度的近似解，

\[\frac{d^{2} \theta}{dt^{2}} = - \frac{g}{L} \theta \ldotp \label{15.17}\]

由于该方程与 SHM 方程的形式相同，因此很容易找到解。角频率是

\[\omega = \sqrt{\frac{g}{L}} \label{15.18}\]

而这个周期是

\[T = 2 \pi \sqrt{\frac{L}{g}} \ldotp \label{15.19}\]

简单摆锤的周期取决于其长度和重力引起的加速度。该周期完全不受其他因素的影响，例如质量和最大位移。与简单的谐波振荡器一样，摆锤的周期 T 几乎与振幅无关，尤其$\theta$是在小于大约 15° 的情况下。即使是简单的摆钟也可以精细调整并保持精确。

注意 T 对 g 的依赖性。如果精确知道摆锤的长度，它实际上可以用来测量重力引起的加速度，如下例所示。

示例$\PageIndex{1}$: Measuring Acceleration due to Gravity by the Period of a Pendulum

在长度为 75.000 cm 的简单摆锤周期为 1.7357 秒的区域中，重力引起的加速度是多少？

策略

给定摆锤的周期 T 和长度 L，我们被要求找出 g。只要假设偏转角小于 15°，我们就可以求解 T = 2$\pi$ L g for g。

解决方案

平方 T = 2$\pi \sqrt{\frac{L}{g}}$ 然后求解 g: $$g = 4\ pi^ {2}\ frac {L} {T^ {2}} ldotp$$
用已知值代入新方程式：$$g = 4\ pi^ {2}\ frac {0.75000\; m} {(1.7357\; s) ^ {2}}\ ldotp$$
计算找出 g: $$g = 9.8281\; m/s^ {2}\ ldotp$$

意义

这种确定 g 的方法可能非常准确，这就是为什么在本示例中将长度和句点指定为五位数的原因。为了$\theta$使近似 sin$\theta$ β 的精度优于摆锤长度和周期的精度，最大位移角应保持在大约 0.5° 以下。

练习$\PageIndex{1}$

工程师建造了两个简单的摆锤。两者都悬挂在固定在房间天花板上的小电线上。每个钟摆在地板上方 2 厘米处徘徊。摆锤1有一个重量为10千克的摆杆。摆锤2有一个重量为100千克的摆杆。描述一下如果两个摆动都移动 12°，摆锤的运动会有何不同。

物理摆锤

任何物体都可以像钟摆一样振荡。考虑将咖啡杯挂在储藏室的挂钩上。如果马克杯被撞了，它会像钟摆一样来回摆动，直到振荡消失。我们将一个简单的钟摆描述为点质量和一根绳子。 物理摆是指振荡与简单摆的振荡相似但不能建模为弦上的点质量的任何物体，质量分布必须包含在运动方程中。

至于简单的摆锤，物理摆的恢复力是重力。使用简单的摆锤，重力作用于摆锤的中心。就物理摆而言，重力作用于物体的质心（CM）。物体围绕一个点 O 摆动。假设一个通用形状的物体，如图所示$\PageIndex{2}$。

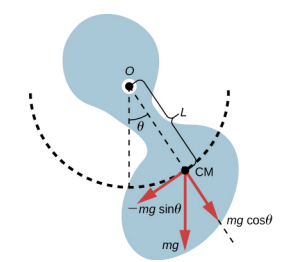
一幅物理钟摆的画。在图中，钟摆是一个形状不规则的物体。质心 C M 是距枢轴点 O 的距离 L。质心描绘了一条以 O 为中心的圆弧。从 O 到 L 的直线从垂直方向逆时针方向成一个 theta 角度。质心处用红色箭头描绘了三种力。力 m g 指向下方。它的分量是减去 m g sine theta，它指向与质心所描绘的弧线相切，以及径向向外指向的 m g cosine theta。 — 图$\PageIndex{2}$：物理摆是指任何像钟摆一样振荡但不能建模为弦上点质量的物体。重力作用在质心 (CM) 上，提供使物体振荡的恢复力。提供恢复力的重量分量上存在负号，因为该力的作用方向与增加角度相反$\theta$。

当物理摆锤悬挂在某个点但可以自由旋转时，它会旋转，因为在 CM 处施加了扭矩，扭矩是由物体重量中与 CM 运动相切的分量产生的。如果逆时针方向为正，则与运动相切的引力分量为 −mg sin$\theta$。负号是恢复力在与增加角度相反的方向上作用的结果。回想一下，扭矩等于$\vec{\tau} = \vec{r} \times \vec{F}$。扭矩的大小等于半径臂的长度乘以施加的力的切向分量，|$\tau$ | = rfsIn$\theta$。在这里，半径臂的长度 L 是旋转点和 CM 之间的距离。要分析运动，请从净扭矩开始。就像简单的钟摆一样，只考虑小角度，这样罪恶就是$\theta$ β$\theta$。回想一下旋转时固定轴旋转时净扭矩等于惯性矩 I =$\int$ r ² dm 乘以角加速度$\alpha$，其中\ (\ alpha =\ frac {d^ {2}\ theta} {d^ {2}}：

\[I \alpha = \tau_{net} = L (-mg) \sin \theta \ldotp\]

使用小角度近似值并重新排列：

\[\begin{split} I \alpha & = -L (mg) \theta; \\ I \frac{d^{2} \theta}{dt^{2}} & = -L (mg) \theta; \\ \frac{d^{2} \theta}{dt^{2}} & = - \left(\dfrac{mgL}{I}\right) \theta \ldotp \end{split}\]

再一次，该方程表示位置的二阶时间导数（在本例中为角度）等于减去一个常数$\left(− \dfrac{mgL}{I}\right)$乘以位置。解决的办法是

\[\theta (t) = \Theta \cos (\omega t + \phi),\]

其中$\Theta$是最大角位移。角频率是

\[\omega = \sqrt{\frac{mgL}{I}} \ldotp \label{15.20}\]

因此，这段时间是

\[T = 2 \pi \sqrt{\frac{I}{mgL}} \ldotp \label{15.21}\]

请注意，对于简单的摆锤，惯性矩为 I =$\int$ r ² dm = mL ²，周期减少为 T = 2$\pi \sqrt{\frac{L}{g}}$。

示例$\PageIndex{2}$: Reducing the Swaying of a Skyscraper

在极端条件下，由于强风或地震活动，摩天大楼最多可以摇摆两米，频率高达20.00 Hz。几家公司开发了放置在摩天大楼顶部的物理摆锤。当摩天大楼向右摆动时，钟摆向左摆动，从而减少摇摆。假设振荡的频率为 0.50 Hz，设计一个由长光束组成、密度恒定、质量为 100 公吨、光束一端有一个枢轴点的摆锤。光束的长度应该是多少？

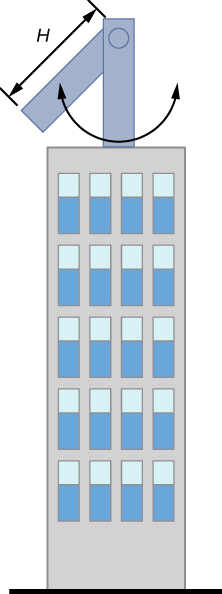
该图描绘了一座高层建筑，其屋顶上有一根柱子，还有一根长度为 H 的长杆，该杆在立柱顶部附近的枢轴点上摆动。

策略

我们被要求找出质量已知的物理摆的长度。我们首先需要找到光束的惯性矩。然后，我们可以使用物理钟摆周期的方程来求出长度。

解决方案

找出 CM 的惯性矩。
使用平行轴定理找出旋转点周围的惯性矩：$$I = I_ {CM} +\ frac {L^ {2}} {4} M =\ frac {1} {12} ML^ {2} +\ frac {1} {2} =\ frac {1} {3} ML^ {2}\ ldotp$$
物理摆的周期为 T = 2$\pi \sqrt{\frac{I}{mgL}}$。使用惯性矩求解长度 L: $$\ begin {split} T & = 2\ pi\ sqrt {\ frac {I} {mgL}} = 2\ pi\ sqrt {\ frac {1} {3} ML^ {2}} = 2\ pi\ sqrt {\ frac {L} {3g}};\\ L & = 3g\ 左 (\ dfrac {T} {2\ pi}\ 右) ^ {2} = 3 (9.8\; m/s^ {2})\ 左 (\ dfrac {2\; s} {2\ pi}\ 右) ^ {2} = 2.98\; m\ ldotp\ end {split} $$
这个长度 L 是从质心到旋转轴的长度，即摆长度的一半。因此，钟摆的长度 H 为：$$ H = 2L = 5.96\: m $$

意义

减少振荡的方法有很多，包括修改摩天大楼的形状、使用多个物理摆和使用调整质量阻尼器。

扭摆

扭摆由由光线或弹簧悬挂的刚性主体组成（图$\PageIndex{3}$）。当身体扭曲一个较小的最大角度 ($\Theta$) 并从静止状态中释放出来时，身体会在 ($\theta$= +$\Theta$) 和 ($\theta$= −$\Theta$) 之间振荡。恢复扭矩由剪切绳索或电线提供。

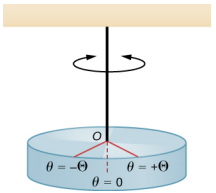
恢复扭矩可以建模为与角度成正比：

\[\tau = - \kappa \theta \ldotp\]

变量 kappa ($\kappa$) 被称为电线或绳子的扭力常数。负号表示恢复扭矩的作用方向与增加角位移的方向相反。净扭矩等于惯性矩乘以角加速度：

\[\begin{split} I \frac{d^{2} \theta}{dt^{2}} & = - \kappa \theta; \\ \frac{d^{2} \theta}{dt^{2}} & = - \frac{\kappa}{I} \theta \ldotp \end{split}\]

这个方程表示位置的二阶时间导数（在本例中为角度）等于负常数乘以位置。这看起来与 SHM$\frac{d^{2} x}{dt^{2}}$ = −$\frac{k}{m}$ x 的运动方程非常相似，其中发现周期为 T = 2$\pi \sqrt{\frac{m}{k}}$。因此，可以使用以下方法找到扭摆周期

\[T = 2 \pi \sqrt{\frac{I}{\kappa}} \ldotp \label{15.22}\]

扭矩常数的单位为 [$\kappa$] = N • m = (kg • m/s ²) m = kg • m ² ^{/s 2}，惯性矩的单位为 [I] = kg • m ²，这表明周期的单位是第二个。

示例$\PageIndex{3}$: Measuring the Torsion Constant of a String

鱼竿的长度为 l = 0.30 m，质量为 4.00 千克。一根绳子固定在杆的 CM 上，系统悬挂在天花板上（图$\PageIndex{4}$）。杆从平衡位置移动 10°，然后从静止状态中松开。棒的振荡周期为 0.5 秒。扭力常数是多$\kappa$少？

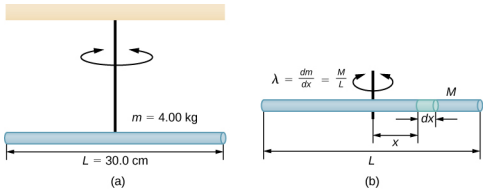
图 a 显示了一根长度为 30.0 厘米、质量为 4.00 千克的水平杆，由一根绳子悬挂在天花板上。绳子附着在杆的中间。杆随着绳子在水平面旋转。图 b 显示了探测杆的惯性矩所需的细节。杆的端到端长度为 L，其总质量为 M。它的线性质量密度 lambda 等于 d m d x，也等于 M over L。突出显示了距离杆中心 x 长度为 d x 的一小部分杆。绳子固定在杆中央的杆上。 — 图$\PageIndex{4}$-(a) 一根用绳子悬挂在天花板上的杆子。 (b) 找出杆的惯性矩。

策略

我们被要求找到弦的扭力常数。我们首先需要找到惯性矩。

解决方案

找出 CM 的惯性矩：$$I_ {CM} =\ int x^ {2} dm =\ int_ {-\ frac {L} {2}} ^ {+\ frac {L} {2}} x^ {2}\ lambda dx =\ lambda\ Bigg [\ frac {x^ {3}} {3}\ Bigg] _ {-\ frac L} {2} ^ {+\ frac {L} {2}} =\ lambda\ frac {2L^ {3}} {24} =\ 左 (\ dfrac {M} {L}\ 右)\ frac {2L^ {3}} {24} =\ frac {1} {12} ML^ {2}\ ldotp$$
使用周期的方程计算扭力常数：$$\ begin {split} T & = 2\ pi\ sqrt {\ frac {I} {\ kappa}}；\\\ kappa & = 我\ 左 (\ dfrac {2\ pi} {T}\ 右) ^ {2}\ 右左 (\ dfrac {2\ pi} {T}\ 右) ^ {2};\\ & =\ Big [\ frac {1} {12} (4.00\; kg) (0.30\; m) ^ {2}\ Big]\左 (\ dfrac {2\ pi} {0.50\; s}\ 右) ^ {2} = 4.73\; N\;\ cdotp m\ ldotp\ end {split} $$

意义

与方块和弹簧系统的力常数一样，扭力常数越大，周期越短。

示例\(\PageIndex{1}\): Measuring Acceleration due to Gravity by the Period of a Pendulum

解决方案

练习\(\PageIndex{1}\)

示例\(\PageIndex{2}\): Reducing the Swaying of a Skyscraper

解决方案

示例\(\PageIndex{3}\): Measuring the Torsion Constant of a String

解决方案