15.4：比较简单谐波运动和圆周运动

Last updated
Save as PDF

Page ID: 205009

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

学习目标

描述正弦和余弦函数与圆周运动概念的关系
描述简单谐波运动和圆周运动之间的联系

对简单谐波运动 (SHM) 进行建模的一种简单方法是考虑均匀的圆周运动。图中\(\PageIndex{1}\)显示了使用此方法的一种方法。钉子（木柱体）固定在垂直圆盘上，以恒定的角频旋转。

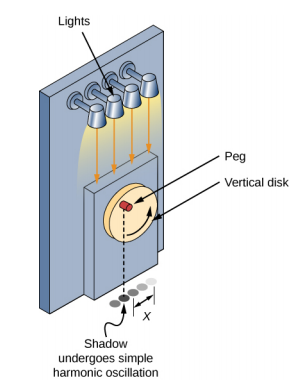
本文中讨论的投射振荡阴影的方法的示意图。钉子从垂直安装在墙壁上的垂直旋转盘上伸出。一组灯光照下来，从上方照亮钉子。钉子的阴影如下所示，如振荡期间多次看到的那样，沿着与墙壁平行的线形成一系列点。从线中心到阴影位置的距离为 x。 — 图\(\PageIndex{1}\)：通过观察以恒定角频率旋转的车轮上的钉子的阴影，可以将 SHM 建模为旋转运动。

该图\(\PageIndex{2}\)显示了磁盘和挂钩的侧视图。如果在圆盘上方放置一盏灯并将其钉住，则钉子会产生阴影。假设圆盘的半径为 r = A，并将与圆盘中心线重合的阴影位置定义为 x = 0.00 m。当圆盘以恒定速率旋转时，阴影在 x = + A 和 x = −A 之间振荡。现在想象一下地板下方弹簧上有一个方块，如图所示\(\PageIndex{2}\)。

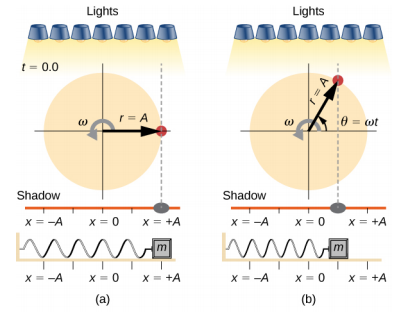
对旋转圆盘上钉子的角度位置、其阴影的位置以及质量在水平弹簧上振荡的位置的比较。在每幅图中，钉子由一组灯光从上方照亮，在水平线上投射阴影。圆盘的半径为 r = A，逆时针旋转，角速度 omega。当钉子直接位于圆盘中心的右侧时，钉子 theta 的角度位置为零。弹簧附着在左边的墙上，右边是团块。质量和阴影的位置为 x，其中 x=0 位于圆盘中心的正下方，x=-a 位于圆盘左边缘的正下方，x=+a 位于圆盘右边缘的正下方。在图 a 中，t=0.0。钉子直接位于圆盘中心的右侧。它的阴影和质量都在 x = +A 处。在图 b 中，在第一象限中，钉子的角度为 theta 等于 omega t。它的阴影和质量都在钉子的正下方，看似是 x = +A/2。未指定时间。在图 c 中，t=t/4。钉子正好位于圆盘中心的正上方。它的角度位置 theta 等于 omega t。它的阴影和质量都在 x =0 处。在图 d 中，钉子的角度为 theta 等于 omega t，现在位于第二象限。它的阴影和质量都在钉子的正下方，看似是 x =-A/2。未指定时间。 — 图\(\PageIndex{2}\)：光线照射到光盘上，这样钉子就会产生阴影。如果圆盘以恰到好处的角频率旋转，则阴影会跟随方块在弹簧上的运动。如果没有能量因非保守势力而消散，那么方块和阴影将齐心协力来回摆动。在此图中，四个快照是在四个不同的时间拍摄的。 (a) 轮子起始于\(\theta\) = 0°，钉子的阴影位于 x = + A 处，表示位置 x = + A 处的质量。(b) 当圆盘旋转角度\(\theta\) =\(\omega\) t 时，钉子的阴影介于 x = + A 和 x = 0 之间。 (c) 圆盘继续旋转直到\(\theta\) = 90°，此时阴影跟随质量变为 x = 0。 (d) 圆盘继续旋转，阴影跟随质量块的位置。

如果圆盘以正确的角频率转动，则阴影会随方块一起出现。阴影的位置可以用方程建模

\[x(t) = A \cos (\omega t) \ldotp \label{15.14}\]

回想一下，附着在弹簧上的方块不会以恒定速度移动。方向盘必须多久转一次才能让钉子的阴影始终出现在方块上？圆盘必须以恒定的角频率转动，该频率等于振荡频率的 2\(\pi\) 倍（\(\omega\)= 2\(\pi\) f）。

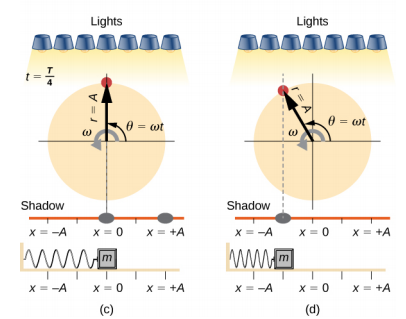
图中\(\PageIndex{3}\)显示了均匀圆周运动与 SHM 之间的基本关系。钉子位于半径的顶端，距圆盘中心 A 的距离。 x 轴由一条平行于地面的直线定义，将圆盘切成两半。 y 轴（未显示）由一条垂直于地面的直线定义，将圆盘切成左半部分和右半部分。圆盘的中心是点（x = 0，y = 0）。将钉子的位置投影到固定的 x 轴上给出了阴影的位置，阴影经历的 SHM 类似于方块和弹簧的系统。在图中所示的时间，投影的位置为 x 并随速度向左移动\(v\)。环绕圆圈的钉子的切向速度等\(\bar{v}_{max}\)于弹簧上的方块。速度的 x 分量等于弹簧上方块的速度。

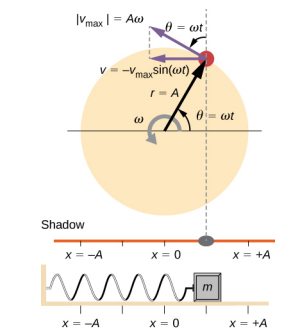
对旋转圆盘上钉子的角度位置、其阴影的位置以及质量在水平弹簧上振荡的位置的比较。圆盘的半径为 r = A，逆时针旋转，角速度 omega。当钉子直接位于圆盘中心的右侧时，钉子 theta 的角度位置为零，在所示时间等于 omega t。钉子的线性速度显示为与圆盘边缘的圆相切的矢量。它的幅度为 v sub max，等于 A 欧米茄。它的 x 分量是一个水平向左向量 — v sub max times sub max 正弦欧米茄 t。钉子在水平线上投射阴影。弹簧附着在左边的墙上，右边是团块。质量和阴影的位置为 x，其中 x=0 位于圆盘中心的正下方，x=-a 位于圆盘左边缘的正下方，x=+a 位于圆盘右边缘的正下方。在图中，钉子位于第一个象限中。它的阴影和质量都在 0 和加 A 之间的 x 位置（在图中似乎在 x = A/2 处）。 — 图\(\PageIndex{3}\)：-以恒定角速度 ω在圆形路径上移动的钉子正在进行均匀的圆周运动。它在 x 轴上的投影经过 SHM。还显示了钉子绕圆的速度 v _max 及其投影，即 v。请注意，这些速度形成了与位移三角形相似的三角形。

我们可以使用图形\(\PageIndex{3}\)来分析圆盘旋转时阴影的速度。钉子围成一圈移动，速度为 v _max = A\(\omega\)。阴影的移动速度等于钉子速度的分量，该分量平行于产生阴影的表面：

\[v = -v_{max} \sin (\omega t) \ldotp \label{15.15}\]

因此，加速度为

\[a = -a_{max} \cos (\omega t) \ldotp \label{15.16}\]

练习 15.3

识别经历均匀圆周运动的物体。描述如何追踪这个物体的 SHM。