15.3：简单谐波运动中的能量

Last updated
Save as PDF

Page ID: 204998

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

学习目标

描述质量和弹簧系统的节能
解释稳定和不稳定平衡点的概念

要在物体中产生变形，我们必须努力。也就是说，无论你是弹吉他弦还是压缩汽车的减震器，都必须通过一定距离施加力。如果唯一的结果是变形，并且没有功率进入热能、声音能或动能，那么所有功率最初都作为某种形式的势能存储在变形物体中。

举一个附着在无摩擦工作台上的弹簧上的方块在 SHM 中振荡的例子。弹簧的力是一种保守力（您在势能和能量守恒一章中对此进行了研究），我们可以为其定义潜在能量。这种势能是弹簧伸展或压缩时储存在弹簧中的能量。在这种情况下，方块在一个维度上振荡，弹簧的力与运动平行作用：

\[W = \int_{x_{i}}^{x_{f}} F_{x} dx \int_{x_{i}}^{x_{f}} -kxdx = \Big[ - \frac{1}{2} kx^{2} \Big]_{x_{i}}^{x_{f}} = - \Big[ \frac{1}{2} kx_{f}^{2} - \frac{1}{2} kx_{i}^{2} \Big] = - [U_{f} - U_{i}] = - \Delta U \ldotp\]

在考虑储存在弹簧中的能量时，标记为 x _i = 0.00 m 的平衡位置是弹簧中存储的能量等于零的位置。当弹簧被拉伸或压缩一个距离 x 时，弹簧中存储的势能为

\[U = \frac{1}{2} kx^{2} \ldotp\]

能量和简单谐波振荡器

要研究简单谐波振荡器的能量，我们需要考虑所有形式的能量。举一个附着在弹簧上的方块放在无摩擦表面上，在 SHM 中振荡的例子。弹簧变形中存储的势能是

\[U = \frac{1}{2} kx^{2} \ldotp\]

在简单的谐波振荡器中，能量在质量 K =\(\frac{1}{2}\) mv ² 的动能和储存在弹簧中的势能 U =\(\frac{1}{2}\) kx ² 之间振荡。在质量和弹簧系统的 SHM 中，没有耗散力，因此总能量是势能和动能的总和。在本节中，我们将考虑系统的能量守恒问题。所研究的概念适用于所有简单的谐波振荡器，包括那些由引力起作用的谐波振荡器。

以图（图）为例\(\PageIndex{1}\)，该图显示了附着在弹簧上的振动块。在无阻尼的 SHM 中，能量在动能和势位之间来回摆动，随着系统的振荡，能量完全从一种形式转移到另一种形式。因此，举一个附着在弹簧上的无摩擦表面上的物体的简单例子，运动从弹簧中存储的所有能量作为弹性势能开始。当物体开始移动时，弹性势能被转化为动能，在平衡位置变成完全的动能。然后，弹簧在拉伸或压缩时将能量转化为弹性势能。当动能完全转换后，速度变为零，然后重复这个循环。了解这些循环中的能量守恒将在此处以及SHM的后续应用（例如交流电路）中提供更多见解。

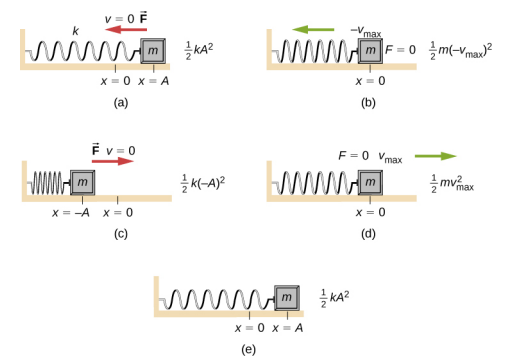
附着在水平弹簧上的质量在其运动的各个点上的运动和能量，弹簧常数 k。在图 (a) 中，质量被移至 x =0 右侧的 x = A 位置，然后从静止状态中释放 (v=0。) 弹簧被拉伸了。质量上的力在左边。该图标有半个 k A 的平方。 (b) 质量在 x = 0 处移动，沿负 x 方向移动，速度 — v sub max。春天很轻松。质量上的力为零。图中标有半个量 v sub max 的平方。 (c) 质量在负 A 处，在 x = 0 的左边，处于静止状态 (v =0。) 弹簧被压缩。力 F 在右边。该图用一半 k 量减去 A 的平方来标记。 (d) 质量在 x = 0 处移动，沿正 x 方向移动，速度加上 v sub max。春天很轻松。质量上的力为零。该图标有半个 m v sub max 的平方。 (e) 质量再次位于 x =0 右侧的 x = A 处。该图标有半个 k A 的平方。 — 图\(\PageIndex{1}\)：在无摩擦表面上附着在弹簧上的物体在 SHM 中的能量转换。 (a) 当质量位于 x = + A 的位置时，所有能量都作为势能存储在弹簧 U =\(\frac{1}{2}\) kA ² 中。动能等于零，因为质量的速度为零。 (b) 当质量向 x = −A 移动时，质量会穿过 x = 0 的位置。此时，弹簧既未延伸也未压缩，因此弹簧中储存的势能为零。在 x = 0 时，总能量均为动能，其中 K =\(\frac{1}{2}\) m（−v _max）²。 (c) 质量继续移动直到到达 x = −A，质量停止并开始向 x = + A 移动。在 x = −A 位置，总能量作为势能存储在压缩的 U =\(\frac{1}{2}\) k (−A) ² 中，动能为零。 (d) 当质量通过 x = 0 位置时，动能为 K =\(\frac{1}{2}\) mv _max ²，弹簧中存储的势能为零。 (e) 质量返回到 x = + A 的位置，其中 K = 0，U =\(\frac{1}{2}\) kA ²。

以图为\(\PageIndex{1}\)例，它显示了周期性运动中特定点的能量。在保持恒定的同时，能量在方块的动能和弹簧中存储的势能之间振荡：

\[E_{Total} = U + K = \frac{1}{2} kx^{2} + \frac{1}{2} mv^{2} \ldotp\]

在 SHM 中，方块在弹簧上的运动由位置 x (t) = Acos\(\omega\) t +\(\phi\)) 定义，速度为 v (t) = −A\(\omega\) sin (\(\omega\)t +\(\phi\))。使用这些方程，三角恒等式 cos ^2\(\theta\) ^{+ sin 2}\(\theta\) = 1\(\omega = \sqrt{\frac{k}{m}}\)，我们可以找到系统的总能量：

\[\begin{split} E_{Total} & = \frac{1}{2} kA^{2} \cos^{2} (\omega t + \phi) + \frac{1}{2} mA^{2} \omega^{2} \sin^{2} (\omega t + \phi) \\ & = \frac{1}{2} kA^{2} \cos^{2} (\omega t + \phi) + \frac{1}{2} mA^{2} \left(\dfrac{k}{m}\right) \sin^{2} (\omega t + \phi) \\ & = \frac{1}{2} kA^{2} \cos^{2} (\omega t + \phi) + \frac{1}{2} kA^{2} \sin^{2} (\omega t + \phi) \\ & = \frac{1}{2} kA^{2} \cos^{2} (\omega t + \phi) + \frac{1}{2} mA^{2} \omega^{2} \sin^{2} (\omega t + \phi) \\ & = \frac{1}{2} kA^{2} (\cos^{2} (\omega t + \phi) + \sin^{2} (\omega t + \phi)) \\ & = \frac{1}{2} kA^{2} \ldotp \end{split}\]

方块和弹簧系统的总能量等于弹簧中存储的势能之和加上方块的动能，并且与振幅 E T _otal =\(\left(\dfrac{1}{2}\right)\) kA ² 的平方成正比。系统的总能量是恒定的。

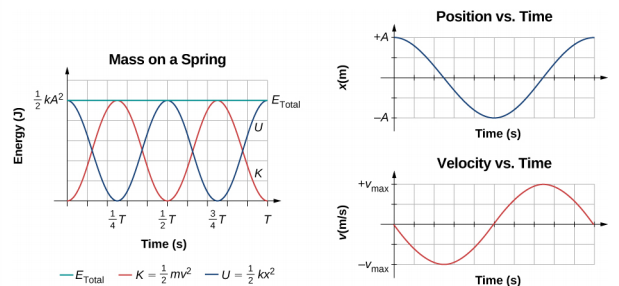
仔细观察系统的能量就会发现，动能像正弦平方函数一样振荡，而势能像余弦平方函数一样振荡。但是，系统的总能量是恒定的，与振幅的平方成正比。该图\(\PageIndex{2}\)显示了方块和弹簧系统的势能、动能和总能量随时间变化的曲线。还绘制了随时间变化的位置和速度。在时间 t = 0.0 秒之前，方块附着在弹簧上并放置在平衡位置。通过施加外力，将其拉到 x = + A 的位置来完成方块的工作。系统现在在弹簧中储存了势能。在时间 t = 0.00 s 时，方块的位置等于振幅，储存在弹簧中的势能等于 U =\(\frac{1}{2}\) kA ²，方块上的力为最大且指向负 x 方向（F _S = −kA）。在时间 t = 0.00 s 时，方块的速度和动能为零。在时间 t = 0.00 s 时，方块从静止状态中释放。

弹簧上质量的能量、位置和速度作为时间函数的图表。左边是以焦耳 (J) 为单位的能量与时间（以秒为单位）的对比图。垂直轴范围为零到一半 k A 的平方。水平轴范围为 0 到 T。显示了三条曲线。总能量 E 子总量显示为绿线。总能量是一个常数，其值为一半 k A 的平方。动能 K 等于一半 m v 的平方，显示为红色曲线。 K 从 t=0 处的零能量开始，在时间 1/4 T 处上升到最大值为一半 k A 的平方，然后在 1/2 T 时减小到零，在 3/4 T 处上升到一半 k A 的平方，在 T 处再次为零。势能 U 等于一半 k x 平方显示为蓝色曲线。 U 起始最大能量为一半 k A 在 t=0 处平方，在 1/4 T 时减至零，在 1/2 T 处上升到一半 k A 的平方，在 3/4 T 时再次为零，在 t=t 时又达到最大值为半 k A 的平方。右边是速度与时间关系图上方的位置与时间的关系图。位置图以 x 为单位，范围从 —A 到 +A，时间单位为秒。位置位于 +A，在 t=0 处减小，达到最小值 —a，然后上升到 +A。速度图以 m/s 为单位为 v，范围从负 v sub max 到加 v sub max 不等，相对于以秒为单位的时间。速度为零，在 t=0 时降低，在位置图为零的同时达到最小值-负 v sub max。当位置处于 x=-a 时，速度再次为零；当位置为零时，速度上升到加 v sub max；在图表末尾 v=0，位置再次为最大值。 — 图\(\PageIndex{2}\)：SHM 中在弹簧上振荡的方块的动能、势能和总能量图。还显示了位置与时间和速度与时间的关系图。总能量保持不变，但能量在动能和势能之间振荡。当动能为最大值时，势能为零。当速度为最大且质量处于平衡位置时，就会发生这种情况。当速度为零时，势能为最大。总能量是动能加上势能之和，它是恒定的。

关于平衡位置的振荡

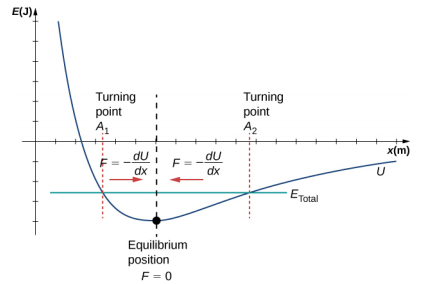
我们刚刚将SHM的能量视为时间的函数。简单谐波振荡器的另一个有趣观点是将能量视为位置的函数。该图\(\PageIndex{3}\)显示了正在进行 SHM 的系统的能量与位置的对比图。

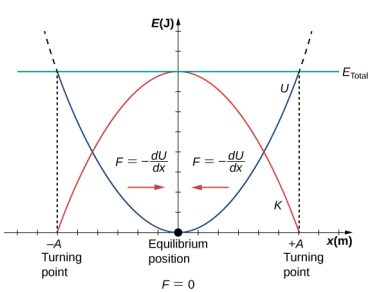
垂直轴上以焦耳为单位的能量 E 与水平轴上的位置 x（以米为单位）的图表。水平轴将 x=0 标记为平衡位置，F=0。位置 x=-a 和 x=+a 被标记为转折点。红色下凹抛物线，标记为 K，在 x=0 处的最大值为 E=E total，在 x=-a 和 x=+a 处为零。E 总和恒定 E 值处的水平绿线被标记为 E 总计。标为 U 的蓝色向上凹抛物线与绿线相交，在 x=-a 和 x=+A 处的总值为 E=E，在 x=0 处为零。 x=0 左侧的图形区域用指向右边的红色箭头标记，方程 F 等于 U 与 x 的导数。x=0 右边的图形区域用指向左边的红色箭头标记，方程 F 等于减去 U 的导数尊重 x。 — 图\(\PageIndex{3}\)：简单谐波振荡器的动能（红色）、势能（蓝色）和总能量（绿色）的图表。力等于 F = −\(\frac{dU}{dx}\)。平衡位置显示为黑点，是力等于零的点。当 x 0 时 < 0, negative when x >，力为正；当 x = 0 时，力等于零。

图中的势能曲线\(\PageIndex{3}\)类似于一个碗。当将大理石放入碗中时，它会沉淀到碗的最低点（x = 0）的平衡位置。之所以发生这种情况，是因为恢复力指向平衡点。这个平衡点有时被称为定点。当大理石受到干扰到不同的位置（x = + A）时，大理石会围绕平衡位置振荡。回顾势能图，通过观察势能图的斜率（F = −\(\frac{dU}{dx}\)）可以找到力。由于定点两侧的力指向平衡点，因此平衡点被称为稳定的平衡点。点 x = A 和 x = −A 被称为转折点。（参见 “潜在能量和节能”。）稳定性是一个重要的概念。如果平衡点是稳定的，则最初处于稳定平衡点的物体受到轻微干扰将导致该物体围绕该点振荡。之所以出现稳定的平衡点，是因为两侧的力都指向它。对于不稳定的平衡点，如果物体受到轻微干扰，它不会返回到平衡点。

以碗中的大理石为例。如果碗向右向上，则大理石如果受到轻微干扰，将在稳定的平衡点周围振荡。如果将碗倒过来，则大理石可以在顶部保持平衡，即净力为零的平衡点。但是，如果大理石受到轻微的干扰，它不会回到平衡点，而是会从碗里滚下来。原因是平衡点两侧的力都偏离该点。这个点是一个不稳定的平衡点。

图中\(\PageIndex{4}\)显示了三个条件。第一个是稳定的平衡点 (a)，第二个是不稳定的平衡点 (b)，最后一个也是不稳定的平衡点 (c)，因为只有一侧的力指向平衡点。

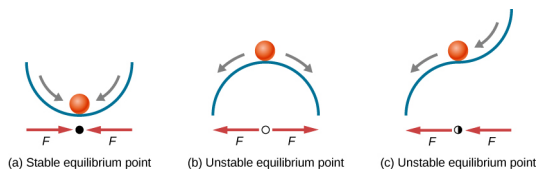
三幅表面球的插图。在图 a 中，稳定的平衡点，球位于凹面内，位于底部。表面下方、球下方的实心圆有两个标记为 F 的水平箭头，从两侧指向该圆圈。与表面相切的灰色箭头显示在表面内部，指向斜坡的下方，指向球的位置。在图 b 中，不稳定的平衡点，球位于凹陷表面的顶部，位于顶部。球表面下方的空圆圈有两个标记为 F 的水平箭头，指向球的两侧。与表面相切的灰色箭头显示在表面内部，指向斜坡的下方，远离球的位置。在图 c 中，不稳定的平衡点，球位于表面的拐点上。表面下方、球下方的半填充圆有两个标记为 F 的水平箭头，一个在圆的两侧，都指向左边。与表面相切的灰色箭头显示在曲面内部，指向斜坡下方，一个指向球，另一个指向远离斜坡。 — 图\(\PageIndex{4}\)：平衡点示例。 (a) 稳定的平衡点；(b) 不稳定的平衡点；(c) 不稳定的平衡点（有时称为半稳定的平衡点）。

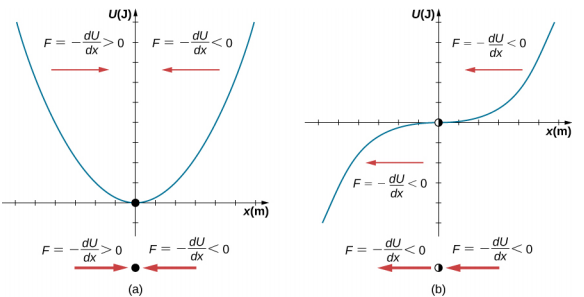
确定平衡点是稳定还是不稳定的过程可以正式化。以图中所示的势能曲线为例\(\PageIndex{5}\)。通过分析图形的斜率可以找到力。力为 F = −\(\frac{dU}{dx}\)。在 (a) 中，定点位于 x = 0.00 m。当 x < 0.00 m 时，力为正。当 x > 0.00 m 时，力为负。这是一个稳定的点。在 (b) 中，定点位于 x = 0.00 m 处。当 x < 0.00 m 时，力为负。当 x > 0.00 m 时，力也为负。这是一个不稳定的问题。

垂直轴上以焦耳为单位的两张 U 图，是水平轴上 x（以米为单位）的函数。在图 a 中，U of x 是一个向上开口的抛物线，其顶点用黑点标记，位于 x=0，U=0。 x=0 左侧的图形区域标有指向右侧的红色箭头，方程 F 等于减去 U 相对于 x 的导数大于零。 x=0 右侧的图形区域用指向左侧的红色箭头标记，方程 F 等于减去 U 相对于 x 的导数小于零。图表下方是红色箭头副本与力关系之间的点的副本，F 等于减去 U 相对于 x 的导数在左侧大于零，F 等于减去 U 相对于 x 的导数在右侧小于零。在图 b 中，U of x 是一个递增函数，其拐点在 x=0 处用半实心圆标记，U=0。 x=0 左侧的图形区域用指向左侧的红色箭头标记，方程 F 等于减去 U 相对于 x 的导数小于零。 x=0 右侧的图形区域也标有指向左侧的红色箭头，方程 F 等于减去 U 相对于 x 的导数小于零。图表下方是红色箭头副本之间的圆的副本，两者均指向左边，而力关系 F 等于减去 U 相对于 x 的导数左侧小于零，F 等于减去 U 相对于 x 的导数在右侧小于零。 — 图\(\PageIndex{5}\)：势能函数的两个示例。某个位置的力等于该位置上图形斜率的负值。 (a) 具有稳定平衡点的势能函数。 (b) 平衡点不稳定的势能函数。这个点有时被称为半稳定点，因为一侧的力指向定点。

稳定平衡点概念的实际应用是分子中两个中性原子之间的力。如果两个分子相距很近，相隔几个原子直径，它们就会感受到一种吸引人的力。如果分子移动得足够近以至于其他电子的电子壳重叠，则分子之间的力就会变得令人反感。两个原子之间的吸引力可能导致原子形成分子。两个分子之间的力不是线性力，不能简单地建模为两个质量被弹簧隔开，但是当从平衡位置偏离少量时，分子的原子可以围绕平衡点振荡。原子由于两个原子之间的吸引力和排斥力而振荡。

以两个原子之间相互作用的一个例子为例，即范德华相互作用。深入讨论两个原子的相互作用超出了本章的范围，但是可以通过考虑系统势能模型的一个例子来研究原子的振荡。对这种分子的势能进行建模的一个建议是使用 Lennard-Jones 6-12 的电位：

\[U(x) = 4 \epsilon \Bigg[ \left(\dfrac{\sigma}{x}\right)^{12} - \left(\dfrac{\sigma}{x}\right)^{6} \Bigg] \ldotp\]

此函数的图表如图所示\(\PageIndex{6}\)。这两个参数\(\epsilon\)和\(\sigma\)是通过实验找到的。

垂直轴上以焦耳为单位的 E 的带注释图表，与水平轴上 x（以米为单位）的函数关系。 Lennard-Jones 势位 U 显示为一条蓝色曲线，在小 x 处为正值。它迅速减小，变为负值，并持续减小，直到在标记为平衡位置 F=0 的位置达到最小值，然后逐渐增加并渐近接近 E=0 但是仍然是负数。一条恒定负值的水平绿线被标记为 E 总计。绿色和蓝色 E 总曲线和 U 曲线在两个位置交叉。平衡位置左侧交叉点的 x 值被标记为转折点减去 A，平衡位置右侧的交叉点被标记为转折点，加 A。平衡位置左侧的图形区域用指向右侧的红色箭头标记方程 F 等于减去 U 相对于的导数。平衡位置右侧的图形区域用指向左侧的红色箭头标记，方程 F 等于 U 相对于 x 的导数。 — 图\(\PageIndex{6}\)：由两个中性原子组成的系统的伦纳德-琼斯势能函数。如果能量低于某个最大能量，则系统会在两个转折点之间的平衡位置附近振荡。

从图中可以看到有一个势能井，它与图中讨论的简单谐波振荡器的势能函数的势能函数的势能井有一些相似之处\(\PageIndex{3}\)。伦纳德-琼斯势具有稳定的平衡点，其中势能最小，平衡点两侧的力都指向平衡点。请注意，与简单的谐波振荡器不同，伦纳德-琼斯电位的电位井不是对称的。这是因为原子之间的力不是胡克定律力，也不是线性的。原子仍然可以在平衡位置 x _min 周围振荡，因为当 x < x _min 时，力为正；当 x > x _min 时，力为负。请注意，当 x 接近零时，斜率相当陡峭且为负，这意味着力很大且为正。这表明尝试将原子推近需要很大的力。随着 x 变得越来越大，斜率变得不那么陡峭，力变小且为负。这表明，如果给定足够大的能量，原子就可以分离。

如果你对这种相互作用感兴趣，可以通过取势能函数的导数来找出分子之间的力。你会立即看到该力与胡克定律力（F = −kx）不相似，但是如果你熟悉二项式定理：

\[(1 + x)^{n} = 1 + nx + \frac{n(n - 1)}{2!} x^{2} + \frac{n(n - 1)(n - 2)}{3!} x^{3} + \cdots,\]

力可以用胡克定律力近似。

速度和节能

回到图中方块和弹簧的系统\(\PageIndex{1}\)，一旦方块从静止状态中释放出来，它就会开始朝负方向向平衡位置移动。势能减小，速度和动能的大小增加。在时间 t = 时\(\frac{T}{4}\)，方块到达平衡位置 x = 0.00 m，方块上的力和势能为零。在平衡位置，方块达到负速度，其幅度等于最大速度 v = −A\(\omega\)。动能为最大值，等于 K =\(\frac{1}{2}\) mv ² = m\(\frac{1}{2}\) A ² Ω\(\omega^{2}\) =\(\frac{1}{2}\) kA ²。此时，方块上的力为零，但动量承载方块，并沿负方向继续朝向 x = −A 方向移动。随着方块继续移动，其上的力朝正方向起作用，速度和动能的大小减小。随着弹簧的压缩，势能增加。在时间 t = 时\(\frac{T}{2}\)，方块到达 x = −A。这里的速度和动能等于零。方块上的力为 F = + kA，弹簧中存储的势能为 U =\(\frac{1}{2}\) kA ²。在振荡期间，总能量是恒定的，等于系统的势能和动能之和，

\[E_{Total} = \frac{1}{2} kx^{2} + \frac{1}{2} mv^{2} = \frac{1}{2} kA^{2} \ldotp \label{15.12}\]

可以求解与 SHM 相关的能量方程以找出任何位置的速度大小：

\[|v| = \sqrt{\frac{k}{m} (A^{2} - x^{2})} \ldotp \label{15.13}\]

简单谐波振荡器中的能量与振幅的平方成正比。在考虑多种形式的振荡时，你会发现能量与振幅的平方成正比。

练习 15.1

即使每个系统的位移相等，如果你用尺子折断手，为什么比用松动的弹簧折断手会更痛苦？

练习 15.2

找出一种方法可以降低简单谐波振荡器的最大速度。