15.2: 简单谐波运动

Last updated
Save as PDF

Page ID: 205020

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

学习目标

定义周期和频率这两个术语
列出简单谐波运动的特征
解释相移的概念
为正在经历简单谐波运动的质量和弹簧系统写下运动方程
描述质量体在垂直弹簧上振荡的运动

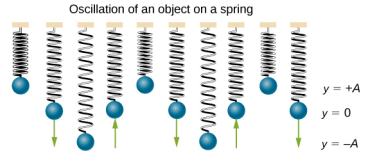
当你弹吉他弦时，生成的声音具有稳定的音调并持续很长时间（图\(\PageIndex{1}\)）。琴弦围绕平衡位置振动，当琴弦从初始位置开始，移动到其中一个极端位置，然后移动到另一个极端位置，然后返回到其初始位置时，一次振荡就完成了。我们将周期性运动定义为任何以固定时间间隔自身重复的动作，例如由吉他弦或儿童在秋千上摆动所表现出的动作。在本节中，我们将研究振荡的基本特征及其数学描述。

一张正在弹吉他的照片。 — 图\(\PageIndex{1}\)：弹奏吉他弦时，琴弦以周期性运动上下振荡。振动弦使周围的空气分子振荡，产生声波。（来源：Tsutaka Tsutano）

振荡周期和频率

在没有摩擦的情况下，完成一次振荡的时间保持不变，称为周期 (T)。它的单位通常是秒，但可以是任何方便的时间单位。 “周期” 一词是指某个事件的时间，无论是否重复，但在本章中，我们将主要讨论周期性运动，顾名思义，周期运动是重复的。

与周期密切相关的概念是事件的频率。 频率 (f) 定义为每单位时间的事件数。对于周期性运动，频率是每单位时间的振荡次数。频率和周期之间的关系是

\[f = \frac{1}{T} \ldotp \label{15.1}\]

频率的 SI 单位是赫兹 (Hz)，定义为每秒一个周期：

\[1\; Hz = 1\; cycle/sec\; or\; 1\; Hz = \frac{1}{s} = 1\; s^{-1} \ldotp\]

一个周期就是一次完整的振荡

示例\(\PageIndex{1}\): Determining the Frequency of Medical Ultrasound

医疗专业人员使用超声波机器制作用于检查人体内脏器官的图像。超声波机器发出高频声波，这些声波会从器官上反射，计算机接收波浪，用它们来创建画面。我们可以根据我们对振荡的了解，使用本模块中提供的公式来确定频率。以医学成像设备为例，它通过振荡产生超声波的周期为0.400\(\mu\) 秒。这种振荡的频率是多少？

策略

给出了周期 (T)，并要求我们找出频率 (f)。

解决方案

用 0.400 µs 代替 f 中的 T =\(\frac{1}{T}\):

\[f = \frac{1}{T} = \frac{1}{0.400 \times 10^{-6}\; s} \ldotp \nonumber\]

求解后找到

\[f = 2.50 \times 10^{6}\; Hz \ldotp \nonumber\]

意义

这种声音频率远高于人类能听到的最高频率（人类听觉范围为 20 Hz 到 20,000 Hz）；因此，它被称为超声波。该频率下的适当振荡会生成用于非侵入性医学诊断的超声波，例如观察子宫内的胎儿。

简单谐波运动的特征

一种非常常见的周期运动称为简单谐波运动 (SHM)。使用 SHM 振荡的系统称为简单的谐波振荡器。

简单谐波运动

在简单的谐波运动中，系统的加速度以及净力与位移成正比，作用方向与位移相反。

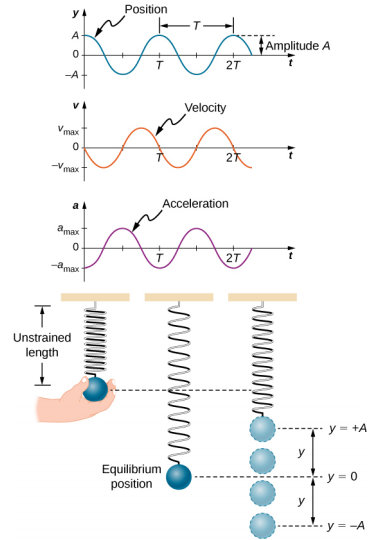
SHM 的一个很好的例子是将质量\(m\)附着在无摩擦表面上的弹簧上的物体，如图所示\(\PageIndex{2}\)。物体围绕平衡位置振荡，物体上的净力等于弹簧提供的力。如前一章所述，这种力量服从胡克定律 F _s = −kx。

如果净力可以用胡克定律来描述并且没有阻尼（由于摩擦或其他非保守力而减速），那么一个简单的谐波振荡器在平衡位置的两侧都会以相等的位移振荡，如图中弹簧上的物体所示\(\PageIndex{2}\)。平衡的最大位移称为振幅 (A)。振幅和位移的单位相同，但取决于振荡的类型。对于弹簧上的物体，振幅和位移的单位是米。

附着在水平弹簧上的质量体（弹簧常数 k）在其运动的各个点的运动和自由体图。在图 (a) 中，质量被移至 x =0 右侧的 x = A 位置，然后从静止状态中释放 (v=0。) 弹簧被拉伸了。质量上的力在左边。自由体图的权重 w 向下，法向力 N 向上等于重量，力 F 向左。 (b) 质量在 x = 0 处移动，沿负 x 方向移动，速度 — v sub max。春天很轻松。质量上的力为零。自由体图的重量 w 向下，法向力 N 向上，等于重量。 (c) 质量在负 A 处，在 x = 0 的左边，处于静止状态 (v =0。) 弹簧被压缩。力 F 在右边。自由体图的权重 w 向下，法向力 N 向上等于重量，力 F 向右。 (d) 质量在 x = 0 处移动，沿正 x 方向移动，速度加上 v sub max。春天很轻松。质量上的力为零。自由体图的重量 w 向下，法向力 N 向上，等于重量。 (e) 质量再次位于 x =0 右侧的 x = A 处，然后处于静止状态 (v=0。) 弹簧被拉伸了。质量上的力在左边。自由体图的权重 w 向下，法向力 N 向上等于重量，力 F 向左。 — 图\(\PageIndex{2}\)：-附着在无摩擦表面上滑动的弹簧上的物体是一个简单的简单谐波振荡器。在上面的一组图中，质量物体附着在弹簧上并放在无摩擦的桌子上。弹簧的另一端固定在墙上。当弹簧既未拉伸也未压缩时，质量的位置标记为 x = 0，是平衡位置。 (a) 肿块移至 x = A 位置并从静止状态中释放。 (b) 质量在负 x 方向上移动时会加速，在 x = 0 时达到最大负速度。 (c) 质量继续向负 x 方向移动，减速直到 x = −A 处停止。 (d) 质量现在开始向正 x 方向加速，在 x = 0 时达到正最大速度。 (e) 然后，质量继续向正方向移动，直到 x = A 处停止。质量在 SHM 中延续，振幅为 A，周期为 T。物体的最大速度发生在它通过平衡时。弹簧越硬，周期 T 越小。物体的质量越大，周期 T 越大。

SHM 有何重要意义？首先，简单谐波振荡器的周期\(T\)和频率\(f\)与振幅无关。例如，无论是轻弹还是用力弹吉他的琴弦都会以相同的频率振荡。

两个重要因素确实会影响简单谐波振荡器的周期。这段时间与系统的僵硬程度有关。非常坚硬的物体具有较大的力常数 (k)，这会使系统的周期变短。例如，你可以调整跳水板的刚度——它越硬，振动越快，周期越短。周期还取决于振荡系统的质量。系统规模越大，时间越长。例如，跳水板上的沉重人物上下弹跳的速度比轻的人慢。实际上，质量 m 和力常数 k 是影响 SHM 周期和频率的唯一因素。要得出周期和频率的方程，我们必须首先定义和分析运动方程。请注意，力常数有时被称为弹簧常数。

SHM 的方程

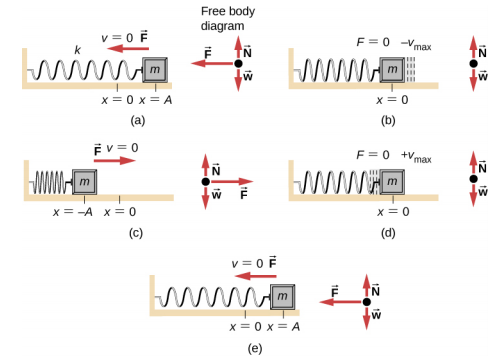
假设在无摩擦工作台上的弹簧上安装了一个方块（图\(\PageIndex{3}\)）。平衡位置（弹簧既未拉伸也未压缩的位置）标记为 x = 0。在平衡位置，净力为零。

方块固定在水平弹簧上并放置在无摩擦的桌子上。平衡位置，即弹簧既未伸展也未压缩，标记为 x=0。方块左侧的位置标记为 x =-A，距离方块右侧相同距离的位置标记为 x = + A。 — 图\(\PageIndex{3}\)：一个方块固定在弹簧上，放在无摩擦的桌子上。平衡位置，即弹簧既未伸展也未压缩，标记为 x = 0。

在方块上完成工作，将其拉到 x = + A 的位置，然后将其从静止状态中释放。最大 x 位置 (A) 称为运动振幅。方块开始在 SHM 中在 x = + A 和 x = −A 之间振荡，其中 A 是运动的振幅，T 是振荡周期。周期是指一次振荡的时间。图中\(\PageIndex{4}\)显示了方块在释放后完成一次半振荡时的运动。

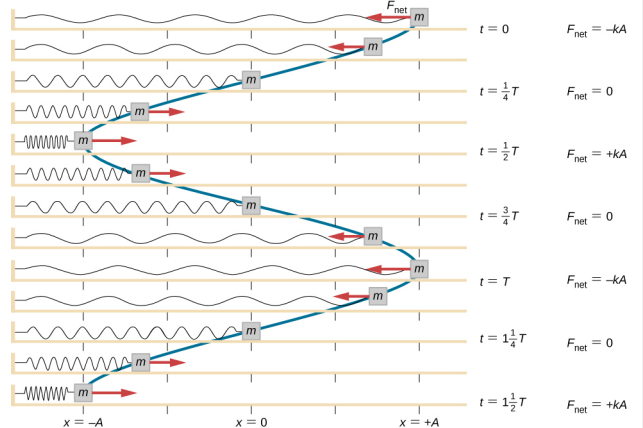
图中显示了附着在水平弹簧上并在水平表面上滑动的质量的一系列插图。质量的位置、弹簧和对质量的力每八个周期显示一次，从 t = 0 到 t = 一个半周期。插图垂直对齐，质量的位置使用蓝线从一个图形连接到另一个图形，从而创建了位置（水平）依赖于时间（垂直）的图形。 x = 0 的位置位于水平表面的中心。在上图中，质量为 x = +A，净力在左边，等于 — k A。弹簧的拉伸量最大。时间为 t = 0。在第二张图中，质量介于 x = +A/2 和 x = A 之间，净力在左边，小于上一张图中的值。弹簧的拉伸程度小于 t=0 时的拉伸量。在第三张图中，质量为 x = 0，没有净力。春天很轻松。时间为 t = 四分之一 T 在第四张图中，质量介于 x =-A/2 和 x =-A 之间，净力在右边。力的大小与第二张图中的力的大小相同。弹簧有些压缩。在第五张图中，质量在 x =-A 处，净力在右边，等于 + k A。弹簧的压缩量最大。时间为 t = 1/2 T 在第六张图中，质量介于 x =-A/2 和 x =-A 之间，净力在右边。力的大小与第二张图中的力的大小相同。弹簧有些压缩。这张图与第四张图相同。在第七张图中，质量为 x = 0，没有净力。春天很轻松。时间为 t = 3/4 T。此图形与第三张图相同。在第八张图中，质量介于 x = +A/2 和 x = A 之间，净力在左边。这张图与第二张图相同。在第九张图中，质量为 x = +A，净力在左边，等于 — k A。弹簧的拉伸量最大。时间为 t = 0。此图表与第一个（顶部）图表相同。其余四张图重复第二、第三、第四和第五张图，第十一张图的时间为 t = 1 和 1/4 T，第十三张图的时间为 t = 1 和 1/2 T。连接质量位置的曲线形成垂直正弦曲线。 — 图\(\PageIndex{4}\)：一个方块固定在弹簧的一端，放在无摩擦的桌子上。弹簧的另一端固定在墙上。净力等于零的平衡位置被标记为 x = 0 m。在方块上完成工作，将其拉出 x = + A，方块从静止状态中释放。方块在 x = + A 和 x = −A 之间振荡。力也显示为矢量。

该图\(\PageIndex{4}\)显示了区块位置随时间变化的曲线。当绘制位置随时间变化时，很明显，数据可以通过具有振幅\(A\)和周期的余弦函数进行建模\(T\)。余弦函数 cos 每隔 2 的倍数\(\theta\)重复一次\(\pi\)，而方块的运动每一个周期 T 重复一次。但是，该函数\(\cos \left(\dfrac{2 \pi}{T} t \right)\)重复周期的每一个整数倍数。余弦函数的最大值为一，因此必须将余弦函数乘以振幅 A。

\[x(t) = A \cos \left(\dfrac{2 \pi}{T} t \right) = A \cos (\omega t) \ldotp \label{15.2}\]

回想一下关于旋转的章节，角频率等于\(\omega = \frac{d \theta}{dt}\)。在这种情况下，周期是恒定的，因此角频率定义为 2\(\pi\) 除以周期\(\omega = \frac{2 \pi}{T}\)。

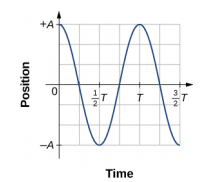
垂直轴上的位置随时间变化而在水平轴上的图表。垂直比例为 From — A 到 +A，水平比例从 0 到 3/2 T。曲线是一个余弦函数，时间为 0 时的值为 +A，时间 T 处的值又为 +A — 图\(\PageIndex{5}\)：图中所示方块位置\(\PageIndex{4}\)随时间变化的图表。位置可以建模为周期函数，例如余弦函数或正弦函数。

将位置作为时间函数的方程\(x(t) = A\cos( \omega t)\)适用于建模数据，其中模块在初始时间 t = 0.00 s 的位置位于振幅 A 处，初始速度为零。在获取实验数据时，质量在初始时间 t = 0.00 s 的位置通常不等于振幅，初始速度也不为零。以学生在实验室中收集的 10 秒数据为例，如图所示\(\PageIndex{6}\)。

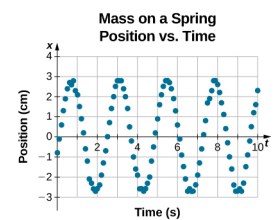
弹簧上质量块的位置与时间对比数据。水平轴是时间 t（以秒为单位），范围从 0 到 10 秒。垂直轴以厘米为单位的 x 位置，范围从 -3 厘米到 4 厘米不等。数据显示为点，似乎以每秒大约 10 点的速度定期获取。数据呈正弦波动，在显示的 10 秒数据中，整个周期略高于四个完整周期。 t=0 处的位置为 x = -0.8 厘米。该位置的最大值为 x = 3 厘米，大约 t = 0.6 秒、3.1 秒、5.5 秒和 7.9 秒。在大约 t=1.9 秒、4.3 秒、6.7 秒和 9.0 秒时，位置最小为 x = -3 厘米。 — 图\(\PageIndex{6}\)：学生在实验室收集的数据显示了使用声波测距仪测量的弹簧块的位置。数据是从时间 t = 0.00 开始收集的，但初始位置在位置 x β − 0.80 cm ≤ 3.00 cm 附近，因此初始位置不等于振幅 x ₀ = + A。速度是位置的时间导数，即位置随时间变化图表上某点的斜率。在时间 t = 0.00 s 时，速度不是 v = 0.00 m/s，位置与时间对比图的斜率就证明了这一点，该斜率在初始时间不为零。

图中的数据仍然\(\PageIndex{6}\)可以使用周期函数（如余弦函数）建模，但函数向右移动。这种转变被称为相移，通常用希腊字母 phi (\(\phi\)) 表示。弹簧上方块的位置随时间变化的方程变成

\[x(t) = A \cos (\omega t + \phi) \ldotp\]

这是 SHM 的广义方程，其中 t 是以秒为单位测量的时间，\(\omega\)是以反秒为单位的角频率，A 是以米或厘米为单位测量的振幅，\(\phi\)是以弧度为单位测量的相移（图\(\PageIndex{7}\)）。应该注意的是，由于正弦函数和余弦函数的差异仅在于相移，因此可以使用余弦或正弦函数对这个运动进行建模。

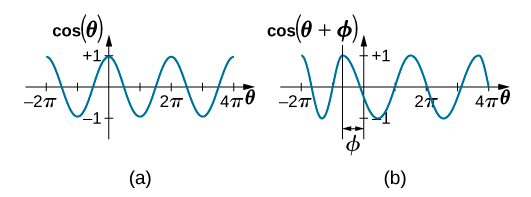
两张角度振荡函数的图表。在图 a 中，我们将函数 theta 的余弦看作是 theta 的函数，从负 pi 到二 pi。该函数在 -1 和 +1 之间振荡，在 theta 等于零时的最大值为 +1。在图 b 中，我们将数量 theta plus phi 的余弦函数看作是 theta 的函数，从负 pi 到二 pi。该函数在 -1 和 +1 之间振荡，在 theta 等于 phi 时的最大值。曲线是余弦曲线，向右移动一定量 phi。 — 图\(\PageIndex{7}\)：(a) 余弦函数。 (b) 余弦函数向右移动一个角度\(\phi\)。该角度\(\phi\)被称为函数的相移。

弹簧上质量在 SHM 中振荡的速度可以通过取位置方程的导数得出：

\[v(t) = \frac{dx}{dt} = \frac{d}{dt} (A \cos (\omega t + \phi)) = -A \omega \sin(\omega t + \varphi) = -v_{max} \sin (\omega t + \phi) \ldotp\]

由于正弦函数在 —1 和 +1 之间振荡，因此最大速度是振幅乘以角频率，v _max = A\(\omega\)。当质量向 x = + A 移动时，最大速度出现在平衡位置 (x = 0)，当质量向 x = −A 移动时，负方向的最大速度是在平衡位置 (x = 0) 达到的，等于 −v _ma x。

弹簧上质量的加速度可以通过取速度的时间导数得出：

\[a(t) = \frac{dv}{dt} = \frac{d}{dt} (-A \omega \sin (\omega t + \phi)) = -A \omega^{2} \cos (\omega t + \varphi) = -a_{max} \cos (\omega t + \phi) \ldotp\]

最大加速度为 a _max = A\(\omega^{2}\)。最大加速度出现在位置 (x = −A)，加速度出现在位置 (x = −A)，等于 −a _max。

SHM 运动方程摘要

总而言之，弹簧上方块的振荡运动可以使用以下运动方程进行建模：

\[ \begin{align} x(t) &= A \cos (\omega t + \phi) \label{15.3} \\[4pt] v(t) &= -v_{max} \sin (\omega t + \phi) \label{15.4} \\[4pt] a(t) &= -a_{max} \cos (\omega t + \phi) \label{15.5} \end{align}\]

和

\[ \begin{align} x_{max} &= A \label{15.6} \\[4pt] v_{max} &= A \omega \label{15.7} \\[4pt] a_{max} &= A \omega^{2} \ldotp \label{15.8} \end{align}\]

这里\(A\)是运动的振幅，\(T\)是周期，\(\phi\)是相移，\(\omega = \frac{2 \pi}{T}\)= 2\(\pi\) f 是方块运动的角频率。

示例 15.2：确定方块和弹簧的运动方程

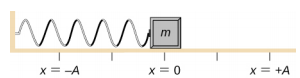
在无摩擦的表面上放置一个 2.00 千克的方块。力常数为 k = 32.00 N/m 的弹簧连接到方块上，弹簧的另一端连接到墙上。弹簧可以压缩或延伸。平衡位置标记为 x = 0.00 m。在方块上完成工作，将其拉出 x = + 0.02 m。方块从静止状态中释放出来，在 x = + 0.02 m 和 x = −0.02 m 之间振荡。运动周期为 1.57 秒。确定运动方程。

策略

我们首先找到角频率。相移为零，\(\phi\)= 0.00 rad，因为方块在 x = A = + 0.02 m 处从静止状态中释放。一旦找到角频率，我们就可以确定最大速度和最大加速度。

解决方案

可以找到角频率并将其用于查找最大速度和最大加速度：

\[\begin{split} \omega & = \frac{2 \pi}{1.57\; s} = 4.00\; s^{-1}; \\ v_{max} & = A \omega = (0.02\; m)(4.00\; s^{-1}) = 0.08\; m/s; \\ a_{max} & = A \omega^{2} = (0.02; m)(4.00\; s^{-1})^{2} = 0.32\; m/s^{2} \ldotp \end{split}\]

剩下的就是填写运动方程式：

\[\begin{split} x(t) & = a \cos (\omega t + \phi) = (0.02\; m) \cos (4.00\; s^{-1} t); \\ v(t) & = -v_{max} \sin (\omega t + \phi) = (-0.8\; m/s) \sin (4.00\; s^{-1} t); \\ a(t) & = -a_{max} \cos (\omega t + \phi) = (-0.32\; m/s^{2}) \cos (4.00\; s^{-1} t) \ldotp \end{split}\]

意义

可以随时找到位置、速度和加速度。请务必记住，在使用这些方程时，您的计算器必须处于弧度模式。

弹簧上弥撒的周期和频率

附着在弹簧上的物体的 SHM 的一个有趣特征是，角频率以及运动的周期和频率仅取决于质量和力常数，而不取决于其他因素，例如运动的振幅。我们可以使用运动方程和牛顿第二定律 (\(\vec{F}_{net} = m \vec{a}\)) 来找到角频率、频率和周期的方程。

以无摩擦表面上的弹簧上的方块为例。质量上有三种力：重量、法向力和弹簧产生的力。仅有的两种垂直于表面起作用的力是重量和法向力，它们的幅度相等，方向相反，因此总和为零。与表面平行起作用的唯一力是弹簧产生的力，因此净力必须等于弹簧的力：

\[\begin{split} F_{x} & = -kx; \\ ma & = -kx; \\ m \frac{d^{2} x}{dt^{2}} & = -kx; \\ \frac{d^{2} x}{dt^{2}} & = - \frac{k}{m} x \ldotp \end{split}\]

用运动方程代替 x 和 a 可以得到

\[-A \omega^{2} \cos (\omega t + \phi) = - \frac{k}{m} A \cos (\omega t +\phi) \ldotp\]

取消类似的项并求解角频率会产生

\[\omega = \sqrt{\frac{k}{m}} \ldotp \label{15.9}\]

角频率仅取决于力常数和质量，而不取决于振幅。角频率定义为\(\omega = \frac{2 \pi}{T}\)，这会生成运动周期的方程：

\[T = 2 \pi \sqrt{\frac{m}{k}} \ldotp \label{15.10}\]

周期也仅取决于质量和力常数。质量越大，周期越长。弹簧越硬，周期越短。频率是

\[f = \frac{1}{T} = \frac{1}{2 \pi} \sqrt{\frac{k}{m}} \ldotp \label{15.11}\]

垂直运动和水平弹簧

当弹簧垂直悬挂并连接方块并启动时，方块会在 SHM 中振荡。在这种情况下，没有法向力，重力的净效果是改变平衡位置。以图为例\(\PageIndex{8}\)。两种力作用在方块上：弹簧的重量和力。重量是恒定的，弹簧的力会随着弹簧长度的变化而变化。

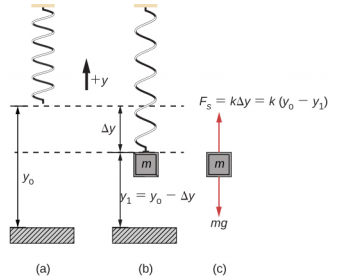
安装在天花板上的垂直弹簧的插图。正 y 方向是向上。在左边的图 a 中，弹簧上没有附着任何质量。弹簧的底部是距离地板零以下的距离。在中间的图 b 中，弹簧的质量为 m。弹簧的顶部与图 a 中的水平相同，但弹簧向下延伸了一段距离 delta y，因此弹簧的底部现在是距地板的 y sub 1 等于 y sub zero 减去 delta y 的距离。右边的图 c 显示了质量的自由体图，向下的力 m g 和向上的力 F sub s 等于 k delta y，也等于 k delta y 的 k 乘以量 y sub 1 减去 y sub 1。 — 图\(\PageIndex{8}\)：弹簧悬挂在天花板上。当方块附着时，方块处于平衡位置，方块的重量等于弹簧的力。 (a) 弹簧悬挂在天花板上，平衡位置标记为 yo。 (b) 当弹簧提供的力等于质量的重量时，质量附着在弹簧上并达到新的平衡位置（\(\Delta\)y ₁ = y ₀ − y）。 (c) 质量的自由体图显示了作用于质量的两种力：重量和弹簧的力。

当方块到达平衡位置时，如图所示\(\PageIndex{8}\)，弹簧的力等于方块的重量，F _net = F _s − mg = 0，其中

\[-k (- \Delta y) = mg \ldotp\]

从图中可以看出，位置的变化是\( \Delta y = y_{0}-y_{1} \)，从那以后\(-k (- \Delta y) = mg\)，我们有

\[k (y_{0} - y_{1}) - mg = 0 \ldotp\]

如果方块被移位并被释放，它将围绕新的平衡位置振荡。如图所示\(\PageIndex{9}\)，如果将方块的位置记录为时间函数，则记录为周期性函数。如果方块移至 y 位置，则净力变为 F _net = k (y ₀-y) − mg。但是我们发现，在平衡位置，mg = k\(\Delta\) y = ky ₀ − ky ₁。用方程中的权重代替得到

\[F_{net} =ky_{0} - ky - (ky_{0} - ky_{1}) = k (y_{1} - y) \ldotp\]

回想一下，y ₁ 只是平衡位置，任何位置都可以设置为点 y = 0.00 m。因此，让我们将 y ₁ 设置为 y = 0.00 m。然后净力变为

\[\begin{split}F_{net} & = -ky; \\ m \frac{d^{2} y}{dt^{2}} & = -ky \ldotp \end{split}\]

这正是我们之前发现的弹簧上水平滑动质量的情况。恒定的重力只能用来改变质量的平衡位置。因此，解的形式应与水平弹簧上的方块相同，y (t) = Acos (\(\omega\)t +\(\phi\))。速度和加速度方程的形式也与水平情况的方程相同。请注意，包含相移意味着实际上可以使用余弦函数或正弦函数对运动进行建模，因为这两个函数的区别仅在于相移。

展示了一系列 10 幅附着在垂直弹簧上的球的插图。插图彼此相邻显示，弹簧顶部对齐。右侧标记了垂直位置 y = + A、y = 0 和 y =-A。从左向右移动：在最左边的图中，弹簧被压缩，所以球处于 y = + A 处静止状态。在第二张图中，球在 y = 0 处向下移动。在第三幅画中，弹簧被拉伸，使球处于 y =-A 处并处于静止状态。在第四张图中，球在 y = 0 处向上移动。在第五张图中，弹簧被压缩，因此球在 y = + A 处处于静止状态。在第六张图中，球在 y = 0 处向下移动。在第七幅画中，弹簧被拉伸，使球处于 y =-A 处并处于静止状态。在第八张图中，球在 y = 0 处向上移动。在第九张图中，弹簧被压缩，因此球在 y = + A 处处于静止状态。在第十张图中，球在 y = 0 处向下移动。这些插图下方是一系列垂直对齐的图表。顶部图表的位置随时间的变化而变化。垂直轴位于 y 位置，范围为 — A 到 +A。水平轴是时间 t，以 T 为增量标记。该图在 t=0 处的值为 y=+a，振荡两个和四分之一周期。最大值之间的水平距离标记为 T，水平轴和最大值之间的垂直距离标记为振幅 A。中间的图表是速度随时间变化的函数。垂直轴是速度 v，范围为负 v sub max 到 v max。水平轴是时间 t，以 T 为增量标记。该图的值为 v=0，在 t=0 处为负斜率，振荡两个和一个四分之一周期。底部图表是加速度随时间变化的函数。垂直轴是加速度 a，范围为减去子最大值到最大值。水平轴是时间 t，以 T 为增量标记。图形的值 a 等于减去子最大值和 a，振荡两个和一个四分之一周期。图表下方是弹簧上球的三幅插图。位置 y = + A、y=0 和 y =-A 在右侧标记。在最左边的图中，一只手握住球，弹簧的长度被标记为无应变长度。此位置高于 y = + A 位置。在中间的图片中，球没有被握住，位于标记为平衡位置的较低位置。此位置为 y = 0。在最右边的图中，球显示在四个不同的位置。这些位置是 y = + A，刚好在 y = 0 上方，刚好低于 y = 0，在 y =-A 处。仅显示弹簧底部在 y = + A 位置与球相连的情况。 — 图\(\PageIndex{9}\)：物体在垂直弹簧上运动的 y (t)、v (t) 和 a (t) 与 t 的对比图。物体上的净力可以用胡克定律来描述，因此物体会经历 SHM。请注意，初始位置的垂直位移为最大值 A；v 最初为零，然后在物体向下移动时为负；初始加速度为负，回到平衡位置并在该点变为零。