12.E:静态平衡和弹性(练习)
- Page ID
- 204802
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)
概念性问题
12.1 静态平衡的条件
- 关于处于动态平衡状态的运动物体的速度,你能说些什么?
- 旋转体在什么条件下可以保持平衡? 举个例子。
- 哪三个因素会影响力相对于特定枢轴点产生的扭矩?
- 机械师在尝试拆下非常紧的螺栓时,有时会在扳手的手柄上放一根长度的管道。 这有什么帮助? 对于接下来的四个问题,请将陈述评估为对还是错,然后解释你的答案。
- 如果只有一种外力(或扭矩)作用于物体,则该物体无法处于平衡状态。
- 如果物体处于平衡状态,则作用在其上的力必须为偶数。
- 如果奇数力的作用在物体上,则该物体无法处于平衡状态。
- 以恒定速度绕圈移动的物体处于旋转平衡状态。
- 钢丝漫步者携带的长而灵活的杆子有什么用途?
12.2 静态平衡示例
- 当地板没有摩擦时,可以将梯子靠在粗糙的墙壁上吗?
- 展示如何使用弹簧秤和简单支点对重量大于体重秤上最大读数的物体进行称重。
- 一位画家爬上梯子。 当画家靠近底部或靠近顶部时,梯子更有可能滑动吗?
12.3 应力、应变和弹性模量
注意:除非另有说明,否则假定电线、棒材和其他元件的重量可以忽略不计。 表 12.1 给出了所选材料的弹性模量。
- 为什么松鼠能从树枝上跳到地上然后完好无损地逃跑,而人类却可以在这样的跌倒中折断骨头?
- 当装满醋的玻璃瓶变热时,醋和玻璃杯都会膨胀,但是醋随着温度的变化而膨胀的幅度比玻璃杯要大得多。 如果瓶子装满到非常紧的瓶盖,瓶子就会破裂。 解释为什么醋上方有一袋空气可以防止瓶子破裂,以及如何防止瓶子破裂。
- 在墙上的两颗钉子之间串起一根细线用来支撑一幅大图。 如果电线被紧紧地串起来,或者如果它被串起来以致下垂得很厉害,它是否会断裂?
- 查看应力和应变之间的关系。 你能发现这两个数量有什么相似之处吗?
- 当你按下木棒的末端时,你在施加什么类型的压力? 你什么时候拉到它的尽头?
- 可以对橡皮筋施加压缩应力吗?
- 杨氏模量可以有负值吗? 那么体积模量呢?
- 如果假设材料的体积模量为负,那么当你挤压其中的一块时会发生什么?
- 讨论如何测量液体的体积模量。
12.4 弹性和可塑性
注意:除非另有说明,否则假定电线、棒材和其他元件的重量可以忽略不计。 表 12.1 给出了所选材料的弹性模量。
- 当钓鱼线被指定为 “10 磅测试” 时,这意味着什么?
- 钢棒通常在凝固之前放置在混凝土中。 这些棒的目的是什么?
问题
12.1 静态平衡的条件
- 拧紧螺栓时,在距离螺栓中心 0.140 m 的距离处,以 165 N 的力垂直推动扳手。 相对于螺栓的中心,你施加了多少扭矩?
- 打开门时,在距离铰链 0.850 m 的距离处,以 55.0 N 的力垂直推动门。 相对于铰链,你施加的扭矩是多少?
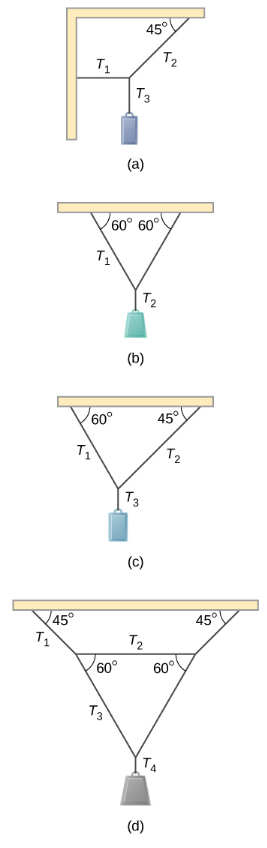
- 找出如下所示的每根支撑电缆的张力大小。 在每种情况下,悬挂体的重量均为100.0 N,电缆的质量可以忽略不计。
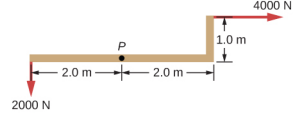
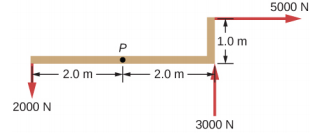
- 必须在 P 点施加什么力才能保持结构的平衡? 该结构的重量可以忽略不计。
- 是否有可能在 P 处施加力以保持所示结构的平衡? 该结构的重量可以忽略不计。
- 两个孩子在玩耍时推门的对面。 两者都水平推动,垂直于门。 一个孩子在距离铰链 0.600 米的距离处以 17.5 N 的力推动,第二个孩子在 0.450 米的距离处推动。第二个孩子必须施加什么力量才能阻止门移动? 假设摩擦力可以忽略不计。
- 一辆重达 1000 公斤的小型 SUV 的轴距为 3.0 m。如果其重量落在前轮上 60%,则货车的质心在前轮后面有多远?
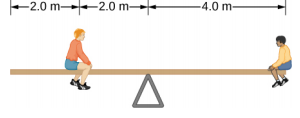
- 统一的跷跷板在其质心处是平衡的,如下所示。 右边那个小男孩的体重为40.0 kg。 他朋友的质量是多少?
12.2 静态平衡示例
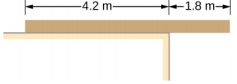
- 一块均匀的木板停留在水平表面上,如下所示。 木板的重量为 30 千克,长 6.0 米。 在它倾斜之前,它的右端可以放置多少质量? (提示:当电路板即将翻倒时,它只能沿着成为瞬间旋转轴的边缘与表面接触。)
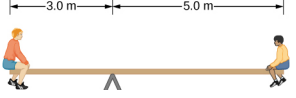
- 下图所示的统一跷跷板在距离左端 3.0 米的支点上保持平衡。 右边的小男孩的体重为40千克,左边的大男孩的体重为80千克。 董事会的质量是多少?
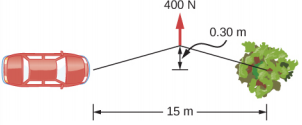
- 为了让他的汽车摆脱泥巴,一个人将绳子的一端绑在前保险杠上,另一端绑在15米外的一棵树上,如下所示。 然后,他用 400 N 的力拉动绳索的中心,这会导致绳子的中心移动 0.30 m,如图所示。 绳子在汽车上的力量是多少?
- 长度为 6.0 m 的 40.0 kg 统一脚手架由两根轻型电缆支撑,如下所示。 一个 80.0 公斤的画家站在脚手架左端 1.0 米处,他的绘画设备距离右端 1.5 米。 如果左侧电缆的张力是右侧电缆的两倍,请找出电缆中的张力和设备的质量。
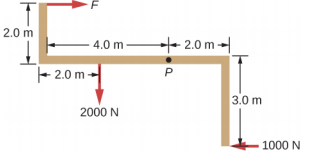
- 当下图所示的结构在 P 点受到支撑时,它处于平衡状态。 找出力 F 的大小和在 P 处施加的力。结构的重量可以忽略不计。
- 为了爬上屋顶,一个人(质量为70.0 kg)在混凝土垫板上放一个6.00米的铝制梯子(质量为10.0 kg),梯子底部距离房屋 2.00 米。 梯子靠在塑料雨槽上,我们可以假设它没有摩擦。 梯子的质心距离底部 2.00 m。 该人站在距离底部 3.00 米处。 在梯子底部找到正常的反作用力和摩擦力。
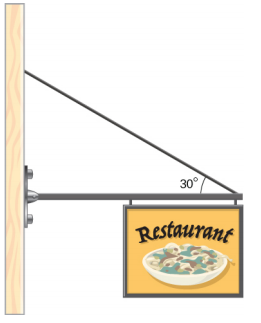
- 统一的水平支柱重 400.0 N。支柱的一端固定在墙上的铰链支撑上,支柱的另一端固定在重 200.0 N 的标志上。支柱还由连接在支柱末端和墙壁之间的电缆支撑。 假设标志的全部重量都附在支柱的最末端,请找出电缆中的张力和支柱铰链处的力。
- 下图所示的前臂\(\theta\)相对于上臂成一定角度,手中握有5.0千克的重量。 前臂和手的总质量为 3.0 kg,它们的质心距离肘部 15.0 cm。 (a) 二头肌在前臂上施加的力是多少\(\theta\) = 60°? (b) 相同角度下肘关节受到的力大小是多少? (c) 这些力如何取决于角度\(\theta\)?
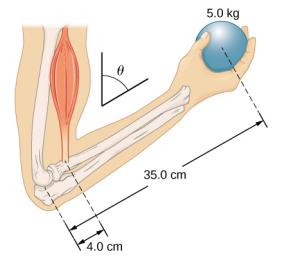
- 下图所示的均匀吊杆重 3000 N。它由水平支撑线和 A 点的铰链支撑支撑支撑,电线和 A 处的支撑对吊杆施加了什么力? A 处的力量会沿着繁荣起作用吗?
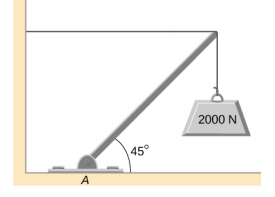
- 下图所示的均匀吊杆重 700 N,悬挂在其右端的物体重 400 N。吊杆由轻型电缆和墙上的铰链支撑。 计算电缆中的张力和吊杆上铰链上的力。 铰链上的力是否沿着吊杆起作用?
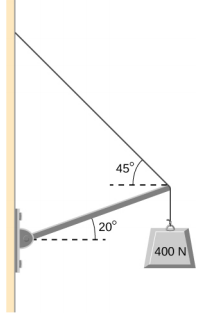
- 起重量为 3000 千克的起重机的 12.0 米吊杆 AB 如下所示。 动臂的质心位于其几何中心,动臂的质量为 1000 kg。 对于所示位置,计算电缆中的张力 T 和轴 A 处的力
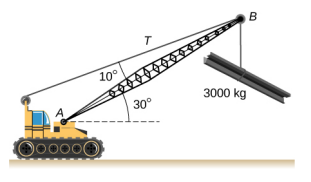
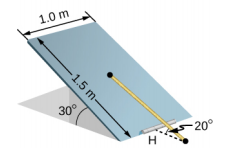
- 下图所示的统一活板门为 1.0 m x 1.5 m,重 300 N。它由单个铰链(H)和绑在门中间和地板之间的轻绳支撑。 门保持在所示位置,其板与水平地板成30°角,绳索与地板成20°角。 找出绳索中的张力和铰链处的力。
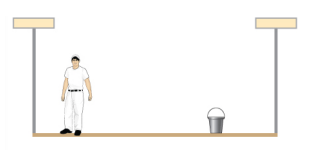
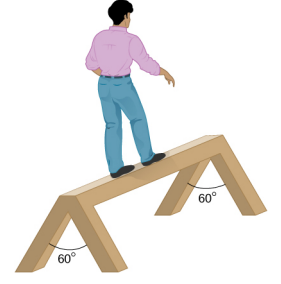
- 一个90公斤的男子在锯马上行走,如下所示。 锯马长 2.0 米,高 1.0 米,质量为 25.0 千克。 计算当人距离锯马远端 0.5 米时,每条腿在与地板接触点上的法向反作用力。 (提示:在两端,先找到总反作用力。 该反作用力是两种反作用力的矢量和,每种反作用力沿一条腿起作用。 与地板接触点处的法向反作用力是该力的法向(相对于地板)分量。)
12.3 应力、应变和弹性模量
- 铅笔中的 “铅” 是一种石墨成分,杨氏模量约为 1.0 x 10 9 N/m 2。 计算在自动铅笔中以 4.0 N 的力直接敲击铅笔中铅笔长度的变化。铅笔直径为 0.50 mm,长 60 mm。
- 电视广播天线是地球上最高的人造结构。 1987 年,一位重达 72.0 公斤的物理学家将自己和 400 千克的设备置于 610 米高的天线的顶部,用于进行重力实验。 如果我们认为天线相当于半径为0.150 m的钢制圆柱体,则压缩了多少?
- 当一个65.0公斤的登山者悬挂在岩石露头下方35.0米时,她直径为0.800厘米的尼龙绳能伸出多少钱? (对于尼龙,Y = 1.35 x 10 9 Pa。)
- 当水冻结时,其体积增加9.05%。 当容器冻结时,每单位面积的水能对容器施加什么力?
- 一位制作葡萄汁的农民将玻璃瓶装到边缘,然后盖紧盖住。 果汁变热时比玻璃杯膨胀得更多,因此体积增加0.2%。 假设瓶子没有破裂,计算果汁每平方厘米施加的力,如果果汁的体积模量为 1.8 x 10 9 N /m 2。
- 脊柱中椎骨之间的圆盘受到 600.0 N 的剪切力,使用 1.0 x 10 9 N/m 2 的剪切模量计算其剪切变形。 圆盘相当于一个高 0.700 厘米、直径 4.00 厘米的实心圆柱体。
- 椎骨承受的剪切力为 500.0 N。找到剪切变形,将椎骨设为高 3.00 厘米、直径 4.00 厘米的圆柱体。 你的结果与前面问题中获得的结果相比如何? 脊柱问题在椎间盘中比在椎骨中更常见吗?
- 如果钢琴钢丝最初长度为 1.35 m 且直径为 0.850 mm,则计算钢琴调谐器在钢琴钢丝拉伸 8.00 mm 时施加的力。
- 20.0 米高的空心铝制旗杆的强度相当于直径为 4.00 cm 的实心圆柱体。 强风使极点弯曲的程度与顶部的水平900.0-N力一样大。 杆的顶部向侧面弯曲多远?
- 当使用直径为 1.0 cm 的铜线以 2.0 m/s 2 的加速度向上提升负载时,它会延伸 1.0%。 负载的重量是多少?
- 在钻探油井时,每段新的钻杆都会承受其自身的重量以及管道和钻头下方的钻头的重量。 计算一根长达 6.00 米的新钢管的伸长度,该钢管支撑一个 100 千克的钻头和 3.00 千米长的管道,线性质量密度为 20.0 kg/m。将管道视为直径为 5.00 cm 的实心圆柱体。
- 密度\(\rho\)为 7.8 g/cm 3 的大型均匀圆柱形钢棒长 2.0 米,直径为 5.0 厘米。 杆固定在混凝土地板上,其长轴垂直。 杆在距其下端 (a) 1.0 m 处的横截面处的法向应力是多少? (b) 距离下端 1.5 米?
- 一名 90 公斤的登山者悬挂在尼龙绳上,将其拉伸 25.0 厘米。 如果绳子最初长 30.0 米,直径为 1.0 厘米,那么尼龙的杨氏模量是多少?
- 悬索桥的吊杆长 25.0 m。 如果拉杆是用钢制成的,那么它的直径必须是多少,这样当一辆2.5 x 10 4 千克的卡车经过时,它的伸展力不会超过 1.0 厘米? 假设拉杆支撑了卡车的所有重量。
- 铜线长 1.0 米,直径为 1.0 毫米。 如果电线垂直悬挂,则必须在其自由端增加多少重量才能将其拉伸 3.0 毫米?
- 悬挂在天花板上的金属线的自由端附着一个 100-N 的重量。 当在电线上添加第二个 100N 重量时,它会延伸 3.0 mm。 电线的直径和长度分别为 1.0 mm 和 2.0 m。 用于制造电线的金属的杨氏模量是多少?
- 材料的体积模量为 1.0 x 10 11 N/m 2。 当这种材料承受 10 7 N/m 2 的体积应力增加时,其体积会发生多少分数变化? 假设力均匀地施加在表面上。
- 大小为 1.0 x 10 6 N 的法向力均匀地施加到封闭一定体积液体的球形表面上。 这会导致表面半径从 50.000 厘米减小到 49.995 厘米。 液体的体积模量是多少?
- 在绳索上行走时,走钢丝的人在两根相距 15.0 米的支撑杆之间拉伸的电线中产生 3.94 x 10 3 N 的张力。 未拉伸时,电线的直径为 0.50 cm。 当助行器在两极之间中间的电线上时,电线会比水平线低5.0°的角度。 当助行器处于这个位置时,这种张力会使钢丝拉伸多少?
- 使用铅笔橡皮擦时,在距离硬木橡皮擦接头 2.00 cm 的距离处施加 6.00 N 的垂直力。 铅笔的直径为 6.00 mm,与水平方向成了 20.0° 的角度。 (a) 木材垂直于其长度弯曲多少? (b) 纵向压缩了多少?
- 法向力均匀地施加在半径为 20.0 cm 的球形体积水的表面上。 如果表面的压力增加了 200 MPa,球体的半径会减少多少?
12.4 弹性和可塑性
- 当其中的拉应力达到 6.00 x 10 6 N/m 2 时,横截面积为 0.50 cm 2 的均匀绳索会断裂。 (a) 用绳索以恒定速度缓慢提升的最大负荷是多少? (b) 在加速度为 4.00 m/s 2 的情况下,绳索可以举起的最大载荷是多少?
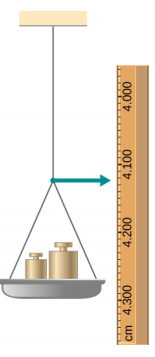
- 长度为 2.0 m、直径 1.0 mm 的垂直金属线的一端连接到天花板上,另一端连接到 5.0N 配重盘上,如下所示。 指针在平底锅前的位置为 4.000 厘米。 然后将不同的权重添加到平移区域,并将指针的位置记录在所示的表格中。 绘制该导线的应力与应变图,然后使用生成的曲线确定杨氏模量和金属的比例极限。 这最有可能是哪种金属?
| 增加负荷(包括平底锅)(N) | 刻度读数 (cm) |
|---|---|
| 0 | 4.000 |
| 15 | 4.036 |
| 25 | 4.073 |
| 35 | 4.109 |
| 45 | 4.146 |
| 55 | 4.181 |
| 65 | 4.221 |
| 75 | 4.266 |
| 85 | 4.316 |
- 一根铝线(\(\rho\)= 2.7 g/cm 3)悬挂在天花板上并垂直悬挂。 电线上端的应力达到比例极限(8.0 x 10 7 N/m 2)之前必须经过多长时间?
其他问题
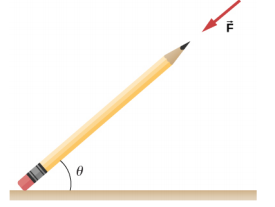
- 铅笔的橡皮擦和桌面之间的静摩擦系数为\(\mu_{s}\) = 0.80。 如果力\(\vec{F}\)是沿着铅笔的轴线施加的,如下所示,那么铅笔在不滑动的情况下可以站立的最小角度是多少? 忽略铅笔的重量。
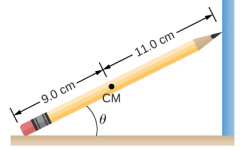
- 铅笔靠在角落上,如下所示。 铅笔的锐化末端碰到光滑的垂直表面,橡皮擦的一端碰到了粗糙的水平地板。 橡皮擦和地板之间的静摩擦系数为\(\mu_{s}\) = 0.80。 铅笔的质心距离橡皮擦尖端 9.0 厘米,距离铅笔芯尖端 11.0 厘米。 找出铅笔不会滑动的最小角度 β。
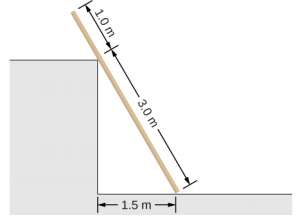
- 一块重 200.0 N 的 4.0 米均匀木板靠在墙角上,如下所示。 木板与角落交汇处没有摩擦力。 (a) 找出角落和地板对木板施加的力。 (b) 为了防止木板滑动,地板和木板之间的最小静摩擦系数是多少?
- 一个 40 公斤的男孩从 3.0 米的高度跳下,用一只脚着陆,撞到地面后在 0.10 秒内休息。 假设他在持续减速的情况下休息。 如果他腿部刚好位于脚踝上方的骨头的总横截面积为 3.0 cm 2,那么这些骨头的压缩应力是多少? 当腿部骨骼承受的压力大于 1.7 x 10 8 Pa 时,它们可能会骨折。 这个男孩有摔断腿的危险吗?
- 两根细棒,一根由钢制成,另一根由铝制成,端到端连接。 每根鱼竿长 2.0 米,横截面积为 9.1 mm 2。 如果在组合的两端施加了 10,000 N 的拉力,请查找:(a) 每根杆中的应力;(b) 每根杆的应变;以及 (c) 每根杆的伸长率。
- 两根棒,一根由铜制成,另一根由钢制成,尺寸相同。 如果铜棒在一定应力下拉伸0.15 mm,那么在同样的应力下钢棒会拉伸多少?
挑战问题
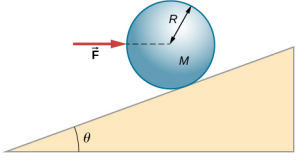
- 水平力\(\vec{F}\)在精确朝向球体中心的方向上施加水平力,如下所示。 找出该力的大小,使球体保持静态平衡。 斜面在球体上的摩擦力是多少?
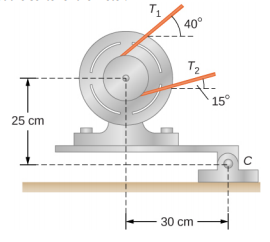
- 当电机安装在旋转支架上时,其重量可用于保持传动皮带的张力。 当电机不运行时,张力 T 1 和 T 2 相等。 平台和电机的总质量为 100.0 kg,传动皮带轮的直径为 16.0 cm。当电机关闭时,找到:(a) 皮带中的张力,以及 (b) 铰链平台支撑处的力 C 点假设马达加平台的质心位于马达。
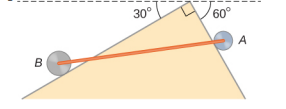
- 两个重量分别为 w 和 2w 的轮子 A 和 B 由一根重量为 w/2 的均匀杆连接,如下所示。 车轮可以在倾斜的表面上自由滚动。 确定系统处于平衡状态时杆与水平线形成的角度。 提示:有五种作用在杆上,即车轮的两个重量,车轮与楔子接触处的两种法向反作用力,以及杆的重量。
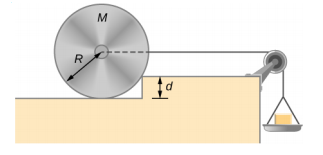
- 权重会逐渐添加到平底锅中,直到质量为 M 和半径为 R 的轮子被拉过高度为 d 的障碍物,如下所示。 完成此任务所需的重量加上平底锅的最小质量是多少?
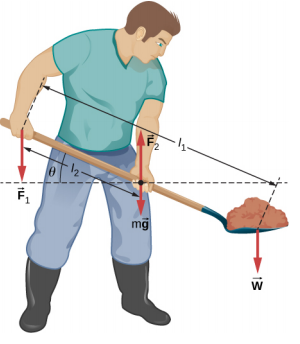
- 为了抬起一铲泥土,园丁在铲子的末端向下推,然后在距离末端 l 2 的距离向上拉,如下所示。 铲子的重量为m\(\vec{g}\),在施加时起作用\(\vec{F}_{2}\)。 计算力\(\vec{F}_{1}\)的大小,以 l 1、l 2、mg 和载荷的重量 W 为函数。\(\vec{F}_{2}\) 为什么你的答案不取决于铲子与水平方向的角度\(theta\)?
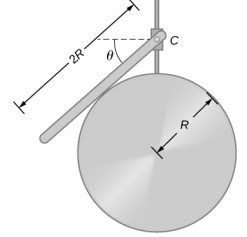
- 长度为 2R 且质量为 M 的均匀杆附着在小套圈 C 上,位于半径为 R 的圆柱形表面上,如下所示。 如果套圈可以沿垂直导轨无摩擦地滑动,请找\(\theta\)出杆处于静态平衡状态的角度。
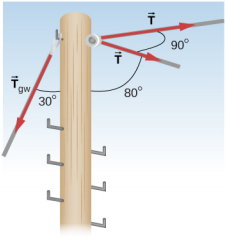
- 下图所示的极点在电力线中处于90.0°的弯曲处,因此比线路直线部分的极点承受的剪切力更大。 按照所示角度,每条线的张力为 4.00 x 10 4 N。 这根杆高 15.0 米,直径为 18.0 厘米,强度可以说是硬木的一半。 (a) 计算极点的压缩率。 (b) 找出它的弯曲程度和方向。 (c) 如果杆子与垂直方向成30.0°的角度连接到杆的顶部,则找出用来保持杆直的电线中的张力。 那根电线与弯道的方向相反。