12.6：弹性和可塑性

Last updated
Save as PDF

Page ID: 204770

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

学习目标

解释材料变形具有弹性的极限
描述材料显示塑性行为的范围
在应力-应变图上分析弹性和塑性

我们将应力和应变之间的比例常数称为弹性模量。但是我们为什么要这样称呼呢？物体具有弹性意味着什么？我们如何描述它的行为？

弹性是指固体物体和材料在消除导致变形的外力（载荷）后恢复其原始形状的趋势。当负载不再存在时，当物体恢复到其原始大小和形状时，它具有弹性。弹性行为的物理原因因材料而异，取决于材料的微观结构。例如，聚合物和橡胶的弹性是由在施加的力下拉伸聚合物链引起的。相比之下，金属的弹性是由在外部施加力的作用下调整晶格（金属的材料结构）的晶体细胞的大小和重塑引起的。

决定材料弹性的两个参数是其弹性模量和弹性极限。对于难以变形的材料，通常使用高弹性模量；换句话说，需要高载荷才能产生显著应变的材料。一个例子是钢带。低弹性模量通常适用于在载荷下容易变形的材料，例如橡皮筋。如果载荷下的应力变得过高，则当载荷被移除时，材料不再恢复到其原始形状和大小，而是松弛到不同的形状和大小：材料会永久变形。 弹性极限是应力值，超过该值后，材料不再具有弹性行为，而是永久变形。

我们对弹性材料的感知既取决于其弹性极限，也取决于其弹性模量。例如，所有橡胶都具有低弹性模量和高弹性极限的特征；因此，它们很容易拉伸，而且弹性明显很大。在具有相同弹性极限的材料中，弹性最强的是弹性模量最低的材料。

当载荷从零增加时，产生的应力与公式 12.4.4 给出的应变成正比，但前提是应力不超过某个极限值。对于线性极限内的应力值，我们可以用类似于弹簧胡克定律来描述弹性行为。根据胡克定律，弹簧在施加力下的拉伸值与力的大小成正比。相反，从弹簧到施加的拉伸的响应力与拉伸成正比。同样，材料在载荷下的变形与载荷成正比，相反，产生的应力与应变成正比。线性极限（或比例极限）是最大的应力值，超过该值的应力将不再与应变成正比。超出线性极限，应力和应变之间的关系不再是线性的。当应力大于线性极限但仍处于弹性极限之内时，行为仍然是弹性的，但应力和应变之间的关系变为非线性。

对于超出弹性极限的应力，材料表现出塑性特性。这意味着材料会不可逆转地变形，即使负载被移除，也不会恢复到其原始形状和大小。当应力逐渐增加到超过弹性极限时，材料会发生塑性变形。橡胶状材料随着应变的增加而显示出应力的增加，这意味着它们变得更难拉伸，最终会到达断裂点并断裂。延性材料（例如金属）显示出随着应变的增加而逐渐减小的应力，这意味着随着应力应变值接近断点，它们变得更容易变形。对于不同的材料，造成材料可塑性的微观机制是不同的。

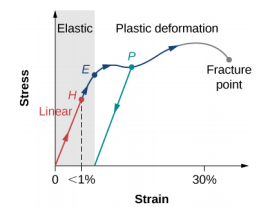
我们可以在应力 -应变图上绘制应力和应变之间的关系。每种材料都有自己的特性应变-应力曲线。负载下延性金属的典型应力应变图如图所示\(\PageIndex{1}\)。在此图中，应变是分数伸长率（未按比例绘制）。当载荷逐渐增加时，从空载点（原点）开始的线性行为（红线）在 H 点的线性极限处结束。如果载荷进一步增加，则应力-应变关系是非线性的，但仍具有弹性。在图中，可以看到点H和E之间的非线性区域。越大的载荷将应力带到弹性极限E，弹性行为在此结束，塑性变形开始。超出弹性极限后，当载荷被移除时，例如在 P 处，材料会沿着绿线松弛到新的形状和大小。也就是说，当应力为零时，材料会永久变形并且不会恢复到其初始形状和大小。

当载荷大到足以使应力超过 E 处的弹性极限时，材料会经历塑性变形。材料会继续发生塑性变形，直到应力到达断裂点（断裂点）。除了断裂点之外，我们不再有材料样本，因此图表在断裂点结束。为了完整地描述这个定性描述，应该说线性、弹性和塑性极限表示了一系列值，而不是一个尖点。

该图显示了应力应变图。当应变低于 1%（点 H）时，应力呈线性增长。塑性变形（标记为 P）发生在 1% 到 30% 之间。应变的进一步增加会导致骨折。 — 图\(\PageIndex{1}\)：负载下金属的典型应力应变图：图表在断裂点结束。箭头显示了在不断增加的载荷下变化的方向。点 H 和 E 分别是线性极限和弹性极限。在 H 点和 E 点之间，行为是非线性的。源于 P 的绿线说明了移除负载时金属的响应。永久变形在绿线与水平轴相交处具有应变值。

断裂点的应力值称为断裂应力（或极限应力）。具有相似弹性特性的材料，例如两种金属，可能具有非常不同的断裂应力。例如，铝的极限应力为 2.2 x 10 ⁸ Pa，钢的极限应力可能高达 20.0 x 10 ⁸ Pa，具体取决于钢的种类。我们可以根据公式 12.4.5 快速估计，对于横截面积为 1 英寸 ² 的棒，铝棒的断裂载荷为 3.2 x 10 ⁴ 磅，而钢棒的断裂载荷大约大九倍。