12.5: 应力、应变和弹性模量(第 2 部分)
- Page ID
- 204820
体积应力、应变和模量
当你潜入水中时,你会感觉到一股力量从各个方向压在身体的每个部位。 那时你所经历的是体积压力,换句话说,压力。 体积应力总是会减小被淹没物体表面所包围的体积。 这种 “挤压” 的力量始终垂直于水下表面 Figure\(\PageIndex{1}\)。 这些力的作用是在没有体积应力的情况下,将水下物体的体积减小一量 V,而物体的体积 V 0。\(\Delta\) 这种变形称为体积应变,通过体积相对于原始体积的变化来描述:
\[bulk\; strain = \frac{\Delta V}{V_{0}} \label{12.37}\]
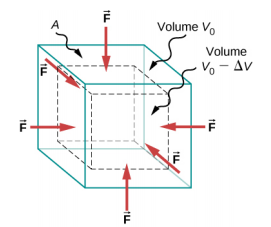
体积应变由体应力产生,体应力是\(\perp\)垂直于表面的力 F,它压在水下物体的单位表面积 A 上。 这种物理量或压力 p 被定义为
\[pressure = p \equiv \frac{F_{\perp}}{A} \ldotp \label{12.38}\]
我们将在流体力学中更详细地研究流体中的压力。 压力的一个重要特征是它是一个标量,没有任何特定的方向;也就是说,压力在所有可能的方向上作用相同。 当你将手浸入水中时,你会感觉到作用于手顶表面的压力与底部表面、侧面或手指之间皮肤表面的压力相同。 在这种情况下,你感觉到的压力比你习惯的手没有浸入水中时的感受要增加\(\Delta\) p。 当你的手没有浸入水中时,你会感觉到一个大气层的正常压力 p 0,它可以作为参考点。 体积应力是压力的增加,即\(\Delta\) p,超过正常水平 p 0。
根据方程 12.4.4,当体应力增加时,体积应变随响应而增加。 这种关系中的比例常数称为体积模量 B 或
\[B = \frac{bulk\; stress}{bulk\; strain} = \frac{\Delta p}{\frac{\Delta V}{V_{0}}} = - \Delta p \frac{V_{0}}{\Delta V} \ldotp \label{12.39}\]
方程式\ ref {12.39} 中出现的减号是为了保持一致性,以确保\(B\)其为正量。 请注意,负号 (—) 是必要的,因为压力\(\Delta\) p 的增加(正量)总是会导致音量降低\(\Delta\) V,而体积的减少是负量。 体积模量的倒数称为压缩率 k,或
\[k = \frac{1}{B} = - \frac{\frac{\Delta V}{V_{0}}}{\Delta p} \ldotp \label{12.40}\]
“可压缩性” 一词用于指流体(气体和液体)。 压缩性描述了每单位压力增加时流体体积的变化。 以大可压缩性为特征的流体相对容易压缩。 例如,水的可压缩性为 4.64 x 10 −5 /atm,丙酮的可压缩性为 1.45 x 10 −4 /atm。 这意味着,在压力升高1.0-atm的情况下,丙酮体积的相对减小幅度大约是水的三倍。
在液压机图中\(\PageIndex{2}\),250升体积的机油会承受2300psi的压力增加。 如果油的可压缩性为 2.0 x 10 −5/atm,则找出压机运行时体积应变和油量的绝对减小值。
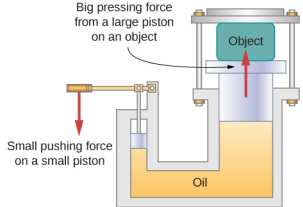
策略
我们必须反转方程\ ref {12.40} 才能找到体积应变。 首先,我们将压力增加从 psi 转换为 atm,\(\Delta\)p = 2300 psi = β\(\frac{2300}{14.7\; atm}\) 160 atm,然后确定 V 0 = 250 L
解决方案
将值代入方程中,我们有
\[bulk\; strain = \frac{\Delta V}{V_{0}} = \frac{\Delta p}{B} = k \Delta p = (2.0 \times 10^{-5}\; /atm)(160\; atm) = 0.0032\]
回答
\[\Delta V = 0.0032 V_{0} = 0.0032 (250\; L) = 0.78\; L \ldotp\]
意义
请注意,由于水的可压缩性是机油的2.32倍,因此如果将该问题的液压机中的工作物质改为水,则体积应变和体积变化将大2.32倍。
如果作用于立方体 1.0 m 3 钢件每个表面的法向力变化了 1.0 x 10 7 N,则找出由此产生的钢块体积变化。
剪切应力、应变和模量
剪应力和应变的概念仅涉及固体物体或材料。 建筑物和构造板块就是可能受到剪切应力的物体的例子。 通常,这些概念不适用于流体。
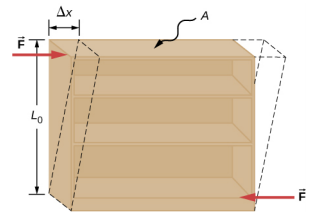
当两个相等大小的反平行力切向固体物体的相对表面施加时,就会发生剪切变形,从而导致力线的横向变形,如图所示的剪切应力的典型示例\(\PageIndex{3}\)。 剪切变形的特征是层在与作用力相切的方向上逐渐移动\(\Delta\) x 层。 \(\Delta\)x 中的这种渐变发生在横向方向上沿一定距离 L 0。 剪切应变由最大位移\(\Delta\) x 与横向距离 L 0 之比来定义
\[shear\; strain = \frac{\Delta x}{L_{0}} \ldotp \label{12.41}\]
剪切应力是由剪切应力引起的。 剪应力是由平行于表面的力引起的。 我们使用符号 F \(\parallel\)表示这些部队。 施加剪切力的\(\parallel\)每个表面积 A 的大小 F 是剪切应力的度量
\[shear\; stress = \frac{F_{\parallel}}{A} \ldotp \label{12.42}\]
剪切模量是方程\ ref {12.33} 中的比例常数,由应力与应变之比定义。 剪切模量通常表示为\(S\):
\[S = \frac{shear\; stress}{shear\; strain} = \frac{\frac{F_{\parallel}}{A}}{\frac{\Delta x}{L_{0}}} = \frac{F_{\parallel}}{A} \frac{L_{0}}{\Delta x} \ldotp \label{12.43}\]
清洁人员试图通过切线推动最顶层书架的表面,在铺有地毯的地板上移动一个沉重的旧书柜。 但是,这种努力的唯一明显效果与图中看到的效果相似\(\PageIndex{2}\),当人停止推动时,它就会消失。 书柜高 180.0 厘米,宽 90.0 厘米,有四个 30.0 厘米深的书架,全部装满了部分书籍。 书柜和书的总重量为 600.0 N。如果该人向顶层书架推动 50.0N,使顶层书架相对于一动不动的底层架子水平移动 15.0 厘米,请找到书柜的剪切模量。
策略
唯一的相关信息是书柜的物理尺寸、切向力的值以及该力造成的位移。 我们确定 F \(\parallel\)= 50.0 N,\(\Delta\)x = 15.0 cm,L 0 = 180.0 cm,A =(30.0 cm)(90.0 cm)= 2700.0 cm 2,我们使用方程\ ref {12.43} 来计算剪切模量。
解决方案
将数字代入方程中,我们得出剪切模量
\[S = \frac{F_{\parallel}}{A} \frac{L_{0}}{\Delta x} = \frac{50.0\; N}{2700.0\; cm^{2}} \frac{180.0\; cm}{15.0\; cm} = \frac{2}{9} \frac{M}{cm^{2}} = \frac{2}{9} \times 10^{4}\; N/m^{2} = \frac{20}{9} \times 10^{3}\; Pa = 2.222\; kPa \ldotp \nonumber\]
我们还可以分别找到剪切应力和应变:
\[\frac{F_{\parallel}}{A} = \frac{50.0\; N}{2700.0\; cm^{2}} = \frac{5}{27}\; kPa = 185.2\; Pa \nonumber\]
\[\frac{\Delta x}{L_{0}} = \frac{15.0\; cm}{180.0\; cm} = \frac{1}{12} = 0.083 \ldotp \nonumber\]
意义
如果这个例子中的人给架子一个健康的推力,那么诱发的剪切可能会把它倒成一堆垃圾。 大致相同的剪切机制是造成填土大坝和堤坝失效的原因;总的来说,滑坡也是造成滑坡的原因。
解释为什么杨氏模量和剪切模量的概念不适用于流体。


