12.4:应力、应变和弹性模量(第 1 部分)
- Page ID
- 204786
- 在描述材料的弹性变形时解释应力和应变的概念
- 描述物体和材料的弹性变形类型
刚体模型是物体在外力作用下不会变形的理想示例。 它在分析机械系统时非常有用,而且许多物理物体的确在很大程度上是刚性的。 物体在多大程度上可以被视为刚性取决于制造该物体的材料的物理特性。 例如,塑料制成的乒乓球很脆弱,而橡胶制成的网球在受到压制力作用时具有弹性。 但是,在其他情况下,乒乓球和网球都可能像刚体一样弹得很好。 同样,设计假肢的人可以通过将人体肢体建模为刚体来近似其力学;但是,骨骼和组织的实际组合是一种弹性介质。
在本节的其余部分中,我们将从考虑影响物体运动的力转向影响物体形状的力。 由于施加力而导致的形状变化被称为变形。 众所周知,即使是非常小的力也会造成一些变形。 物体或物理介质在外部力量的作用下会发生变形,例如,这可能是挤压、挤压、撕裂、扭曲、剪切或拉开物体。 在物理学语言中,有两个术语描述了正在变形的物体上的力:应力和应变。
应力是一个描述导致变形的力大小的量。 应力通常定义为单位面积上的力。 当力拉动物体并导致其伸长时,例如松紧带的拉伸,我们将这种应力称为拉伸应力。 当力导致物体压缩时,我们称之为压缩应力。 当物体从四面八方被挤压时,比如潜水艇在海洋深处,我们将这种压力称为体积应力(或体积应力)。 在其他情况下,作用力可能既不是拉伸力也不是压缩力,但仍会产生明显的变形。 例如,假设你将一本书紧紧地放在手掌之间,然后用一只手按住封面并拉开远离你的距离,另一只手向你按下并拉封底。 在这种情况下,当变形力与物体表面切向作用时,我们称之为 “剪切” 力,它们产生的应力称为剪切应力。
应力的 SI 单位是帕斯卡 (Pa)。 当一牛顿的力压在一平方米的单位表面积上时,产生的应力为一帕斯卡:
\[one\; pascal = 1.0\; Pa = \frac{1.0\; N}{1.0\; m^{2}} \ldotp\]
在英国单位制中,应力单位为 “psi”,代表 “磅每平方英寸”(lb/in 2)。 另一个经常用于体积应力的单位是 atm(大气)。 换算系数是
\[1\; psi = 6895\; Pa\; and\; 1\; Pa = 1.450 \times 10^{-4}\; psi\]
\[1\; atm = 1.013 \times 10^{5}\; Pa = 14.7\; psi \ldotp\]
受压的物体或介质会变形。 描述这种变形的量称为应变。 应变以长度(在拉伸应力下)、体积(体积应力下)或几何形状(剪切应力下)的分数变化给出。 因此,应变是一个无量纲的数字。 拉应力下的应变称为拉伸应变,体应力下的应变称为体积应变(或体积应变),由剪应力引起的应变称为剪切应变。
应力越大,应变越大;但是,应变和应力之间的关系不必是线性的。 只有当应力足够低时,它造成的变形才会与应力值成正比。 这种关系中的比例常数称为弹性模量。 在低应力值的线性极限中,应力和应变之间的一般关系为
\[stress = (elastic\; modulus) \times strain \ldotp \label{12.33}\]
从这种关系的维度分析中我们可以看出,弹性模量与应力具有相同的物理单位,因为应变是无量纲的。
我们还可以从方程\ ref {12.33} 中看出,当物体以较大的弹性模量值为特征时,应力的影响很小。 另一方面,较小的弹性模量意味着应力会产生较大的应变和明显的变形。 例如,橡皮筋上的应力比相同尺寸的钢带上的相同应力产生的应变(变形)更大,因为橡胶的弹性模量比钢的弹性模量小两个数量级。
拉应力的弹性模量称为杨氏模量;体积应力的弹性模量称为体积模量;剪应力的弹性模量称为剪切模量。 请注意,应力和应变之间的关系是一种观察到的关系,在实验室中测量。 各种材料的弹性模量是在不同的物理条件(例如温度变化)下测量的,并收集在工程数据表中以供参考(表\(\PageIndex{1}\))。 这些表格是行业和任何参与工程或施工的人的宝贵参考资料。 在下一节中,我们将讨论在直至断裂点的所有应力值范围内,超出方程\ ref {12.33} 表示的线性极限的应变-应力关系。 在本节的其余部分中,我们将研究方程\ ref {12.33} 表示的线性极限。
| 材质 | 杨氏模量 × 10 10 Pa | 体积模量 × 10 10 Pa | 剪切模量 × 10 10 Pa |
|---|---|---|---|
| 铝 | 7.0 | 7.5 | 2.5 |
| 骨头(张力) | 1.6 | 0.8 | 8.0 |
| 骨骼(压缩) | 0.9 | ||
| 黄铜 | 9.0 | 6.0 | 3.5 |
| 砖块 | 1.5 | ||
| 混凝土 | 2.0 | ||
| 铜 | 11.0 | 14.0 | 4.4 |
| 皇冠玻璃 | 6.0 | 5.0 | 2.5 |
| 花岗岩 | 4.5 | 4.5 | 2.0 |
| 头发(人类) | 1.0 | ||
| 硬木 | 1.5 | 1.0 | |
| 铁 | 21.0 | 16.0 | 7.7 |
| 领导 | 1.6 | 4.1 | 0.6 |
| 大理石 | 6.0 | 7.0 | 2.0 |
| 镍 | 21.0 | 17.0 | 7.8 |
| 聚苯乙烯 | 3.0 | ||
| 丝绸 | 6.0 | ||
| 蜘蛛线 | 3.0 | ||
| 钢铁 | 20.0 | 16.0 | 7.5 |
| 丙酮 | 0.07 | ||
| 乙醇 | 0.09 | ||
| 甘油 | 0.45 | ||
| 水星 | 2.5 | ||
| 水 | 0.22 |
拉伸或压缩应力、应变和杨氏模量
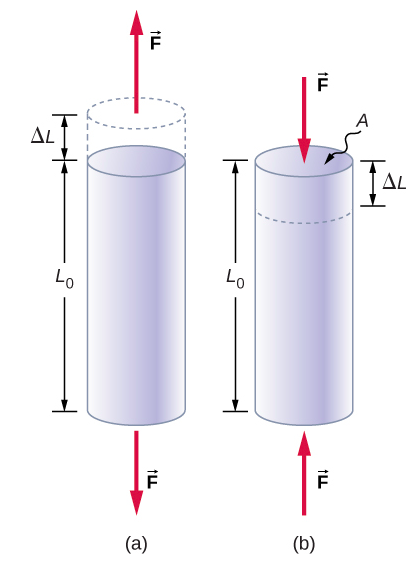
当两个大小相等的反平行力仅沿物体的一个维度作用于物体上,从而使物体不移动时,就会发生张力或压缩。 设想这种情况的一种方法如图所示\(\PageIndex{1}\)。 杆段要么被沿其长度作用并垂直于其横截面的一对力拉伸,要么被挤压。 这种力的净效果是,杆的长度从力出现之前的原始长度 L 0 变为在力作用下的新长度 L。 长度\(\Delta\) L = L − L 0 的变化可能是伸长率(当大\(L\)于原始长度时\(L_o\))或收缩(当 L 小于原始长度 L 0 时)。 当力拉伸物体从而导致其伸长时,就会发生拉伸应力和应变,并且长度变化\(\Delta L\)为正值。 当力收缩物体从而导致其缩短并且长度变化\(\Delta L\)为负值时,就会发生压缩应力和应变。
无论哪种情况,我们都将应力定义为变形力\(F_{\perp}\)与被变形物体的横截面积 A 的比率。 我们为变形力保留的符号 F \(\perp\)表示该力垂直于物体的横截面起作用。 平行于横截面的力不会改变物体的长度。 拉应力的定义是
\[tensile\; stress = \frac{F_{\perp}}{A} \ldotp \label{12.34}\]
拉伸应变是衡量物体在拉应力下变形的量度,定义为物体承受拉应力时物体长度的分数变化
\[tensile\; strain = \frac{\Delta L}{L_{0}} \ldotp \label{12.35}\]
压缩应力和应变分别由相同的公式定义,即方程\ ref {12.34} 和\ ref {12.35}。 与拉伸情况的唯一区别是,对于压缩应力和应变,我们在方程\ ref {12.34} 和\ ref {12.35} 中取右侧的绝对值。
杨氏模量\(Y\)是变形由拉应力或压缩应力引起时的弹性模量,由方程\ ref {12.33} 定义。 将该方程除以拉伸应变,得出杨氏模量的表达式:
\[Y = \frac{tensile\; stress}{tensile\; strain} = \frac{\frac{F_{\perp}}{A}}{\frac{\Delta L}{L_{0}}} = \frac{F_{\perp}}{A} = \frac{L_{0}}{\Delta L} \ldotp \label{12.36}\]
重达 10,000 N 的雕塑位于一个 6.0 米高的垂直柱子顶部的水平表面上\(\PageIndex{1}\)。 柱子的横截面积为 0.20 m 2,由花岗岩制成,质量密度为 2700 kg/m 3。 找出位于柱顶下方 3.0 m 处的横截面的压缩应力以及柱子顶部 3.0 米段的压缩应变值。

策略
首先,我们找到柱子顶部 3.0 米长的重量。 作用于距离顶部向下 3.0 m 的横截面的法向力是柱子的重量和雕塑重量的总和。 获得法向力后,我们使用方程 12.34 来求应力。 为了找到压缩应变,我们在表\(\PageIndex{1}\)和反转方程\ ref {12.36} 中找到了花岗岩杨氏模量的值。
解决方案
高 h = 3.0 m、横截面积 A = 0.20 m 2 的柱段的体积为
\[V = Ah = (0.20\; m^{2})(3.0\; m) = 0.60\; m^{3} \ldotp\]
当花岗岩的密度\(\rho\) = 2.7 x 10 3 kg/m 3 时,柱段的质量为
\[m = \rho V = (2.7 \times 10^{3}\; kg/m^{3})(0.60\; m^{3}) = 1.60 \times 10^{3}\; kg \ldotp\]
支柱段的重量为
\[w_{p} = mg = (1.60 \times 10^{3}\; kg)(9.80\; m/s^{2}) = 1.568 \times 10^{4}\; N \ldotp\]
雕塑的重量为 w s = 1.0 x 10 4 N,因此位于雕塑下方 3.0 米处的横截面上的法向力为
\[F_{\perp} = w_{p} + w_{s} = (1.568 + 1.0) \times 10^{4}\; N = 2.568 \times 10^{4}\; N \ldotp\]
因此,压力是
\[stress = \frac{F_{\perp}}{A} = \frac{2.568 \times 10^{4}\; N}{0.20 m^{2}} = 1.284 \times 10^{5}\; Pa = 128.4\; kPa \ldotp\]
杨氏花岗岩模量为 Y = 4.5 x 10 10 Pa = 4.5 x 10 7 kPa。 因此,该位置的压缩应变为
\[strain = \frac{stress}{Y} = \frac{128.4\; kPa}{4.5 \times 10^{7}\; kPa} = 2.85 \times 10^{-6} \ldotp\]
意义
请注意,作用于柱子横截面积的法向力在其长度上不是恒定的,而是从顶部的最小值到柱子底部的最大值不等。 因此,如果柱子沿其长度具有均匀的横截面积,则其底部的应力最大。
找出纳尔逊柱底部的压缩应力和应变。
一根 2.0 米长的钢棒的横截面积为 0.30 cm 2。 钓竿是垂直支撑的一部分,垂直支撑架支撑着一个 550 千克的沉重平台,该平台悬挂在钓竿的下端。 忽略杆的重量,棒中的拉应力和杆在应力下的伸长率是多少?
策略
首先,我们根据方程式 12.34 计算杆在平台重量下的拉伸应力。 然后我们反转方程式 12.36 以求出杆的伸长率,使用 L 0 = 2.0 m。在表 12.1 中,钢的杨氏模量为 Y = 2.0 x 10 11 Pa。
解决方案
将数值代入方程式可以给我们
\[\begin{split} \frac{F_{\perp}}{A} & = \frac{(550\; kg)(9.8\; m/s^{2})}{3.0 \times 10^{-5}\; m^{2}} = 1.8 \times 10^{8}\; Pa \\ \Delta L & = \frac{F_{\perp}}{A} \frac{L_{0}}{Y} = (1.8 \times 10^{8}\; Pa) \left(\dfrac{2.0\; m}{2.0 \times 10^{11}\; Pa}\right) = 1.8 \times 10^{-3}\; m = 1.8\; mm \ldotp \end{split}\]
意义
与立柱示例中的拉伸应力类似,本示例中的拉伸应力在杆的长度上并不均匀。 但是,与前面的示例不同的是,如果将杆的重量考虑在内,则设备所在杆的顶部应力最大,底部的应力最小。
一根 2.0 米长的电线在承受负荷时会延伸 1.0 mm。 电线中的拉伸应变是多少?
物体通常可以同时承受压缩应力和拉伸应力图\(\PageIndex{3}\)。 一个例子是一个长书架,里面装满了沉重的书,在书的重量下,它在两端支撑之间下垂。 搁板的顶部表面处于压缩应力之下,搁板的底部表面处于拉伸应力状态。 同样,长而沉重的光束在自身的重量下垂。 在现代建筑施工中,使用工字梁图形几乎可以消除这种弯曲应变\(\PageIndex{4}\)。


一个沉重的箱子放在由三列支撑的桌子上。 观看此演示,移动方块,看看方块改变位置时柱中的压缩(或张力)会受到怎样的影响。


