12.3:静态平衡示例
- Page ID
- 204819
- 识别和分析静态平衡情况
- 为处于静态平衡状态的扩展物体设置自由体图
- 设置和求解各种物理环境中处于平衡状态的物体的静态平衡条件
本章中的所有示例都是平面问题。 因此,我们使用方程 12.2.9 到方程 12.2. 11 的分量形式的平衡条件。 我们在示例 12.1 中引入了问题解决策略来说明平衡条件的物理意义。 现在,我们在求解扩展刚体的静态平衡问题时要遵循的步骤列表中概括了这个策略。 我们分五个实际步骤进行。
- 确定要分析的对象。 对于某些处于平衡状态的系统,可能需要考虑多个物体。 识别作用于物体的所有力。 确定您需要回答的问题。 找出问题中提供的信息。 在现实问题中,一些关键信息可能隐含在情境中,而不是明确提供。
- 为物体设置自由体图。 (a) 为问题选择 xy 参考框架。 为物体绘制自由体图,仅包括作用于该物体的力。 如果合适,在所选参考框架中用力分量表示力。 在为每种力执行此操作时,请划掉原始力,这样就不会错误地在方程中两次包含相同的力。 标记所有力-您需要使用它来正确计算 x 和 y 方向上的净力。 对于未知的力量,必须任意分配方向;可以将其视为 “工作方向” 或 “可疑方向”。 正确的方向由您在最终解中获得的符号决定。 加号 (+) 表示工作方向是实际方向。 减号 (−) 表示实际方向与假定工作方向相反。 (b) 选择旋转轴的位置;换句话说,选择用于计算作用力矩的轴心点。 在自由体图上,指明枢轴和作用力的杠杆臂的位置,您将需要它来正确计算扭矩。 在选择枢轴时,请记住,枢轴可以放置在你想要的任何地方,但指导原则是,最佳选择将尽可能简化沿旋转轴净扭矩的计算。
- 为物体设置平衡方程。 (a) 使用自由体图为 x 方向上的力分量写出正确的平衡条件方程 12.2.9。 (b) 使用自由体图为 y 方向上的力分量写出正确的平衡条件方程 12.2.13。 (c) 使用自由体图为沿旋转轴的扭矩写出正确的平衡条件方程 12.2.11。 使用方程 12.2.12 来评估扭矩大小和感应。
- 简化并求解平衡方程组以获得未知量。 此时,你的工作只涉及代数。 请记住,方程的数量必须与未知数的数量相同。 如果未知数的数量大于方程的数量,则无法解决问题。
- 计算您在解中获得的未知量的表达式。 你的最终答案应该有正确的数值和正确的物理单位。 如果不是,则使用前面的步骤将错误追溯到其起源并进行纠正。 此外,你可以通过将枢轴移到其他位置并再次求解问题来独立检查你的数字答案,这就是我们在示例 12.1 中所做的。
请注意,为刚体平衡问题设置自由体图是求解过程中最重要的组成部分。 没有正确的设置和正确的图表,你将无法写下正确的平衡条件。 另请注意,可能经历旋转运动的延伸刚体的自由体图与仅经历平移运动的物体的自由体图不同(如您在牛顿运动定律章节中所看到的那样)。 在平移动力学中,物体以其 CM 表示,其中主体上的所有力都附着,不出现扭矩。 这在旋转动力学中并非如此,在旋转动力学中,延伸的刚体不能仅用一个点来表示。 其原因是,在分析旋转时,我们必须识别作用于身体的扭矩,而扭矩既取决于作用力,也取决于其杠杆臂。 在这里,延伸刚体的自由体图可帮助我们识别外部扭矩。
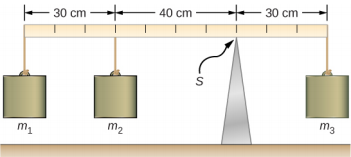
三个质量附着在统一的仪表杆上,如图所示\(\PageIndex{1}\)。 仪表杆的质量为 150.0 g,支点左侧的质量为 m 1 = 50.0 g,m 2 = 75.0 g。找到安装在仪表杆右端时平衡系统的质量 m3,以及系统平衡时支点处的法向反作用力。
策略
对于图中所示的排列方式,我们确定了作用于仪表杆的以下五种力:
- w 1 = m 1 g 是质量重量 m 1;
- w 2 = m 2 g 是质量重量 m 2;
- w = mg 是整根仪表棒的重量;
- w 3 = m 3 g 是未知质量的重量 m 3;
- F S 是支撑点 S 处的法向反作用力。
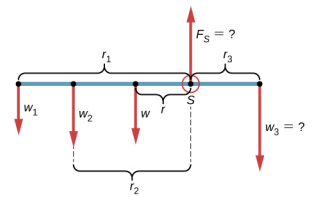
我们选择一个参考系,其中 y 轴的方向是重力方向,x 轴的方向是沿着仪表杆,旋转轴(z 轴)垂直于 x 轴并穿过支撑点 S。换句话说,我们选择枢轴位于仪表棒碰到支架。 这是枢轴的自然选择,因为该点不会随着摇杆的旋转而移动。 现在我们可以为仪表杆设置自由体图了。 我们指示枢轴,然后附加五个向量,代表沿着代表仪表杆的线上的五种力,将力相对于枢轴图进行定位\(\PageIndex{2}\)。 在这个阶段,根据问题中提供的信息,我们可以确定五种力量的杠杆臂。 对于三个悬挂的群众来说,问题显而易见,在于它们在棍子上的位置,但是关于重量 w 的位置的信息是隐含地给出的。 这里的关键词是 “制服”。 从我们之前的研究中我们知道,制服棍的厘米位于其中点,所以这是我们在50厘米标记处附加重量w的地方。
解决方案
以图形\(\PageIndex{1}\)和图形作为参考,我们首先找到作\(\PageIndex{2}\)用于摇杆的五种力的杠杆臂:
\[\begin{split} r_{1} & = 30.0\; cm + 40.0\; cm = 70.0\; cm \\ r_{2} & = 40.0\; cm \\ r & = 50.0\; cm - 30.0\; cm = 20.0\; cm \\ r_{S} & = 0.0\; cm\; (because\; F_{S}\; is\; attached\; at\; the\; pivot) \\ r_{3} & = 30.0\; cm \ldotp \end{split}\]
现在我们可以找到相对于所选枢轴的五个扭矩:
\[\begin{split} \tau_{1} & = +r_{1} w_{1} \sin 90^{o} = +r_{1} m_{1} g \quad (counterclockwise\; rotation,\; positive\; sense) \\ \tau_{2} & = +r_{2} w_{2} \sin 90^{o} = +r_{2} m_{2} g \quad (counterclockwise\; rotation,\; positive\; sense) \\ \tau & = +rw \sin 90^{o} = +rmg \quad \quad \quad (gravitational\; torque) \\ \tau_{S} & = r_{S} F_{S} \sin \theta_{S} = 0 \quad \quad \quad \quad \quad (because\; r_{S} = 0\; cm) \\ \tau_{3} & = -r_{3} w_{3} \sin 90^{o} = -r_{3} m_{3} g \quad (counterclockwise\; rotation,\; negative\; sense) \end{split}\]
仪表杆的第二个平衡条件(扭矩方程)是
\[\tau_{1} + \tau_{2} + \tau + \tau_{S} + \tau_{3} = 0 \ldotp\]
将扭矩值代入这个方程式时,我们可以省略贡献为零的扭矩。 这样,第二个平衡条件是
\[+r_{1} m_{1} g + r_{2} m_{2} g + rmg - r_{3} m_{3} g = 0 \ldotp \label{12.17}\]
选择与之平行的 +y 方向\(\vec{F}_{S}\),摇杆的第一个平衡条件是
\[-w_{1} - w_{2} - w + F_{S} - w_{3} = 0 \ldotp\]
用力代替,第一个平衡条件变成
\[-m_{1} g - m_{2} g - mg + F_{S} - m_{3} g = 0 \ldotp \label{12.18}\]
我们同时求解这些方程以获得未知值 m 3 和 F S。 在方程\ ref {12.17} 中,我们取消 g 因子并重新排列项以获得
\[r_{3} m_{3} = r_{1} m_{1} + r_{2} m_{2} + rm \ldotp\]
为了得到 m 3,我们将两边除以 r 3,所以我们有
\[\begin{split} m_{3} & = \frac{r_{1}}{r_{3}} m_{1} + \frac{r_{2}}{r_{3}} m_{2} + \frac{r}{r_{3}} m \\ & = \frac{70}{30} (50.0\; g) + \frac{40}{30} (75.0\; g) + \frac{20}{30} (150.0\; g) = 315.0 \left(\dfrac{2}{3}\right)\; g \simeq 317\; g \ldotp \end{split} \label{12.19}\]
为了找到法向反作用力,我们重新排列了方程\ ref {12.18} 中的项,将克转换为千克:
\[\begin{split} F_{S} & = (m_{1} + m_{2} + m + m_{3}) g \\ & = (50.0 + 75.0 + 150.0 + 316.7) \times (10^{-3}\; kg) \times (9.8\; m/s^{2}) = 5.8\; N \ldotp \end{split} \label{12.20}\]
意义
请注意,方程\ ref {12.17} 与 g 的值无关。因此,扭矩平衡可用于测量质量,因为地球表面 g 值的变化不会影响这些测量。 弹簧摆轮并非如此,因为它可以测量力。
使用仪表杆的左端重复示例 12.3 来计算扭矩;也就是说,将枢轴放在仪表杆的左端。
在下一个示例中,我们展示了如何使用方程 12.2. 9 和方程 12. 2.10 给出的矢量形式的第一个平衡条件(力方程)。 我们提出这个解决方案是为了说明选择合适的参考框架的重要性。 尽管所有惯性参考系都是等效的,并且在一个帧中获得的数值解与任何其他帧中获得的数值解相同,但选择不合适的参考系会使解变得相当冗长和复杂,而明智地选择参考系会使解变得直截了当。 我们在同一个问题的等效解决方案中展示了这一点。 这个特殊的例子说明了静态平衡在生物力学中的应用。
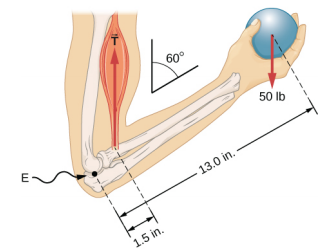
举重运动员的前臂重量为50.0磅(相当于222.4 N),如图所示\(\PageIndex{3}\)。 他的前臂相对于上臂的位置为\(\beta\) = 60°。 前臂由二头肌肌肉收缩支撑,这会导致肘部周围产生扭矩。 假设二头肌的张力沿着重力给出的垂直方向起作用,那么肌肉必须施加什么张力才能将前臂保持在所示的位置? 肘关节的力量是多少? 假设前臂的重量可以忽略不计。 以 SI 为单位给出最终答案。
策略
我们确定了作用于前臂的三种力\(\vec{F}\):肘部的未知力;肌肉\(\vec{T}_{M}\)中的未知张力;以及大小为 w = 50 磅的重量\(\vec{w}\)。我们采用参考框架,x 轴沿前臂,枢轴位于肘部。 垂直方向是重量的方向,与上臂的方向相同。 x 轴使垂直角度\(\beta\) = 60°。 y 轴垂直于 x 轴。 现在我们为前臂设置自由体图。 首先,我们绘制轴、枢轴和代表三种已确定的力的三个向量。 然后我们找到角度\(\beta\)并用 x 和 y 分量表示每种力,记得划掉原始力向量以避免重复计数。 最后,我们给部队及其杠杆臂贴上标签。 前臂的自由体图如图所示\(\PageIndex{4}\)。 此时,我们已经准备好为前臂设置平衡条件了。 每种力都有 x 和 y 分量;因此,我们有两个方程表示第一个平衡条件,一个方程表示作用于前臂的净力的每个分量。
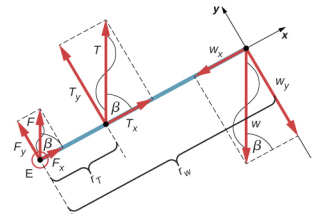
请注意,在我们的参考框架中,对第二个平衡条件(扭矩)的贡献仅来自力的 y 分量,因为力的 x 分量都平行于其杠杆臂,因此对于其中任何一个条件,我们在方程 12.2.12 中都有 sin\(\theta\) = 0。 对于 y 分量,我们在方程 12.2.12 中得出\(\theta\) = ± 90°。 另请注意,肘部的力的扭矩为零,因为该力附着在枢轴上。 因此,对净扭矩的贡献仅来自 T y 和 w y 的扭矩。
解决方案
从自由体图中我们可以看出,净力的 x 分量满足方程
\[+F_{x} + T_{x} - w_{x} = 0 \label{12.21}\]
并且净力的 y 分量满足
\[+F_{y} + T_{y} - w_{y} = 0 \ldotp \label{12.22}\]
方程\ ref {12.21} 和方程\ ref {12.22} 是第一个平衡条件(用于力)的两个方程。 接下来,我们从自由体图中看出,沿旋转轴的净扭矩为
\[+r_{T} T_{y} - r_{w} w_{y} = 0 \ldotp \label{12.23}\]
方程\ ref {12.23} 是前臂的第二个平衡条件(扭矩)。 自由体图显示,杠杆臂为 r T = 1.5 英寸,r w = 13.0 英寸。 此时,我们不需要将英寸转换为 SI 单位,因为只要这些单位在方程式 12.23 中保持一致,它们就会抵消。 再次使用自由体图,我们可以找到分量力的大小:
\[\begin{split} F_{x} & = F \cos \beta = F \cos 60^{o} = \frac{F}{2} \\ T_{x} & = T \cos \beta = T \cos 60^{o} = \frac{T}{2} \\ w_{x} & = w \cos \beta = w \cos 60^{o} = \frac{w}{2} \\ F_{y} & = F \sin \beta = F \sin 60^{o} = \frac{F \sqrt{3}}{2} \\ T_{y} & = T \sin \beta = T \sin 60^{o} = \frac{T \sqrt{3}}{2} \\ w_{y} & = w \sin \beta = w \sin 60^{o} = \frac{w \sqrt{3}}{2} \ldotp \end{split}\]
我们将这些量级替换为方程\ ref {12.21}、方程\ ref {12.22} 和方程\ ref {12.23},分别得到
\[\begin{split} \frac{F}{2} + \frac{T}{2} - \frac{w}{2} & = 0 \\ \frac{F \sqrt{3}}{2} + \frac{T \sqrt{3}}{2} - \frac{w \sqrt{3}}{2} & = 0 \\ \frac{r_{T} T \sqrt{3}}{2} - \frac{r_{w} w \sqrt{3}}{2} & = 0 \ldotp \end{split}\]
当我们简化这些方程时,我们会发现我们只剩下两个未知力大小 F 和 T 的独立方程,因为 x 分量的方程\ ref {12.21} 等同于 y 分量的方程\ ref {12.22}。 通过这种方式,我们获得了力的第一个平衡条件
\[F + T - w = 0 \label{12.24}\]
以及扭矩的第二个平衡条件
\[r_{T} T - r_{w} w = 0 \ldotp \label{12.25}\]
肌肉张力大小是通过求解方程\ ref {12.25} 得出的:
\[T = \frac{r_{w}}{r_{T}} w =frac{13.0}{1.5} (50\; lb) = 433 \frac{1}{3}\; lb \simeq 433.3\; lb \ldotp\]
肘部的力是通过求解方程\ ref {12.24} 获得的:
\[F = w - T = 50.0\; lb - 433.3\; lb = -383.3\; lb \ldotp\]
方程中的负号告诉我们,肘部的实际力与绘制自由体图时采用的工作方向反平行。 在最终答案中,我们将力转换为 SI 的力单位。 答案是
\[F = 383.3\; lb = 383.3(4.448\; N) = 1705\; N\; downward\]
\[T = 433.3\; lb = 433.3(4.448\; N) = 1927\; N\; upward \ldotp\]
意义
这里有两个重要问题值得注意。 第一个问题涉及到 SI 单位的转换,只要我们保持单位的一致性,就可以在解的最后完成。 第二个重要问题涉及肘部等铰链接头。 在对问题的初步分析中,应始终假定铰链接头向任意方向施加力,然后必须独立求解铰链力的所有分量。 在这个例子中,肘部力恰好是垂直的,因为问题假设二头肌的张力也是垂直的。 但是,这种简化不是一般规则。
解决方案 2
假设我们采用一个参考框架,其中 y 轴的方向沿着 50 磅的重量而枢轴位于肘部。 在此帧中,所有三个力都只有 y 分量,因此对于第一个平衡条件(力),我们只有一个方程。 我们绘制了前臂的自由体图,如图所示\(\PageIndex{5}\),表示枢轴、作用力及其杠杆臂相对于枢轴,以及力\(\vec{T}_{M}\)和\(\vec{w}\)(分别)用杠杆臂形成的角度\(\theta_{T}\)和角度。\(\theta_{w}\) 在方程式 12.2.12 给出的扭矩定义中,角度\(\theta_{T}\)是向量的方向角\(\vec{T}_{M}\),从始终指向远离枢轴的杠杆臂的径向方向逆时针计算。 按照同样的惯例,角度\(\theta_{w}\)是从杠杆臂的径向方向逆时针测量到矢量的\(\vec{w}\)。 这样,非零扭矩最容易通过直接代入方程式 12.2.12 来计算,如下所示:
\[\tau_{T} = r_{T} T \sin \theta_{T} = r_{T} T \sin \beta = r_{T} T \sin 60^{o} = + \frac{r_{T} T \sqrt{3}}{2}\]
\[\tau_{w} = r_{w} w \sin \theta_{w} = r_{w} w \sin (\beta + 180^{o}) = -r_{w} w \sin \beta = - \frac{r_{w} w \sqrt{3}}{2} \ldotp\]
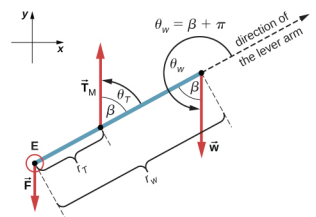
第二个平衡条件\(\tau_{T}\) +\(\tau_{w}\) = 0 现在可以写成
\[\frac{r_{T} T \sqrt{3}}{2} - \frac{r_{w} w \sqrt{3}}{2} = 0 \ldotp \label{12.26}\]
根据自由体图,第一个平衡条件(力)是
\[-F + T - w = 0 \ldotp \label{12.27}\]
方程\ ref {12.26} 与方程\ ref {12.25} 相同,给出的结果 T = 433.3 磅。方程\ ref {12.27} 给出
\[F = T - w = 433.3\; lb - 50.0\; lb = 383.3\; lb\]
我们看到这些答案与我们之前的答案相同,但是参考框架的第二种选择会产生更简单、更快捷的等效解,因为它不需要将力分解为矩形分量。
重复示例 12.4 假设前臂是密度均匀的物体,重 8.896 N
统一的梯子长 L = 5.0 m,重 400.0 N。梯子靠在湿滑的垂直墙上,如图所示\(\PageIndex{6}\)。 梯子和粗糙地板之间的倾角为\(\beta\) = 53°。 找出来自地板和梯子墙壁的反作用力,以及梯子与地板交界\(\mu_{s}\)处防止梯子滑动的静摩擦系数。
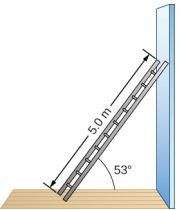
策略
我们可以识别作用于梯子的四种力。 第一力是来自地板向上垂直方向的法向反作用力 N。 第二种力是静摩擦力 f =\(\mu_{s}\) N 沿着地板水平指向墙壁——这种力可以防止梯子滑动。 这两种力量在梯子与地板的接触点作用于梯子。 第三种力是梯子的重量 w,它附着在梯子两端中间的 CM 处。 第四个力是来自墙壁的法向反作用力 F,在水平方向上远离墙壁,附着在与墙的接触点处。 没有其他力量,因为墙很滑,这意味着墙和梯子之间没有摩擦。 基于此分析,我们采用参考框架,y轴在垂直方向(平行于墙),x轴在水平方向(平行于地板)。 在此框架中,每种力要么有水平分量,要么有垂直分量,但不能两者兼而有之,这简化了求解。 我们在与地板的接触点处选择枢轴。 在梯子的自由体图中,我们指出了枢轴、所有四种力及其杠杆臂,以及杠杆臂和力之间的角度,如图所示\(\PageIndex{7}\)。 在我们选择枢轴位置时,无论是来自法向反作用力 N 还是来自静态摩擦 f 的扭矩,因为它们都作用于枢轴。
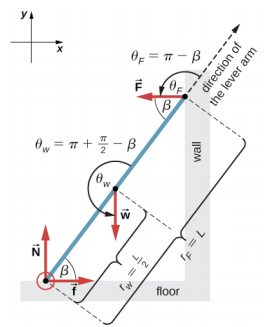
解决方案
根据自由体图,x 方向上的净力为
\[+f - F = 0 \label{12.28}\]
y 方向上的净力为
\[+ N - w = 0 \label{12.29}\]
并且沿旋转轴在枢轴点处的净扭矩为
\[\tau_{w} + \tau_{F} = 0 \ldotp \label{12.30}\]
其中\(\tau_{w}\)是重量 w 的扭矩,\(\tau_{F}\)是反应的扭矩 F。从自由体图中,我们可以确定墙上反作用力的杠杆臂为 r F = L = 5.0 m,重物的杠杆臂为 r w\(\frac{L}{2}\) = 2.5 m。自由体图,我们确定了方程12.2.12 中用于扭矩的角度:\(\theta_{F}\)= 180° −\(\beta\) 表示来自与壁的反作用力的扭矩,\(\theta_{w}\)= 180° +(90° −\(\beta\))表示重量引起的扭矩。 现在我们可以使用方程式 12.2.12 来计算扭矩了:
\[\tau_{w} = r_{w} w \sin \theta_{w} = r_{w} w \sin (180^{o} + 90^{o} - \beta) = - \frac{L}{2} w \sin (90^{o} - \beta) = - \frac{L}{2} w \cos \beta\]
\[tau_{F} = r_{F} F \sin \theta_{F} = r_{F} F \sin (180^{o} - \beta) = LF \sin \beta \ldotp\]
我们将扭矩代入方程\ ref {12.30} 然后求解 F:
\[- \frac{L}{2} w \cos \beta + LF \sin \beta = 0 \label{12.31}\]
\[F = \frac{w}{2} \cot \beta = \frac{400.0\; N}{2} \cot 53^{o} = 150.7\; N\]
我们通过求解方程\ ref {12.29}:N = w = 400.0 N 来获得与地板的法向反作用力。摩擦大小是通过求解方程\ ref {12.28}:f = F = 150.7 N 得出静摩擦系数为\(\mu_{s}\)\(\frac{f}{N}\)\(\frac{150.7}{400.0}\) = = 0.377。
梯子与地板接触点处的净力是来自地板的法向反作用和静摩擦力的矢量和:
\[\vec{F}_{floor} = \vec{f} + \vec{N} = (150.7\; N)(- \hat{i}) + (400.0\; N)(+ \hat{j}) = (-150.7\; \hat{i} + 400.0\; \hat{j}) N \ldotp\]
它的大小是
\[F_{floor} = \sqrt{f^{2} + N^{2}} = \sqrt{150.7^{2} + 400.0^{2}}\; N = 427.4\; N\]
它的方向是
\[\varphi = \tan^{-1} \left(\dfrac{N}{f}\right) = \tan^{-1} \left(\dfrac{400.0}{150.7}\right) = 69.3^{o}\; above\; the\; floor \ldotp\]
我们应该在这里强调两个具有实际用途的一般性意见。 首先,请注意,当我们选择枢轴点时,没有人期望系统实际上会围绕所选点旋转。 本例中的梯子根本不旋转,而是牢固地站在地板上;尽管如此,它与地板的接触点还是枢轴的不错选择。 其次,请注意,当我们使用方程式 12.2.12 来计算单个扭矩时,我们不需要将力分解为相对于杠杆臂方向的法向和平行分量,也不需要考虑扭矩感。 只要在自由体图的帮助下正确识别方程 12.2.12 中的角度,即从杠杆臂方向到力向量方向逆时针测量的角度,方程 12.2.12 就会给出扭矩的大小和感觉。 这是因为扭矩是杠杆臂向量与力矢量交叉的矢量乘积,公式 12.2.12 表示该矢量乘积沿旋转轴的矩形分量。
意义
该结果与梯子的长度无关,因为 L 在第二个平衡条件下被取消,即方程\ ref {12.31}。 无论梯子有多长或多短,只要它的重量为 400 N,与地板的角度为 53°,我们的结果都保持不变。 但是,如果方程式\ ref {12.31} 中的净扭矩变为负值,梯子就会滑动。 当静摩擦系数不足以防止梯子滑动时,在某些角度会发生这种情况。
对于示例 12.5 中描述的情况,假定 β 是梯子与地板\(\mu_{s}\)的角度,请确定梯子开始滑动的静摩擦系数的值。
重量为 w = 400.0 N 的摆动门由铰链 A 和 B 支撑,因此门可以绕穿过铰链的垂直轴摆动\(\PageIndex{8}\)。 门的宽度为 b = 1.00 m,门板的质量密度均匀。 铰链对称地放置在门的边缘,使门的重量在它们之间均匀分布。 铰链之间的距离为 a = 2.00 m。找出门半开时铰链上的力。
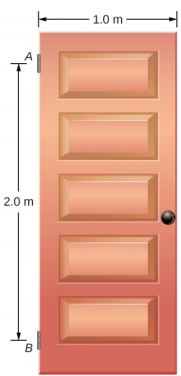
策略
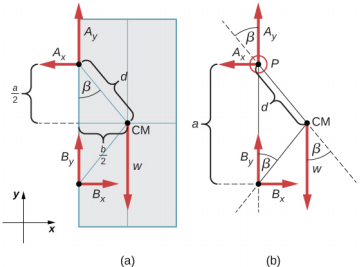
只要反转铰链对门施加的力的方向,就可以找到门对铰链施加的力。 因此,我们的任务是从门上的铰链中找到力量。 三种力作用在门板上:\(\vec{A}\)来自铰链 A 的未知力、\(\vec{B}\)来自铰链 B 的未知力以及\(\vec{w}\)附着在门板质心的已知重量。 CM 位于门的几何中心,因为板具有均匀的质量密度。 我们采用矩形参照系,y轴沿重力方向,x轴位于板的平面上,如图中的面板 (a) 所示\(\PageIndex{9}\),并将所有力分解为矩形分量。 这样,我们就有了四个未知分量力:两个力分量\(\vec{A}\)(A x 和 A y)和两个力分量\(\vec{B}\)(B x 和 B y)。 在自由体图中,我们用其向量分量表示铰链处的两种力,它们的假定方向是任意的。 因为有四个未知数(A x、B x、A y 和 B y),所以我们必须设置四个独立方程。 一个方程是 x 方向上的力的平衡条件。 第二个方程是 y 方向上的力的平衡条件。 第三个方程是绕铰链旋转扭矩的平衡条件。 因为重量在铰链之间均匀分布,所以我们有第四个方程,A y = B y。 为了设置平衡条件,我们绘制了一张自由体图,然后在上部铰链处选择枢轴点,如图面板 (b) 所示\(\PageIndex{9}\)。 最后,我们求解未知力分量的方程并找到力。
解决方案
从门的自由体图中,我们可以得出力量的第一个平衡条件:
在 x 方向上,$$-A_ {x} + B_ {x} = 0\ Rightarrow A_ {x} + B_ {x} $in y 方向,$$+ A_ {y} + B_ {y}-w = 0\ Rightarrow A_ {y} =\ frac {w} {2} =\ frac {400.0\; N} {2} = 200.0\; N\ ldotp\]
我们在点 P(根据自由体图,上部铰链)处选择枢轴,然后写下围绕点 P 旋转扭矩的第二个平衡条件:
pivot at P: $$\ tau_ {w} +\ tau_ {Bx} +\ tau_ {By} = 0\ ldotp\ label {12.32}\]
我们使用自由体图来找出这个方程中的所有项:
\[\begin{split} \tau_{w} & = dw \sin (- \beta) = -dw \sin \beta = -dw \frac{\frac{b}{2}}{d} = -w \frac{b}{2} \\ \tau_{Bx} & = a B_{x} \sin 90^{o} = + a B_{x} \\ \tau_{By} & = a B_{y} \sin 180^{o} = 0 \ldotp \end{split}\]
在计算 sin 时\(\beta\),我们使用图 (a) 部分所示的三角形的几何形状。 现在我们将这些扭矩替换为方程\ ref {12.32} 并计算 B x:
pivot at P: $$-w\ frac {b} {2} + a B_ {x} = 0\ Rightarrow B_ {x} = w\ frac {b} {2a} = (400.0\; N)\ frac {1} {2\;\ cdotp 2} = 100.0\; N\ ldotp\]
因此,水平分量力的大小为 A x = B x = 100.0 N。门上的力是
上部铰链处:$$\ vec {F} _ {A\; on\; n\; N\;\ hat {i} + 200.0\; N\;\ hat {j} $$at 下铰链:$$\ vec {F} _ {B\; on\; n\; N\;\ hat {i} + 200.0; N\;\ hat {j}\ ldotp\]
铰链上的力是根据牛顿第三定律得出的
上部铰链上:$$\ vec {F} _ {door\; on\; A} = 100.0\; N\;\ hat {i}-200.0\; N\;\ hat {j} $在下铰链上:$$\ vec {F} _ {door\; on\; N\;\ hat {i}-200.0\; N\;\ hat {j}\ ldotp\]
意义
请注意,如果在没有假设两个铰链之间的重量分布相等的情况下提出问题,我们将无法求解,因为未知数的数量将大于表示平衡条件的方程的数量。
通过在质心处取枢轴位置来解决示例 12.6 中的问题。
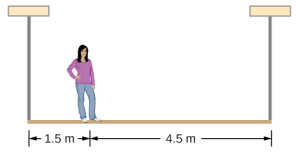
一个50公斤的人站在距离一个质量为70.0千克的6.0米长的统一脚手架的一端1.5米处。 找出支撑脚手架的两根垂直绳索中的张力。
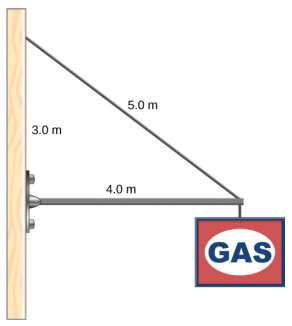
制服支柱末端悬挂着一个 400.0-N 的标志。 支柱长 4.0 米,重 600.0 N。支柱由墙上的铰链和电缆支撑,电缆的另一端在支柱左端 3.0 米处绑在墙上。 找出支撑电缆中的张力和支柱上铰链的力。