12.2：静态平衡的条件

Last updated
Save as PDF

Page ID: 204803

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

学习目标

确定静态平衡的物理条件。
绘制受力作用的刚体的自由体图。
解释平衡条件如何允许我们解决静力学问题。

我们说，当刚体的线性加速度和角加速度相对于惯性参照系均为零时，刚体处于平衡状态。这意味着处于平衡状态的物体可以移动，但如果是的话，它的线速度和角速度必须是恒定的。我们说刚体在我们选定的参照系中处于静止状态时处于静止状态。请注意，静止状态和均匀运动状态之间的区别是人为的——也就是说，物体可能在我们选定的参考系中处于静止状态，但是对于相对于我们的帧以恒定速度移动的观察者来说，同一个物体似乎处于恒定速度的均匀运动。因为运动是相对的，所以对我们来说处于静态平衡状态的东西与移动的观察者处于动态平衡，反之亦然。由于所有惯性参考系的物理定律都是相同的，因此在惯性参考系中，静态平衡和平衡之间没有区别。

根据牛顿第二运动定律，刚体的线性加速度是由作用在其上的净力引起的，或者

\[\sum_{k} \vec{F}_{k} = m \vec{a}_{CM} \ldotp \label{12.1}\]

这里，是作用于物体的所有外力的总和，其中 m 是其质量，是其质心的线性加速度（我们在《线性动量和碰撞》中讨论的关于线性动量和碰撞的概念）。\(\vec{a}_{CM}\) 在平衡状态下，线性加速度为零。如果我们在方程\ ref {12.1} 中将加速度设置为零，则得到以下方程：

第一个平衡条件

刚体静态平衡的第一个平衡条件表示平移平移平衡：

\[\sum_{k} \vec{F}_{k} = \vec{0} \ldotp \label{12.2}\]

第一个平衡条件是方程\ ref {12.2}，是我们在研究牛顿定律应用时遇到的力的平衡条件。

此向量方程等同于净力分量的以下三个标量方程：

\[\sum_{k} F_{kx} = 0,\; \sum_{k} F_{ky} = 0,\; \sum_{k} F_{kz} = 0 \ldotp \label{12.3}\]

与方程\ ref {12.1} 类似，我们可以说刚体绕固定旋转轴\(\vec{\alpha}\)的旋转加速度是由作用在主体上的净扭矩引起的，或者

\[\sum_{k} \vec{\tau}_{k} = I \vec{\alpha} \ldotp \label{12.4}\]

这里 I 是主体绕该轴旋转时的旋转惯性，总和是方程\ ref {12.2} 中所有外力扭矩\(\vec{\tau}_{k}\)的总和。在平衡状态下，旋转加速度为零。通过将方程\ ref {12.4} 的右侧设置为零，我们得到第二个平衡条件：

第二个平衡条件

刚体静态平衡的第二个平衡条件表示旋转平衡：

\[\sum_{k} \vec{\tau}_{k} = \vec{0} \ldotp \label{12.5}\]

第二个平衡条件是方程\ ref {12.5}，是我们在研究旋转动力学时遇到的扭矩的平衡条件。值得注意的是，这种平衡方程通常适用于围绕任何旋转轴（固定或其他方式）的旋转平衡。同样，这个向量方程等同于净扭矩的矢量分量的三个标量方程：

\[\sum_{k} \tau_{kx} = 0,\; \sum_{k} \tau_{ky} = 0,\; \sum_{k} \tau_{kz} = 0 \ldotp \label{12.6}\]

第二个平衡条件意味着在平衡状态下，没有净外部扭矩导致绕任何轴旋转。第一和第二平衡条件在特定的参考系中陈述。第一个条件仅涉及力，因此与参考系的原点无关。但是，第二个条件涉及扭矩，扭矩被定义为十字积\(\vec{\tau}_{k} = \vec{r}_{k} \times \vec{F}_{k}\)，其中\(\vec{r}_{k}\)相对于施加力点旋转轴的位置向量进入方程。因此，扭矩取决于轴在参考系中的位置。但是，当旋转和平移平衡条件同时保持在一个参考系中时，它们也保持在任何其他惯性参考系中，因此围绕任何旋转轴的净扭矩仍然为零。对此的解释相当简单。

假设向量\(\vec{R}\)是旧惯性参考系 S 中新的惯性参考系 S′ 的原点位置。根据我们对相对运动的研究，我们知道在新的参考系 S′ 中，施加力的\(\vec{F}_{k}\)点\(\vec{r}′_{k}\)的位置向量为\(\vec{r}_{k}\)通过方程与之相关

\[\vec{r}'_{k} = \vec{r}_{k} - \vec{R} \ldotp\]

现在，我们可以在新的参考系中汇\(\vec{\tau}'_{k} = \vec{r}'_{k} \times \vec{F}_{k}\)总所有外力的所有扭矩，S'：

\[\sum_{k} \vec{\tau}'_{k} = \sum_{k} \vec{r}'_{k} \times \vec{F}_{k} = \sum_{k} (\vec{r}_{k} - \vec{R}) \times \vec{F}_{k} = \sum_{k} \vec{r}_{k} \times \vec{F}_{k} - \sum_{k} \vec{R} \times \vec{F}_{k} = \sum \vec{\tau}_{k} - \vec{R} \times \sum_{k} \vec{F}_{k} = \vec{0} \ldotp\]

在这条推理链的最后一步中，我们使用了这样一个事实，即在旧参考框架 S 中的平衡中，第一个项因方程\ ref {12.5} 而消失，第二个项因方程\ ref {12.2} 而消失。因此，我们可以看到，只要两个平衡条件都保持在惯性参考系中\ ref {S}，则任何惯性参考系 S′ 中的净扭矩均为零。

其实际含义是，在对刚体应用平衡条件时，我们可以自由选择任何点作为参考系的原点。我们对参考框架的选择取决于我们正在解决的问题的物理特性。在一个参考框架中，平衡条件的数学形式可能相当复杂，而在另一个参考框架中，相同的条件可能具有更简单的数学形式，易于求解。选定参考系的原点称为轴心点。

在最常见的情况下，平衡条件由六个标量方程（方程\ ref {12.3} 和\ ref {12.6}）表示。对于我们在本章中考虑的绕固定轴旋转的平面平衡问题，我们可以将方程的数量减少到三个。标准程序是采用参考框架，其中 z 轴是旋转轴。选择这种轴后，净扭矩只有一个 z 分量，所有扭矩不为零的力都位于 xy 平面中，因此净扭矩的贡献仅来自外力的 x 和 y 分量。因此，对于旋转轴垂直于 xy 平面的平面问题，我们在力和扭矩方面有以下三个平衡条件：

\[F_{1x} + F_{2x} + \cdots + F_{Nx} = 0 \label{12.7}\]

\[F_{1y} + F_{2y} + \cdots + F_{Ny} = 0 \label{12.8}\]

\[\tau_{1} + \tau_{2} + \cdots + \tau_{N} = 0 \label{12.9}\]

其中，总和是作用于身体及其扭矩的所有 N 个外力。在方程\ ref {12.9} 中，我们通过删除下标 z 来简化表示法，但我们在这里理解，求和是沿 z 轴（即旋转轴）的所有贡献。在方程\ ref {12.9} 中，\(\vec{\tau}_{k}\)来自力的扭矩的 z 分量\(\vec{F}_{k}\)为

\[\tau_{k} = r_{k} F_{k} \sin \theta \label{12.10}\]

其中 r _k 是力杠杆臂的长度，F _k 是力的大小（如你在固定轴旋转中看到的那样）。角度\(\theta\)是向量\(\vec{r}_{k}\)与之间的角度\(\vec{F}_{k}\)，沿逆时针方向从\(\vec{r}_{k}\)一个矢量\(\vec{F}_{k}\)到另一个矢量进行测量（图\(\PageIndex{1}\)）。使用方程\ ref {12.10} 时，我们通常会计算扭矩的大小并将其感应分配为正 (+) 或负 (−)，具体取决于仅由此扭矩引起的旋转方向。在方程\ ref {12.9} 中，净扭矩是项的总和，每个项根据方程\ ref {12.10} 计算，每个项的含义必须正确。同样，在方程\ ref {12.7} 中，我们将 + 符号分配给 + x 方向上的力分量，将 − 符号分配给 − x 方向上的分量。计算沿 y 轴的力分量时，在方程\ ref {12.8} 中必须始终遵循相同的规则。

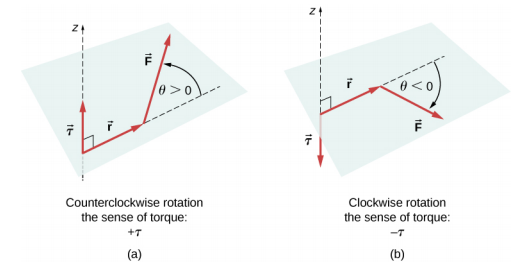
图 A 是导致绕轴逆时针旋转或旋转的力的扭矩示意图。向量 tau 与 Z 轴对齐并具有正值。由向量 F 和 r 形成的角度 theta 大于零。图 B 是导致绕轴顺时针旋转或旋转的力的扭矩示意图。向量 tau 与 Z 轴对齐并具有负值。由向量 F 和 r 形成的角度 theta 小于零。 — 图\(\PageIndex{1}\)：力的扭矩：（a）当力的扭矩导致绕旋转轴逆时针旋转时，我们说它的感应为正，这意味着扭矩矢量平行于旋转轴。 (b) 当力的扭矩导致绕轴顺时针旋转时，我们说它的感应为负，这意味着扭矩矢量与旋转轴反平行。

注意

观看此演示，看看两个力在二维的刚性正方形上起作用。在任何时候，方程\ ref {12.7} 通过方程\ ref {12.9} 给出的静态平衡条件都得到满足。你可以改变力及其杠杆臂的大小，观察这些变化对正方形的影响。

在许多平衡情况下，作用于身体的力量之一是其重量。在自由体图中，权重向量附加到物体的重心上。出于所有实际目的，重心与质心相同，正如你在关于线性动量和碰撞的线性动量和碰撞中学到的那样。只有在物体具有较大的空间延伸以致引力场在其整个体积中不均匀的情况下，重心和质心才会位于不同的点。但是，在实际情况下，即使是像建筑物或游轮这样大的物体也位于地球表面的均匀引力场中，重力引起的加速度的恒定幅度为g = 9.8 m/s ²。在这些情况下，重心与质心相同。因此，在本章中，我们使用质心 (CM) 作为附加权重向量的点。回想一下，CM 具有特殊的物理意义：当外力正好在其 CM 处施加外力时，整个身体会经历平移运动，这种力不会导致旋转。

当 CM 偏离旋转轴时，物体上会产生净重力矩。重力扭矩是重量引起的扭矩。如果没有支撑物体来平衡物体，这种重力扭矩可能会使物体旋转。重力扭矩的大小取决于 CM 离枢轴的距离。例如，对于自卸卡车（图\(\PageIndex{2}\)），枢轴位于轮胎与路面接触的线上。如果 CM 位于路面上方的高处，则重力扭矩可能足够大，足以使卡车翻转。与卡车相比，靠近人行道的 CM 低洼的乘用车更耐翻倒。

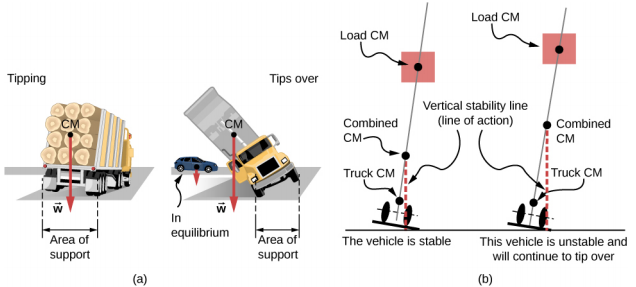
图 A 显示了重心在支撑区域内装载均匀的卡车。图 B 显示了一辆重心位于支撑区域之外且接近翻转的卡车。为了比较，旁边显示了一辆处于平衡状态的汽车。图 C 是示意图，显示了两个车轮之间的组合质心（负载和卡车质心的组合）的位置，用于保持车辆稳定。图 D 是示意图，显示了组合质心（负载质心和卡车质心的组合）在两个轮子之外的位置，这两个轮子会使车辆变得不稳定并可能导致其翻倒。 — 图\(\PageIndex{2}\)：质量的分布会影响质心 (CM) 的位置，权重矢量附着\(\vec{w}\)在那里。如果重心在支撑区域内，则卡车倾斜后会返回到其初始位置 [见 (b) 中的左面板]。但是，如果重心位于支撑区域之外，卡车就会翻身 [见 (b) 中的右侧面板]。 (b) 中的两辆车都失去了平衡。注意（a）中的汽车处于平衡状态：其重心的低位置使其难以翻倒。

注意

如果你倾斜一个方块，使一个边缘与它下面的桌子保持接触，那么支撑底部的一条边缘就会变成枢轴。只要箱子的重心保持在支撑底部上方，重力扭矩就会使盒子向其最初的稳定平衡位置旋转。当重心移动到支撑底部之外时，重力扭矩会使盒子朝相反的方向旋转，盒子会翻过来。观看此演示，尝试盒子的稳定和不稳定位置。

示例 12.1：汽车的重心

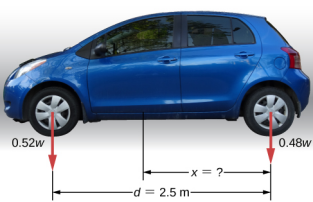
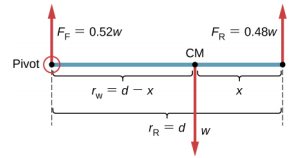
如图 12.4 所示，轴距为 2.5 米的乘用车将 52% 的重量放在平坦地面的前轮上。这辆车相对于后轴的 CM 在哪里？

图为一辆轴距为2.5米的乘用车，其52％的重量在前轮上，48％的重量在平坦地面上的后轮上。后轴和质心之间的距离为 x。 — 图\(\PageIndex{3}\)：汽车车轴之间的重量分布。重心在哪里？

策略

我们不知道汽车的重量。我们所知道的是，当汽车停在水平表面上时，0.52w在前轮的接触点向下推表面，0.48w在后轮的接触点向下推表面。 _{此外，接触点之间的距离为 d = 2.5 m。在这些接触点上，汽车在前桥和后轴上分别承受正常的反作用力，其幅度分别为 F F = 0.52w 和 F _R = 0.48w。} 我们还知道，汽车是刚体处于平衡状态的一个例子，其全部重量 w 作用于其 CM。 CM 位于法向反作用力作用的点之间的某个地方，距离 F _R 作用的点有 x 的距离。我们的任务是找出 x。因此，我们确定作用于车身（汽车）的三种力，然后我们可以绘制延伸刚体的自由体图，如图所示\(\PageIndex{4}\)。

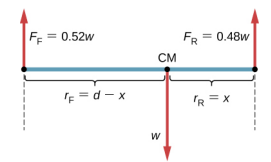
图为示意图，显示轴距定义为 d 的乘用车的质量分布。汽车 52% 的重量在前轮（标记为 Ff）上，48% 的重量在后轮（标有 Fr）上，并且位于平坦的地面上。后轴和质心（标记为 rR）之间的距离为 x。前轴和质心（标记为 rF）之间的距离为 d-x。 — 图\(\PageIndex{4}\)：汽车的自由车身图清楚地显示了作用于汽车的力矢量和到质心 (CM) 的距离。当选择 CM 作为枢轴点时，这些距离是正常反作用力的杠杆臂。请注意，不需要按比例绘制矢量大小和杠杆臂，但必须清楚地标出所有相关量。

我们几乎准备好写下汽车的平衡条件方程\ ref {12.7} 到方程\ ref {12.9}，但首先我们必须决定参考框架。假设我们选择沿汽车长度的 x 轴，垂直的 y 轴，垂直于此 xy 平面的 z 轴。有了这个选择，我们只需要写方程\ ref {12.7} 和方程\ ref {12.9}，因为所有 y 分量都是相同的零。现在我们需要决定枢轴点的位置。我们可以选择任何点作为旋转轴（z 轴）的位置。假设我们将旋转轴放置在 CM 处，如汽车的自由车身图所示。此时，我们已经准备好写出汽车的平衡条件了。

解决方案

每个平衡条件仅包含三个项，因为有 N = 3 个力作用在汽车上。第一个平衡条件，方程\ ref {12.7}，显示为

\[+F_{F} - w + F_{R} = 0 \ldotp \label{12.11}\]

这个条件微不足道地得到满足，因为当我们替换数据时，方程\ ref {12.11} 变成 +0.52w − w + 0.48w = 0。第二个平衡条件，方程\ ref {12.9}，显示为

\[\tau_{F} + \tau_{w} + \tau_{R} = 0 \label{12.12}\]

其中\(\tau_{F}\)是力的扭矩 F _F，\(\tau_{w}\)是力 w 的重力扭矩，\(\tau_{R}\)是力的扭矩 F _R。当枢轴位于 CM 处时，重力扭矩等于零，因为重量相对于穿过 CM 的轴的杠杆臂为零。两种法向反作用力的作用线都垂直于它们的杠杆臂，因此在方程式\ ref {12.10} 中，两种力的作用线都有 |sin\(\theta\) | = 1。从自由体图中，我们看到，扭矩\(\tau_{F}\)导致在CM处绕枢轴顺时针旋转，因此其感应为负；扭矩\(\tau_{R}\)导致在CM处绕枢轴逆时针旋转，因此其感应为正。利用这些信息，我们将第二个均衡条件写为

\[-r_{F} F_{F} + r_{R} F_{R} = 0 \ldotp \label{12.13}\]

借助自由体图，我们确定了力大小 F _R = 0.48w 和 F _F = 0.52w，以及它们相应的杠杆臂 r _R = x 和 r _F = d − x。我们现在可以明确地写出第二个平衡条件，即方程\ ref {12.13}未知距离 x:

\[-0.52(d - x)w + 0.48xw = 0 \ldotp \label{12.14}\]

这里权重 w 取消，我们可以求解 CM 未知位置 x 的方程。答案是 x = 0.52d = 0.52 (2.5 m) = 1.3 m。解决方案在前轴位置选择枢轴不会改变结果。该枢轴位置的自由体图如图 12.6 所示。对于这种枢轴点的选择，第二个平衡条件是

\[-r_{w} w + r_{R} F_{R} = 0 \ldotp \label{12.15}\]

当我们替换图中所示的数量时，我们得到

\[-(d - x)w + 0.48dw = 0 \ldotp \label{12.16}\]

求解方程\ ref {12.13} 得到的答案再次是 x = 0.52d = 1.3 m。

图为示意图，显示轴距定义为 d 的乘用车的质量分布。该车 52% 的重量在前轮上，现在用圆圈标注并标有 Pivot (Ff)，48% 的重量放在平坦地面的后轮 (Fr) 上。后轴和质心之间的距离为 x。前轴和质心 (rw) 之间的距离为 d-x。整个轴的整个长度用方程 rr=D 标记。 — 图\(\PageIndex{5}\)：汽车的等效自由车身图；枢轴已清晰标明。

意义

这个例子表明，在求解静态平衡问题时，我们可以自由选择枢轴位置。对于轴心点的不同选择，我们有不同的平衡条件需要解决。但是，所有选择都会导致问题的相同解决方案。

练习 12.1

通过选择后轴位置的枢轴来求解示例 12.1。

练习 12.2

解释以下哪一种情况满足两种平衡条件：(a) 网球在空中移动时不旋转；(b) 在一个高度以恒定速度在空中滑行的鹈鹕；或 (c) 停放的汽车发动机的曲轴。

当物体上的所有外力作用在旋转轴上或沿着旋转轴起作用，或者可以忽略物体的空间延伸时，就会出现静态平衡的特殊情况。在这种情况下，可以有效地将物体当作点质量来对待。在这种特殊情况下，我们不必担心第二个平衡条件，即方程\ ref {12.9}，因为所有扭矩均为零，而第一个平衡条件（对于力）是唯一需要满足的条件。《牛顿运动定律和牛顿定律的应用》中概述了这个特殊案例的自由体图和问题解决策略。在下一个示例中，您将看到仅涉及第一个平衡条件的典型均衡情况。

观看此演示，看看三个砝码通过滑轮上的绳子连接在一起，打成一个结。你可以对权重进行实验，看看它们如何影响结的平衡位置，同时查看起作用的第一个平衡条件的矢量图表示。

示例 12.2：紧张情绪破裂

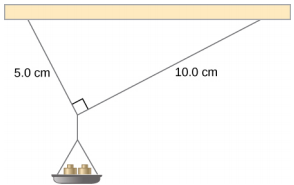
重量为 42.0 g 的小锅由两根绳子支撑，如图 12.7 所示。琴弦能承受的最大张力为 2.80 N。质量逐渐添加到锅中，直到其中一根琴弦折断。它是哪个字符串？必须增加多少质量才能发生这种情况？

图中显示了由两根以 90 度角相交的弦支撑的小质量平移。一根绳子的长度为 5 厘米，另一根绳子的长度为 10 厘米。 — 图\(\PageIndex{6}\)：质量逐渐添加到锅中，直到其中一根绳子折断。

策略

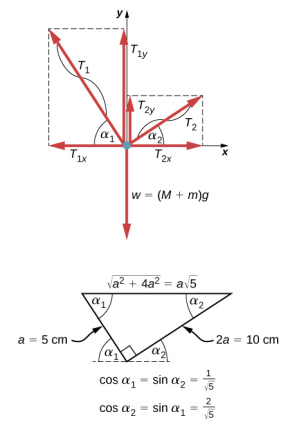
这种由琴弦、质量和平底锅组成的机械系统处于静态平衡状态。具体而言，将琴弦绑在锅上的结处于静态平衡状态。结可以视为一个点；因此，我们只需要第一个平衡条件。拉结的三种力量是 5.0 厘米绳子\(\vec{T}_{1}\)中的张力、10.0 厘米绳子\(\vec{T}_{2}\)中的张力以及容纳群众\(\vec{w}\)的平底锅的重量。我们采用矩形坐标系，y 轴指向与重力方向相反，然后绘制结的自由体图（见图 12.8）。要找到张力分量，我们必须确定方向角度\(\alpha_{2}\)，\(\alpha_{1}\)以及琴弦在水平方向（即 x 轴）上形成的方向角度。如图 12.7 所示，字符串构成直角三角形的两边。我们可以使用毕达哥拉斯定理来求解这个三角形，如图 12.8 所示，然后找到角度的正弦\(\alpha_{1}\)和余弦值\(\alpha_{2}\)。然后我们可以将张力解成它们的矩形分量，用第一个条件代替平衡（方程\ ref {12.7} 和方程\ ref {12.8}），然后求解字符串中的张力。张力较大的琴弦会先断裂。

上图显示了将琴弦绑在平底锅上的结的力的分布。 T1 和 T2 力量正在向上拉结。重量，M 和 m 的总和乘以 g 就是向下拉结。显示了 T1 和 T2 在 x 和 y 轴上的投影。下图显示了将琴弦绑在平底锅上的结表示为直角三角形。它的腿长度为 a 和 2a，a 等于 5 厘米。斜边是五的平方根。角度 alpha 1 由短腿和斜边形成。角度 alpha 2 由较长的腿和斜边形成。角度 alpha 1 的余弦等于角度 alpha 2 的正弦值，等于 1 除以五的平方根。角度 alpha 2 的余弦等于角度 alpha 1 的正弦值，等于 2 除以五的平方根。 — 图\(\PageIndex{7}\)：示例 12.2 中结的自由体图。

解决方案

w 拉结的重量是由于平底锅的质量 M 和添加到锅中的质量 m，或 w = (M + m) g。借助图 12.8 中的自由体图，我们可以为结设置平衡条件：

在 x 方向上，\[-T_{1x} + T_{2x} = 0\]在 y 方向上，\[+T_{1y} + T_{2y} - w = 0 \ldotp\]

从自由体图来看，这些方程中分量的大小为

\[\begin{split} T_{1x} & = T_{1} \cos \alpha_{1} = \frac{T_{1}}{\sqrt{5}},\quad T_{1y} = T_{1} \sin \alpha_{1} = \frac{2T_{1}}{\sqrt{5}} \\ T_{2x} & = T_{2} \cos \alpha_{2} = \frac{2T_{2}}{\sqrt{5}},\quad T_{2y} = T_{2} \sin \alpha_{2} = \frac{T_{2}}{\sqrt{5}} \ldotp \end{split}\]

我们将这些成分替换为平衡条件并进行简化。然后，我们得到两个张力的平衡方程：

在 x 方向上，\[T_{1} = 2T_{2}\]

在 y 方向上，\[\frac{2T_{1}}{\sqrt{5}} + \frac{T_{2}}{\sqrt{5}} = (M + m)g \ldotp\]

x 方向的平衡方程告诉我们，5.0 厘米弦中的张力 T ₁ 是 10.0 厘米弦中张力 T ₂ 的两倍。因此，较短的字符串会折断。当我们使用第一个方程从第二个方程中消除 T ₂ 时，我们得出了平底锅上的质量 m 与较短字符串中的张力 T ₁ 之间的关系：

\[\frac{2.5T_{1}}{\sqrt{5}} = (M + m)g \ldotp\]

当张力达到临界值 T ₁ = 2.80 N 时，弦断裂。对于断开弦的临界质量 m，上述方程可以求解：

\[m = \frac{2.5}{\sqrt{5}} \frac{T_{1}}{g} - M = \frac{2.5}{\sqrt{5}} \frac{2.80\; N}{9.8\; m/s^{2}} - 0.042\; kg = 0.277\; kg = 277.0\; g \ldotp\]

意义

假设本示例中考虑的机械系统安装在上升电梯内的天花板上。只要电梯以恒定速度向上移动，结果就会保持不变，因为重量 w 不会改变。如果升降机随着加速而向上移动，则临界质量会变小，因为升降机的加速会导致 M + m 的重量乘以明显的重量。尽管如此，在所有情况下，较短的字符串都会先断开。