10.6: 计算惯性矩
- Page ID
- 204760
- 计算形状均匀的刚体的惯性矩
- 应用平行轴定理找出与已知轴平行的任何轴的惯性矩
- 计算复合物体的惯性矩
在前面的小节中,我们定义了惯性矩,但没有说明如何计算。 在本小节中,我们将展示如何计算几种标准类型物体的惯性矩,以及如何使用已知的惯性矩来找到移动轴或复合物体的惯性矩。 本节对于了解如何将一般方程应用于复杂对象(这项技能对于更高级的物理和工程课程至关重要)非常有用。
惯性矩
我们将物体的惯性矩 I 定义为
\[I = \sum_{i} m_i r_i^2 \]
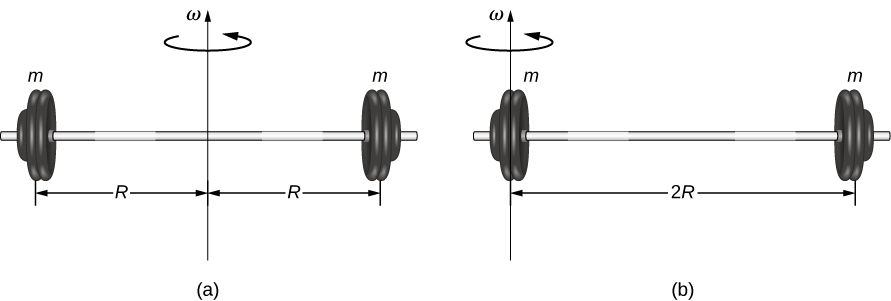
对于构成物体的所有点质量。 因为\(r\)是构成物体的每块质量块到旋转轴的距离,所以任何物体的惯性矩都取决于所选轴。 为了看这个,让我们举一个简单的例子,在无质量(质量可以忽略不计)杆的末端有两个质量(图\(\PageIndex{1}\)),然后计算两个不同轴的惯性矩。 在这种情况下,质量之和很简单,因为杠铃末端的两个质量可以近似为点质量,因此总和只有两个项。
在轴位于杠铃中心的情况下,两个质量 m 中的每一个都与轴线相距一段距\(R\)离,给出的惯性矩为
\[I_{1} = mR^{2} + mR^{2} = 2mR^{2} \ldotp\]
如果轴线位于杠铃末端(穿过其中一个质量),则惯性矩为
\[I_{2} = m(0)^{2} + m(2R)^{2} = 4mR^{2} \ldotp\]
从这个结果中,我们可以得出结论,旋转杠铃绕末端的难度是绕杠铃中心旋转的难度的两倍。
在这个例子中,我们有两个点质量,总和很容易计算。 但是,要处理不像点的物体,我们需要仔细考虑方程中的每个项。 该方程要求我们对每个 “质量块” 求和距旋转轴一定距离。 但是每个 “质量块” 到底是什么意思呢? 回想一下,在我们推导这个方程时,每块质量的速度大小相同,这意味着整个质量块与旋转轴必须有一个单一的距离 r。 但是,除非我们取一块无穷小的质量 dm,否则这是不可能的,如图所示\(\PageIndex{2}\)。
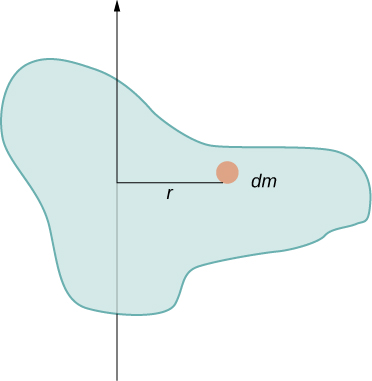
需要使用无穷小的质量块 dm,这表明我们可以通过计算无穷小质量上的积分来写出惯性矩,而不是对有限质量进行离散求和:
\[I = \sum_{i} m_{i} r_{i}^{2}\]
变成
\[I = \int r^{2} dm \ldotp \label{10.19}\]
实际上,这是我们概括复杂形状方程所需的形式。 最好详细地设计出具体的例子,以了解如何计算特定形状的惯性矩。 这是本节其余大部分内容的重点。
一根均匀的细杆,轴线穿过中心
假设质量为 M、长度为 L 的均匀(密度和形状)细棒,如图所示\(\PageIndex{3}\)。 我们想要一根细杆,这样我们就可以假设杆的横截面积很小,并且可以将杆视为沿着一维直线的一串质量。 在本示例中,为简单起见,旋转轴垂直于杆并穿过中点。 我们的任务是计算围绕该轴的惯性矩。 我们调整轴的方向,使 z 轴是旋转轴,而 x 轴穿过杆的长度,如图所示。 这是一个方便的选择,因为这样我们就可以沿 x 轴进行积分。
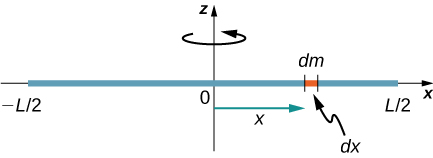
我们将 dm 定义为构成杆的一个小质量元素。 惯性矩积分是质量分布上的积分。 但是,我们知道如何在太空上进行整合,而不是在质量上进行整合。 因此,我们需要找到一种方法将质量与空间变量联系起来。 我们使用物体的线性质量密度\(\lambda\),即单位长度的质量。 由于这个物体的质量密度是均匀的,我们可以这样写
\[\lambda = \frac{m}{l}\; or\; m = \lambda l \ldotp\]
如果我们取这个方程两边的微分,我们会发现
\[dm = d(\lambda l) = \lambda (dl)\]
因为\(\lambda\)是常数。 为了方便起见,我们选择将杆沿着 x 轴定向,这正是这种选择变得非常有用的地方。 请注意,一根杆 dl 完全沿 x 轴放置,长度为 dx;实际上,在这种情况下,dl = dx。 因此,我们可以写 dm =\(\lambda\) (dx),给我们一个我们知道如何处理的积分变量。 每块质量 dm 与轴的距离由变量 x 给出,如图所示。 把这些放在一起,我们得到
\[I = \int r^{2} dm = \int x^{2} dm = \int x^{2} \lambda dx \ldotp\]
最后一步是要谨慎对待我们整合的局限性。 杆从 x = 延伸\(− \frac{L}{2}\)到 x =\(\frac{L}{2}\),因为轴位于杆的中间 x = 0。 这给了我们
\[\begin{split} I & = \int_{- \frac{L}{2}}^{\frac{L}{2}} x^{2} \lambda dx = \lambda \frac{x^{3}}{3} \Bigg|_{- \frac{L}{2}}^{\frac{L}{2}} \\ & = \lambda \left(\dfrac{1}{3}\right) \Bigg[ \left(\dfrac{L}{2}\right)^{3} - \left(- \dfrac{L}{2}\right)^{3} \Bigg] = \lambda \left(\dfrac{1}{3}\right) \left(\dfrac{L^{3}}{8}\right) (2) = \left(\dfrac{M}{L}\right) \left(\dfrac{1}{3}\right) \left(\dfrac{L^{3}}{8}\right) (2) \\ & = \frac{1}{12} ML^{2} \ldotp \end{split}\]
接下来,我们计算同一根均匀细杆的惯性矩,但轴选择不同,因此我们可以比较结果。 我们预计,围绕穿过质心的轴的惯性矩小于端点轴,就像本节开头的杠铃示例一样。 之所以发生这种情况,是因为更多的质量分布在离旋转轴更远的地方。
末端有轴的均匀细杆
现在考虑质量\(M\)和长度均匀的细杆\(L\),但是这次我们将旋转轴移动到杆的末端。 我们希望找到围绕这个新轴的惯性矩(图\(\PageIndex{4}\))。
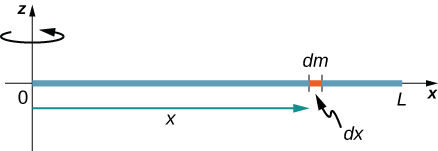
该\(dm\)量再次被定义为构成棒的一个小质量元素。 和以前一样,我们获得
\[I = \int r^{2} dm = \int x^{2} dm = \int x^{2} \lambda dx \ldotp\]
但是,这次我们对集成有不同的限制。 由于该轴位于杆的末端\(x = L\),因此杆从\(x = 0\)延伸到处\(x = 0\)。 因此,我们发现
\[\begin{align} I & = \int_{0}^{L} x^{2} \lambda\, dx \\[4pt] &= \lambda \frac{x^{3}}{3} \Bigg|_{0}^{L} \\[4pt] &=\lambda \left(\dfrac{1}{3}\right) \Big[(L)^{3} - (0)^{3} \Big] \\[4pt] & = \lambda \left(\dfrac{1}{3}\right) L^{3} = \left(\dfrac{M}{L}\right) \left(\dfrac{1}{3}\right) L^{3} \\[4pt] &= \frac{1}{3} ML^{2} \ldotp \label{ThinRod} \end{align} \]
请注意,杆绕其端点的旋转惯性比围绕其中心的旋转惯性(与杠铃示例一致)大四倍。
平行轴定理
找到杆绕轴线穿过中间的轴线和绕轴线穿过其末端的惯性矩的过程之间的相似之处令人震惊,这表明可能有一种更简单的方法来确定杆围绕平行于轴线的任何轴线穿过中心的惯性矩质量。 这样的轴称为平行轴。 这方面有一个定理,叫做平行轴定理,我们在此陈述了这个定理,但没有在本文中推导出来。
假设 m 是物体的质量,让 d 是从一个轴穿过物体质心到新轴的距离。 然后我们有
\[I_{\text{parallel-axis}} = I_{\text{center of mass}} + md^{2} \ldotp \label{10.20}\]
让我们将其应用于上面解析的带轴的均匀细杆示例:
\[I_{parallel-axis} = I_{center\; of\; mass} + md^{2} = \frac{1}{12} mL^{2} + m \left(\dfrac{L}{2}\right)^{2} = \left(\dfrac{1}{12} + \dfrac{1}{4}\right) mL^{2} = \frac{1}{3} mL^{2} \ldotp\]
这个结果与我们更长的计算(方程\ ref {ThinRod})一致。 方程\ ref {10.20} 是一个有用的方程式,我们在一些示例和问题中应用了这个方程。
如下图所示,半径\(R\)和质量\(m\)的圆柱体绕轴穿过曲面上的点的惯性矩是多少?
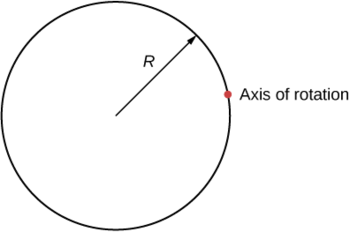
- 回答
-
\[I_{parallel-axis} = I_{center\; of\; mass} + md^{2} = mR^{2} + mR^{2} = 2mR^{2} \nonumber \]
围绕穿过中心的轴线形成统一的精简磁盘
积分以找出二维物体的惯性矩有点棘手,但是在这个研究层面上通常会形成一种形状,即围绕穿过其中心的轴线形成统一的薄盘(图\(\PageIndex{5}\))。
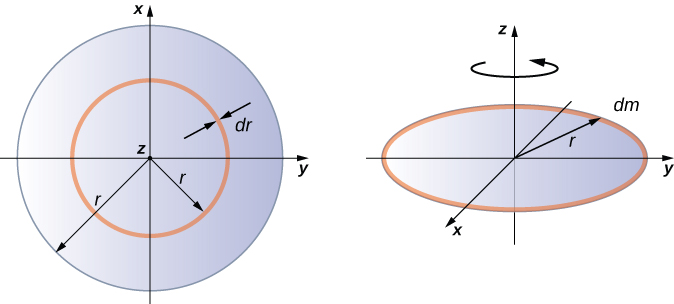
由于磁盘很薄,我们可以将质量完全分布在 xy 平面中。 我们再次从表面质量密度的关系开始,即单位表面积的质量。 由于表面质量密度均匀,因此表面质量密度\(\sigma\)是恒定的:
\[\sigma = \frac{m}{A}\]大概\[\sigma A = m\]是这样\[dm = \sigma (dA)\]
现在我们对该区域使用简化法。 可以将该区域视为由一系列细环组成,其中每个环是半径与轴\(r\)等距的质量增量 dm,如图 (b) 部分所示。 因此,每个环的无穷小面积由每个环\(dA\)的长度 (\(2 \pi r\)) 乘以每个环的无穷小宽度得出\(dr\):
\[A = \pi r^{2},\; dA = d(\pi r^{2}) = \pi dr^{2} = 2 \pi rdr \ldotp\]
然后,通过添加半径范围为到的所有细环\(0\)来构成磁盘的整个区域\(R\)。 然后,这个半径范围成为我们的积分极限\(dr\),也就是说,我们从\(r = 0\)到积分\(r = R\)。 把这些放在一起,我们有
\[\begin{split} I & = \int_{0}^{R} r^{2} \sigma (2 \pi r) dr = 2 \pi \sigma \int_{0}^{R} r^{3} dr = 2 \pi \sigma \frac{r^{4}}{4} \Big|_{0}^{R} \\ & = 2 \pi \sigma \left(\dfrac{R^{4}}{4} - 0 \right) = 2 \pi \left(\dfrac{m}{A}\right) \left(\dfrac{R^{4}}{4}\right) = 2 \pi \left(\dfrac{m}{\pi R^{2}}\right) \left(\dfrac{R^{4}}{4}\right) = \frac{1}{2} mR^{2} \ldotp \end{split}\]
请注意,这与图 10.5.4 中给出的值一致。
计算复合物体的惯性矩
现在考虑一个复合物体,比如图中的那个\(\PageIndex{6}\),它描绘了一根细棒末端的薄盘。 由于它不是一个形状均匀的物体,因此很难将其整合起来以找到惯性矩。 但是,如果我们回到最初的惯性矩定义为求和,我们可以推断出复合物体的惯性矩可以从物体每个部分的总和中得出:
\[I_{total} = \sum_{i} I_{i} \ldotp \label{10.21}\]
重要的是要注意,方程式中物体的惯性矩\(\PageIndex{6}\)是围绕公共轴的。 就这个物体而言,这将是一根长度为 L 的杆围绕其末端旋转,以及一个半径为的细圆盘围绕偏离中心一段距离的轴线\(R\)旋转\(L + R\),其中\(R\)是圆盘的半径。 让我们将杆的质量定义为 m r,将圆盘的质量定义为\(m_d\)。
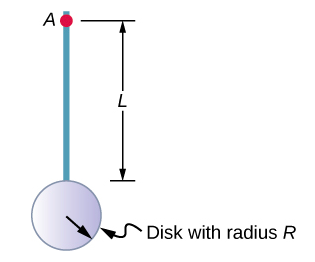
杆的惯性矩很简单\(\frac{1}{3} m_rL^2\),但我们必须使用平行轴定理来找到圆盘绕所示轴线的惯性矩。 圆盘围绕其中心的惯性矩是\(\frac{1}{2} m_dR^2\),我们应用平行轴定理(方程\ ref {10.20})来找出
\[I_{parallel-axis} = \frac{1}{2} m_{d} R^{2} + m_{d} (L + R)^{2} \ldotp\]
将杆的惯性矩加上旋转轴移位的圆盘惯性矩相加,我们发现复合物体的惯性矩为
\[I_{total} = \frac{1}{3} m_{r} L^{2} + \frac{1}{2} m_{d} R^{2} + m_{d} (L + R)^{2} \ldotp\]
应用惯性矩计算来解决问题
现在让我们来看看惯性矩计算的一些实际应用。
一个 25 公斤的孩子站在\(r = 1.0\, m\)距离旋转旋转木马轴线一段距离的地方(图\(\PageIndex{7}\))。 旋转木马可以近似为质量为 500 kg、半径为 2.0 m 的均匀实心圆盘。求出这个系统的惯性矩。
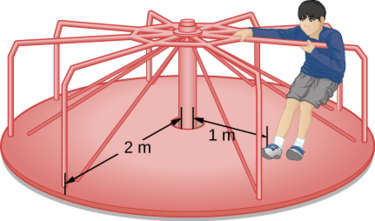
策略
这个问题涉及惯性矩的计算。 我们得到了孩子旋转轴的质量和距离,以及旋转木马的质量和半径。 由于孩子的质量和大小比旋转木马小得多,我们可以将孩子近似为点质量。 我们使用的表示法是 m c = 25 kg,r c = 1.0 m,m m = 500 kg,r m = 2.0 m。我们的目标是找出\(I_{total} = \sum_{i} I_{i}\)(方程\ ref {10.21})。
解决方案
为了孩子\(I_c = m_cr^2\),为了旋转木马,\(I_m = \frac{1}{2}m_m r^2\)。 因此
\[I_{total} = 25(1)^{2} + \frac{1}{2} (500)(2)^{2} = 25 + 1000 = 1025\; kg\; \cdotp m^{2} \ldotp \nonumber \]
意义
该值应接近旋转木马本身的惯性矩,因为旋转木马远离轴线的质量比子旋转木马的质量要大得多。
求出杆和实心球体组合围绕两个轴的惯性矩,如下所示。 鱼竿的长度为 0.5 米,重量为 2.0 千克。 球体的半径为 20.0 厘米,质量为 1.0 千克。
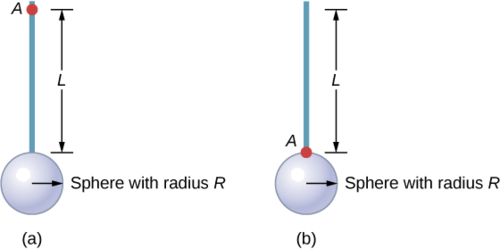
策略
由于在这两种情况下我们都有一个复合对象,因此我们可以使用平行轴定理来找出每个轴的惯性矩。 在 (a) 中,球体的质心位于距离旋转轴一定\(L + R\)距离处。 在 (b) 中,球体的质心位于\(R\)距离旋转轴一定距离的位置。 在这两种情况下,杆的惯性矩都围绕一端的轴线。 有关各个物体的惯性矩,请参阅表 10.4。
一个。
\[\begin{split} I_{total} & = \sum_{i} I_{i} = I_{Rod} + I_{Sphere}; \\ I_{Sphere} & = I_{center\; of\; mass} + m_{Sphere} (L + R)^{2} = \frac{2}{5} m_{Sphere} R^{2} + m_{Sphere} (L + R)^{2}; \\ I_{total} & = I_{Rod} + I_{Sphere} = \frac{1}{3} m_{Rod} L^{2} + \frac{2}{5} m_{Sphere} R^{2} + m_{Sphere} (L + R)^{2}; \\ I_{total} & = \frac{1}{3} (20\; kg)(0.5\; m)^{2} + \frac{2}{5} (1.0\; kg)(0.2\; m)^{2} + (1.0\; kg)(0.5\; m + 0.2\; m)^{2}; \\ I_{total} & = (0.167 + 0.016 + 0.490)\; kg\; \cdotp m^{2} = 0.673\; kg\; \cdotp m^{2} \ldotp \end{split}\]
b。
\[\begin{split} I_{Sphere} & = \frac{2}{5} m_{Sphere} R^{2} + m_{Sphere} R^{2}; \\ I_{total} & = I_{Rod} + I_{Sphere} = \frac{1}{3} m_{Rod} L^{2} + \frac{2}{5} (1.0\; kg)(0.2\; m)^{2} + (1.0\; kg)(0.2\; m)^{2}; \\ I_{total} & = (0.167 + 0.016 + 0.04)\; kg\; \cdotp m^{2} = 0.223\; kg\; \cdotp m^{2} \ldotp \end{split}\]
意义
使用平行轴定理可以简化复合物体惯性矩的计算。 我们看到 (a) 中的惯性矩大于 (b)。 这是因为旋转轴更接近 (b) 中系统的质心。 一个简单的类比就是一根棒。 一端的惯性矩为\(\frac{1}{3}\) mL 2,但沿其长度穿过质心的惯性矩为\(\frac{1}{12}\) mL 2。
杆状的摆锤以 30° 的角度脱离静止状态(图\(\PageIndex{8}\))。 它的长度为 30 cm,质量为 300 g。它的最低点的角速度是多少?
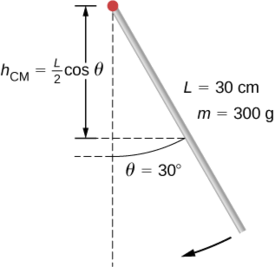
策略
使用节能来解决问题。 在释放点,钟摆具有引力势能,这是根据质心在摆动中最低点以上的高度确定的。 在秋千的底部,所有的引力势能都转化为旋转动能。
解决方案
势能的变化等于旋转动能的变化\(\Delta U + \Delta K = 0\)。
在秋千的顶部:
\[U = mgh_{cm} = mgL^2 (\cos \theta). \nonumber \]
在秋千的底部,
\[U = mg \frac{L}{2}. \nonumber\]
在挥杆顶部,旋转动能为 K = 0。 在秋千的底部,K =\(\frac{1}{2} I \omega^{2}\)。 因此:
\[\Delta U + \Delta K = 0 \Rightarrow (mg \frac{L}{2} (1 - \cos \theta) - 0) + (0 - \frac{1}{2} I \omega^{2}) = 0 \nonumber\]
要么
\[\frac{1}{2} I \omega^{2} = mg \frac{L}{2} (1 - \cos \theta) \ldotp \nonumber\]
求解\(\omega\),我们有
\[\omega = \sqrt{mg \frac{L}{I} (1 - \cos \theta)} = \sqrt{mg \frac{L}{\frac{1}{3} mL^{2}} (1 - \cos \theta)} = \sqrt{g \frac{3}{L} (1 - \cos \theta)} \ldotp \nonumber\]
插入数值,我们有
\[\omega = \sqrt{(9.8\; m/s^{2}) \left(\dfrac{3}{0.3\; m}\right) (1 - \cos 30)} = 3.6\; rad/s \ldotp \nonumber\]
意义
请注意,摆锤的角速度不取决于其质量。


