10.5: 惯性矩和旋转动能
- Page ID
- 204728
- 描述旋转动能和平移动能之间的区别
- 根据旋转轴的质量分布定义惯性矩的物理概念
- 解释刚体的惯性矩如何影响其旋转动能
- 利用机械能守恒来分析同时处于旋转和平移状态的系统
- 当非保守力量导致能量损失时,计算旋转系统的角速度
到目前为止,在本章中,我们一直在研究旋转运动学:描述具有固定旋转轴的旋转刚体的运动。 在本节中,我们定义了两个有助于分析旋转物体特性的新量:惯性矩和旋转动能。 定义了这些属性后,我们将拥有分析旋转动力学所需的两个重要工具。
旋转动能
任何移动的物体都有动能。 我们知道如何计算正在进行平移运动的物体的这个值,但是对于正在旋转的刚体来说,怎么样呢? 这可能看起来很复杂,因为刚体上的每个点都有不同的速度。 但是,我们可以利用角速度(对整个刚体来说是相同的)来表示旋转物体的动能。 该图\(\PageIndex{1}\)显示了一个非常有活力的旋转体的示例:由马达推动的电动磨石。 火花飞扬,磨石工作时会产生噪音和振动。 该系统具有可观的能量,其中一些以热、光、声音和振动的形式出现。 但是,这些能量中的大部分是旋转动能的形式。
旋转运动中的能量不是一种新的能量形式;相反,它是与旋转运动相关的能量,与平移运动中的动能相同。 但是,由于动能由给出\(K=\frac{1}{2}mv^2\),而速度是旋转物体上绕轴线上每个点的不同量,因此找到一种用变量写动能的方法是有意义的\(\omega\),刚性旋转体上的所有点都是相同的。 对于绕固定轴旋转的单个粒子,计算起来很简单。 我们可以使用关系将角速度与平移速度的大小联系起来\(v_t=\omega r\),其中\(r\)是粒子与旋转轴的距离,\(v_t\)是其切向速度。 用动能方程代替,我们发现
\[ K=\frac{1}{2} m v_{t}^{2}=\frac{1}{2} m(\omega r)^{2}=\frac{1}{2}\left(m r^{2}\right) \omega^{2}. \nonumber \]
对于刚性旋转体,我们可以将任何物体分成大量较小的质量,每个质量都有质量\(m_j\)和与旋转轴的距离\(r_j\),这样物体的总质量等于单个质量的总和:\(M=\sum_{j} m_{j}\)。 每个较小的质量都有切线速度\(v_j\),我们暂时取消了下标\(t\)。 刚性旋转体的总动能为
\[ K=\sum_{j} \frac{1}{2} m_{j} v_{j}^{2}=\sum_{j} \frac{1}{2} m_{j}\left(r_{j} \omega_{j}\right)^{2} \nonumber \]
因为\(\omega_j = \omega\)对于所有群众来说,
\[ K=\frac{1}{2}\left(\sum_{j} m_{j} r_{j}^{2}\right) \omega^{2} . \label{10.16} \]
方程\ ref {10.16} 的单位是焦耳 (J)。 这种形式的方程式很完整,但很尴尬;我们需要找到一种方法来概括它。
惯性矩
如果我们将方程\ ref {10.16} 与在 Wor k and Kinetic Energy (\(\frac{1}{2}mv^2\)) 中写动能的方式进行比较,这表明我们有一个新的旋转变量要添加到旋转变量和平移变量之间的关系列表中。 该量\(\sum_{j} m_{j} r_{j}^{2}\)是旋转动能方程中质量的对应物。 这是旋转运动的一个重要新术语。 这个量称为惯性矩\(I\),单位为 kg·m 2:
\[ I=\sum_{j} m_{j} r_{j}^{2} . \label{10.17} \]
现在,我们将表达式保留为求和形式,表示绕固定轴旋转的点粒子系统的惯性矩。 我们注意到,单点粒子绕固定轴的惯性矩很简单\(mr^2\),\(r\)就是从点粒子到旋转轴的距离。 在下一节中,我们将探讨这个方程的积分形式,它可以用来计算一些规则形状的刚体的惯性矩。
惯性矩是旋转惯性的定量测量,就像在平移运动中一样,质量是线性惯性的定量度量,也就是说,物体越大,它的惯性就越大,它对线性速度变化的阻力就越大。 同样,刚体或粒子系统的惯性矩越大,它对绕固定旋转轴的角速度变化的阻力就越大。 有趣的是,在方程式\ ref {10.17} 中,看到惯性矩如何随着 r(质量粒子到旋转轴的距离)而变化。 刚体和质量较大的粒子系统集中在距离旋转轴更远的距离上,其惯性矩比相同质量的物体和系统具有更大的惯性矩,但集中在旋转轴附近。 通过这种方式,我们可以看到,当绕轴线旋转穿过中心时,空心圆柱体比相同质量的实心圆柱体具有更大的旋转惯性。 用方程\ ref {10.17} 代入方程\ ref {10.16},旋转刚体动能的表达式变成
\[ K=\frac{1}{2} I \omega^{2} . \label{10.18} \]
从这个方程中我们可以看出,旋转刚体的动能与惯性矩和角速度的平方成正比。 飞轮储能设备利用了这一点,飞轮储能设备旨在存储大量的旋转动能。 许多汽车制造商现在正在测试汽车中的飞轮储能设备,例如飞轮或动能回收系统,如图所示\(\PageIndex{2}\)。

表 10.4 总结了动能和惯性的旋转和平移量。 不包括关系列,因为不存在常量,我们可以将旋转量乘以得到平移量,就像表 10.3 中的变量一样。
| 轮换 | 翻译的 |
|---|---|
| \(I=\sum_{j} m_{j} r_{j}^{2}\) | \(m\) |
| \(K = \frac{1}{2}I \omega^2\) | \(K = \frac{1}{2} m v^2 \) |
六个小垫圈间隔 10 厘米,在一根质量可以忽略不计、长 0.5 米的杆上。 每个垫圈的质量为 20 g。杆绕位于 25 cm 处的轴旋转,如图所示\(\PageIndex{3}\)。 (a) 系统的惯性矩是多少? (b) 如果拆下最靠近轴线的两个垫圈,剩下的四个垫圈的惯性矩是多少? (c) 如果有六个垫圈的系统以 5 转/秒的速度旋转,那么它的旋转动能是多少?
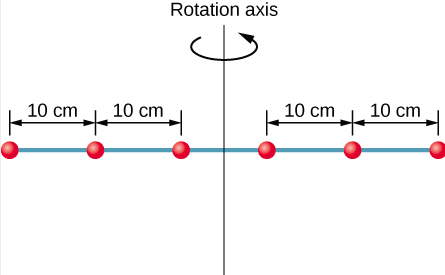
策略
- 我们使用粒子系统的惯性矩的定义,并通过求和来计算该量。 质量都是一样的,所以我们可以把这个数量拉到求和符号的前面。
- 我们做了类似的计算。
- 我们将来自 (a) 的结果插入到旋转动能的表达式中。
解决方案
- \(I=\sum m_{j} r_{j}^{2}=(0.02 \: \mathrm{kg})\left(2 \times(0.25 \: \mathrm{m})^{2}+2 \times(0.15 \: \mathrm{m})^{2}+2 \times(0.05 \: \mathrm{m})^{2}\right)=0.0035 \: \mathrm{kg} \cdot \mathrm{m}^{2}\)
- \(I=\sum_{j} m_{j} r_{j}^{2}=(0.02 \: \mathrm{kg})\left(2 \times(0.25 \: \mathrm{m})^{2}+2 \times(0.15 \: \mathrm{m})^{2}\right)=0.0034 \: \mathrm{kg} \cdot \mathrm{m}^{2}\)
- \(K=\frac{1}{2} I \omega^{2}=\frac{1}{2}\left(0.0035 \: \mathrm{kg} \cdot \mathrm{m}^{2}\right)(5.0 \times 2 \pi \: \mathrm{rad} / \mathrm{s})^{2}=1.73 \: \mathrm{J}\)
意义
我们可以看到个人对惯性矩的贡献。 靠近旋转轴的质量的贡献很小。 当我们移除它们时,它对惯性矩的影响很小。
在下一节中,我们将概括点粒子的求和方程,并开发一种计算刚体惯性矩的方法。 但是,就目前而言,Figure\(\PageIndex{4}\) 给出了围绕指定轴的常见物体形状的旋转惯性值。
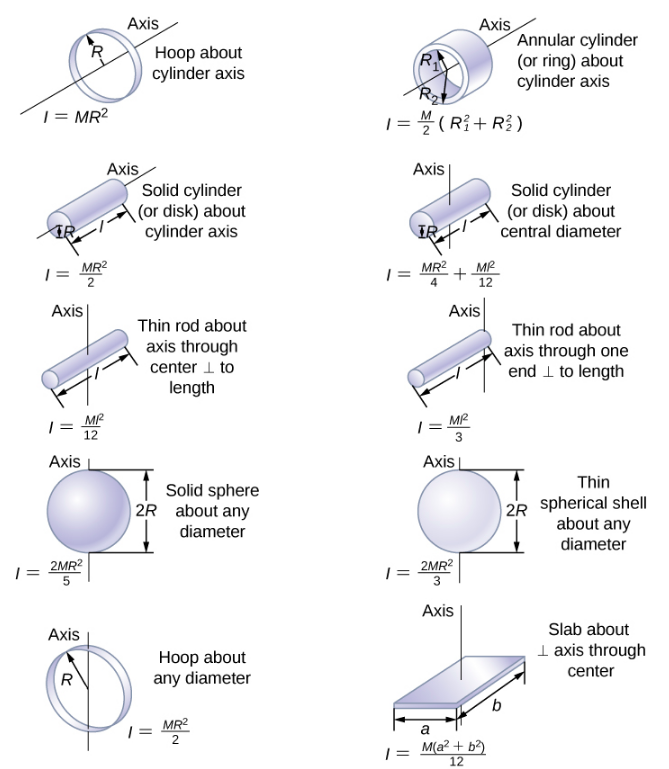
应用旋转动能
现在,让我们运用旋转动能和惯性矩表的概念,来感受与几个旋转物体相关的能量。 以下示例还将帮助您熟悉使用这些方程式。 首先,让我们看一下旋转能量的一般问题解决策略。
- 确定轮换中涉及能量或工作。
- 确定感兴趣的系统。 草图通常会有所帮助。
- 分析情况以确定所涉及的工作类型和精力。
- 如果没有由于摩擦和其他非保守力量而造成的能量损失,则机械能是守恒的,也就是说\(K_i + U_i = K_f + U_f\)。
- 如果存在非保守力量,则机械能不守恒,其他形式的能量,例如热和光,可能会进入或离开系统。 确定它们是什么并在必要时进行计算。
- 尽可能删除术语以简化代数。
- 评估数值解,看看它在问题措辞中呈现的物理环境中是否有意义。
一架典型的小型救援直升机有四个叶片:每个叶片长 4.00 m,重量为 50.0 kg(图\(\PageIndex{5}\))。 叶片可以近似为细棒,围绕垂直于其长度的轴的一端旋转。 直升机的总装载质量为 1000 千克。 (a) 计算叶片以 300 rpm 旋转时的旋转动能。 (b) 计算直升机以 20.0 m/s 飞行时的平移动能,并将其与叶片中的旋转能量进行比较。

策略
旋转动能和平移动能可以根据它们的定义来计算。 问题的措辞为计算旋转和平移动能的表达式提供了所有必要的常数。
解决方案
a. 旋转动能是
\[ K = \frac{1}{2} I \omega^2 \nonumber \]
我们必须将角速度转换为每秒弧度并计算惯性矩,然后才能找到\(K\)。 角速度\(\omega\)为
\[ \omega=\frac{300 \text { rev }}{1.00 \min } \frac{2 \pi \text { rad }}{1 \text { rev }} \frac{1.00 \: \min }{60.0 \: \mathrm{s}}=31.4 \: \frac{\mathrm{rad}}{\mathrm{s}}. \nonumber \]
一把刀片的惯性矩是一根细杆绕其末端旋转的惯性矩,如图所示\(\PageIndex{4}\)。 总数\(I\)是这个惯性矩的四倍,因为有四个刀片。 因此,
\[ I=4 \frac{M l^{2}}{3}=4 \times \frac{(50.0 \: \mathrm{kg})(4.00 \: \mathrm{m})^{2}}{3}=1067.0 \: \mathrm{kg} \cdot \mathrm{m}^{2} \nonumber .\]
输入\(\omega\)和\(I\)进入旋转动能的表达式得出
\[ K=0.5\left(1067 \: \mathrm{kg} \cdot \mathrm{m}^{2}\right)(31.4 \: \mathrm{rad} / \mathrm{s})^{2}=5.26 \times 10^{5} \: \mathrm{J}. \nonumber \]
b. 将给定值输入平移动能方程中,我们得到
\[ K=\frac{1}{2} m v^{2}=(0.5)(1000.0 \: \mathrm{kg})(20.0 \: \mathrm{m} / \mathrm{s})^{2}=2.00 \times 10^{5} \: \mathrm{J} . \nonumber \]
为了比较动能,我们采用平移动能与旋转动能的比率。 这个比率是
\[ \frac{2.00 \times 10^{5} \: \mathrm{J}}{5.26 \times 10^{5} \: \mathrm{J}}=0.380 . \nonumber \]
意义
平移能量与旋转动能之比仅为 0.380。 这个比率告诉我们,直升机的大部分动能来自其旋转的叶片。
一个人以30.0 m/s的速度向空中投掷回旋镖,相对于水平方向成40.0°的角度(图\(\PageIndex{6}\))。 它的质量为 1.0 kg,以 10.0 rev/s 的速度旋转。回旋镖的惯性矩计算为\(I=\frac{1}{12} m L^{2} \) where\(L\) = 0.7 m。(a) 回旋镖离开手牌时的总能量是多少? (b) 忽略空气阻力,回旋镖从手的抬高处起有多高?
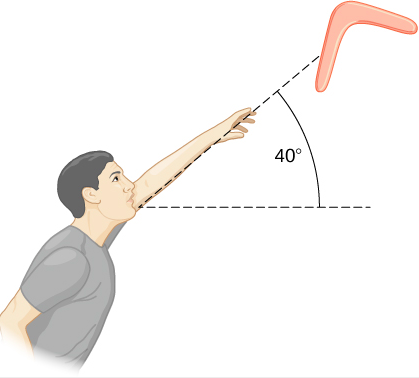
策略
我们使用旋转动能和线性动能的定义来计算系统的总能量。 问题在于忽视空气阻力,因此我们不必担心能量损失。 在(b)部分中,我们使用机械能守恒来找出回旋镖的最大高度。
解决方案
a. 惯性矩:\( I=\frac{1}{12} m L^{2}=\frac{1}{12}(1.0 \: \mathrm{kg})(0.7 \: \mathrm{m})^{2}=0.041 \: \mathrm{kg} \cdot \mathrm{m}^{2}. \)
角速度:\( \omega=(10.0 \: \mathrm{rev} / \mathrm{s})(2 \pi)=62.83 \: \mathrm{rad} / \mathrm{s} \)
因此,旋转动能是
\[ K_{R}=\frac{1}{2}\left(0.041 \: \mathrm{kg} \cdot \mathrm{m}^{2}\right)(62.83 \: \mathrm{rad} / \mathrm{s})^{2}=80.93 \: \mathrm{J} \nonumber \]
平移动能是
\[ K_{\mathrm{T}}=\frac{1}{2} m v^{2}=\frac{1}{2}(1.0 \: \mathrm{kg})(30.0 \: \mathrm{m} / \mathrm{s})^{2}=450.0 \: \mathrm{J} \nonumber \]
因此,回旋镖中的总能量为
\[ K_{\text {Total }}=K_{R}+K_{T}=80.93+450.0=530.93 \: \mathrm{J}. \nonumber \]
b. 我们使用机械能守恒。 由于回旋镖是以一定角度发射的,因此我们需要使用 x 和 y 方向的速度用其线性动能来写出系统的总能量。 回旋镖离开手牌时的总能量为
\[ E_{\text {Before }}=\frac{1}{2} m v_{x}^{2}+\frac{1}{2} m v_{y}^{2}+\frac{1}{2} I \omega^{2} \nonumber \]
最大高度处的总能量为
\[ E_{\text {Final }}=\frac{1}{2} m v_{x}^{2}+\frac{1}{2} I \omega^{2}+m g h \nonumber \]
通过守恒机械能,\(E_{Before} = E_{Final}\)所以在取消类似的条款之后,
\[ \frac{1}{2} m v_{y}^{2}=m g h \nonumber .\]
由于\(v_y\) = 30.0 m/s (\(\sin 40^{\circ}\)) = 19.28 m/s,我们发现
\[ h=\frac{(19.28 \: \mathrm{m} / \mathrm{s})^{2}}{2\left(9.8 \: \mathrm{m} / \mathrm{s}^{2}\right)}=18.97 \: \mathrm{m} \nonumber \]
意义
在 (b) 部分中,解决方案演示了节能是解决通常使用运动学解决的问题的替代方法。 在没有空气阻力的情况下,旋转动能不是求解最大高度的一个因素。
核潜艇螺旋桨的惯性矩为 800.0 kg • m 2。 如果潜水螺旋桨在发动机被切断时旋转速度为 4.0 rev/s,那么当水阻力消耗了 50,000 J 时,螺旋桨在 5.0 秒后的旋转速度是多少?


