7.4: 工作能量定理
- Page ID
- 204875
- 考虑到作用在粒子上的力,应用工作能量定理来查找有关粒子运动的信息
- 使用工作能量定理查找有关作用在粒子上的力的信息,前提是有关粒子运动的信息
我们已经讨论了如何找到作用在粒子上的力对粒子所做的工作,但是这种工作如何体现在粒子的运动中? 根据牛顿的第二运动定律,作用于粒子的所有力或净力的总和决定了粒子动量或其运动的变化速率。 因此,我们应该考虑作用于粒子的所有力或网络所做的工作,以了解它对粒子的运动产生了什么影响。
让我们先来看看粒子在无穷小位移上移动时对粒子所做的网络工作,该位移是净力和位移的点积:
\[dW_{net} = \vec{F}_{net} \cdotp d \vec{r}. \nonumber\]
牛顿第二定律告诉我们
\[\vec{F}_{net} = m \left(\dfrac{d \vec{v}}{dt}\right) \nonumber\]
所以
\[dW_{net} = m \left(\dfrac{d \vec{v}}{dt}\right) \cdotp d \vec{r}. \nonumber\]
对于描述物理粒子运动的数学函数,我们可以将微分 dt 等重新排列为这个表达式中的代数量,也就是说,
\[\begin{align*} dW_{net} &= m \left(\dfrac{d \vec{v}}{dt}\right) \cdotp d \vec{r} \\[4pt] &= m\, d \vec{v}\; \cdotp \left(\dfrac{d \vec{r}}{dt}\right) \\[4pt] &= m \vec{v}\; \cdotp d \vec{v}, \end{align*}\]
在这里,我们用速度代替了位移的时间导数,并使用了点积的交换特性。 由于此时您可能更熟悉标量的导数和积分,因此在对粒子轨迹上的任意两个点 A 和 B 进行积分之前,我们使用笛卡尔坐标来表示点积。 这为我们提供了在粒子上完成的网络工作:
\[\begin{align} W_{net,\; AB} & = \int_{A}^{B} (mv_{x} dv_{x} + mv_{y}dv_{y} + mv_{z}dv_{z} \\[4pt] & = \frac{1}{2} m \left| v_{x}^{2} + v_{y}^{2} + v_{z}^{2} \right|_{A}^{B} = \left|\frac{1}{2} mv^{2} \right|_{A}^{B} = K_{B} - K_{A} \ldotp \end{align} \label{7.8}\]
在中间步骤中,我们使用了速度的平方是其笛卡尔分量的平方和这一事实,在最后一步中,我们使用了粒子动能的定义。 这个重要的结果被称为工作能量定理。
对粒子所做的净功等于粒子动能的变化:
\[W_{net} = K_{B} - K_{A} \ldotp \label{7.9}\]

根据这个定理,当一个物体减速时,它的最终动能小于其初始动能,其动能的变化是负的,对其进行的网络工作也是如此。 如果物体加速,则对其完成的网络工作量为正值。 计算网络时,必须包括作用于物体的所有力。 如果你遗漏任何作用于物体的力,或者如果你包括任何不作用于物体的力,你就会得到错误的结果。
工作能量定理的重要性及其引发的进一步概括在于,它使某些类型的计算比试图解开牛顿第二定律要容易得多。 例如,在牛顿运动定律一节中,我们通过求解牛顿第二加速度定律并使用运动学方程求出恒定加速度,得出物体在无摩擦平面上滑动的速度
\[v_{f}^{2} = v_{i}^{2} + 2g(s_{f} - s_{i}) \sin \theta,\]
飞机下方的\(s\)位移在哪里。
我们也可以从工作能量定理(方程\ ref {7.9})中得到这个结果。 由于只有两种力作用在物体上:重力和法向力,而法向力不起任何作用,因此网络作用只是由重力完成的工作。 这仅取决于物体的重量和高度的差异,所以
\[W_{net} = W_{grav} = -mg (y_{f} - y_{i}),\]
哪里\(y\)是正向上。 工作能量定理说这等于动能的变化:
\[-mg (y_{f} - y_{i}) = \frac{1}{2} (v_{f}^{2} - v_{i}^{2}) \ldotp\]
使用直角三角形,我们可以看出
\[(y_f − y_i) = (s_f − s-i)\sin \theta, \nonumber\]
所以最终速度的结果是一样的。
使用工作能量定理可以获得什么? 答案是,对于无摩擦的飞机表面来说,并不多。 但是,只有在这种特殊情况下,牛顿的第二定律才容易求解,而工作能量定理给出了任何形状的无摩擦表面的最终速度。 对于任意曲面,法向力不是恒定的,牛顿第二定律可能难以或不可能通过分析求解。 不管是否恒定,对于沿曲面的运动,法向力永远不起作用,因为它垂直于位移。 使用工作能量定理进行计算可以避免这种困难,适用于更一般的情况。
- 为物体上的每种力绘制自由体图。
- 确定每种力是否对图中的位移起作用。 一定要在已完成的工作中保留任何正面或负面的信号。
- 将每支部队完成的总工作量相加。
- 将此总功率设置为等于动能的变化,然后求解任何未知参数。
- 检查你的答案。 如果物体以恒定速度或零加速度行驶,则完成的总功率应为零,并与动能的变化相匹配。 如果总功率为正,则物体必须加速或增加动能。 如果总功率为负,则物体的动能必须减慢或降低
玩具车的无摩擦轨道包括半径循环\(R\)。 从回路底部测量,必须将赛车放置在多高处,才能在接近的轨道上从静止处开始,然后一直绕着环路行驶?
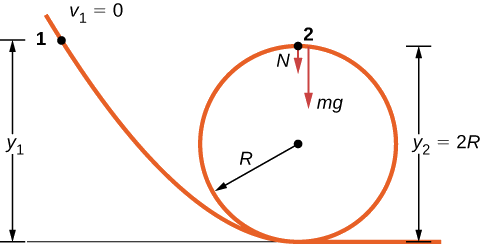
策略
物体最终位置的自由体图绘制在图中\(\PageIndex{2}\)。 引力工作是针对位移所做的唯一不为零的工作。 由于权重指向的方向与净垂直位移的方向相同,因此引力所做的总功率为正。 根据工作能量定理,起始高度决定了环路顶部的汽车的速度,
\[mg(y_{2} - y_{1}) = \dfrac{1}{2} mv_{2}^{2}, \nonumber\]
其中的符号显示在随附的图中。 在循环的顶部,法向力和重力都向下,加速度是向心的,所以
\[a_{top} = \dfrac{F}{m} = \dfrac{N + mg}{m} = \frac{v_{2}^{2}}{R} \ldotp \nonumber\]
与轨道保持接触的条件是,无论多么微小,都必须有一定的法力;也就是说\(N > 0\)。 用 and\(v_{2}^{2}\) 代替 and\(N\),我们可以找到条件\(y_1\)。
解决方案
实施策略中的步骤以达到预期的结果:
\[N = -mg + \frac{mv_{2}^{2}}{R} = \frac{-mgR + 2mg(y_{1} - 2R)}{R} > 0\; or\; y_{1} > \frac{5R}{2} \ldotp \nonumber\]
意义
在回路表面,重力的法向分量和法向接触力必须提供汽车绕环行驶的向心加速度。 重力的切向分量使汽车减速或加速。 通过反复试验,孩子会发现启动汽车需要多高,但是既然你知道了工作能量定理,你可以根据物理原理预测最小高度(以及其他更有用的结果)。 通过使用工作能量定理,你不必求解微分方程来确定高度。
假设示例中 loop-the-loop 的半径\(\PageIndex{1}\)为 15 cm,玩具车在距离底部 45 cm 的高度从静止处开始。 它在循环顶端的速度是多少?
在物体的运动已知但作用于其上的一个或多个力的值未知的情况下,你可以使用工作能定理来获取有关力的一些信息。 工作取决于其作用的力量和距离,因此信息是通过他们的产品提供的。
子弹的质量为 40 颗粒(2.60 g),枪口速度为 1100 英尺。 /s (335 m/s)。 它可以穿透八块 1 英寸的松木板,每块厚度为 0.75 英寸。 木材施加的平均制动力是多少,如图所示\(\PageIndex{3}\)?
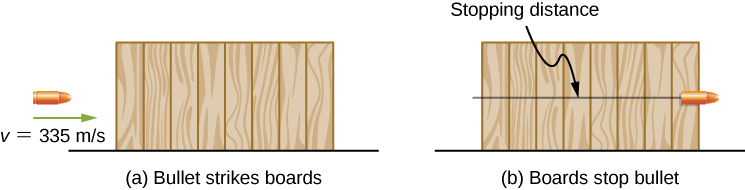
策略
我们可以假设,在上述一般条件下,子弹会失去穿透板的所有动能,因此工作能定理说其初始动能等于平均制动力乘以穿透距离。 子弹动能的变化和阻止子弹的网络功率都是负的,所以当你写出工作能量定理时,网络功率等于平均力乘以停止距离,这就是你得到的。 子弹穿透的八块 1 英寸松木板的总厚度为 8 x\(\frac{3}{4}\) 英寸 = 6 英寸 = 15.2 厘米。
解决方案
运用工作能量定理,我们得到
\[W_{net} = - F_{ave} \Delta s_{stop} = - K_{initial} , \nonumber\]
所以
\[F_{ave} = \frac{\frac{1}{2} mv^{2}}{\Delta s_{stop}} = \frac{\frac{1}{2} (2.66 \times 10^{-3}\; kg)(335\; m/s)^{2}}{0.152\; m} = 960\; N \ldotp \nonumber\]
意义
我们本可以在这个例子中使用牛顿第二定律和运动学,但是工作能量定理也为不太简单的情况提供了答案。 阿西夫·沙库尔最近的文章 [“Bullet-Block Science Video Puzzle”)的一节讨论了子弹垂直向上发射到一块木块中的穿透力。 物理老师(2015 年 1 月)53 (1):15-16]。 如果子弹在死点处射入方块,它会失去所有动能,穿透距离比偏离中心发射时稍远一些。 原因是,如果子弹击中偏离中心,它停止穿透后会有一点动能,因为方块会旋转。 工作能定理意味着动能变化越小,穿透力越小。 在你读完 Angular Momentum 之后,你将在这篇有趣的文章中更多地了解物理学。
在这个名为 “坡道” 的 PhET 模拟 (https://phet.colorado.edu/en/simulation/the-ramp) 中了解有关工作和能量的更多信息。 尝试改变推动箱子的力和沿斜坡的摩擦力。 可以查看功率图和能量图,记录已完成的总功率和箱体动能的变化。


