6.5:摩擦(第 2 部分)
- Page ID
- 204984
摩擦和倾斜面
摩擦起着明显作用的一种情况是斜坡上的物体。 可能是板条箱被推上坡道到装卸码头,或者是滑板手滑下山了,但基本的物理原理是一样的。 我们通常将倾斜的表面概括起来,称之为倾斜的平面,但随后假装表面是平坦的。 让我们来看一个分析带有摩擦力的倾斜平面上的运动的示例。
重量为62 kg的滑雪者正在以恒定速度滑下白雪皑皑的斜坡。 如果已知摩擦力为 45.0 N,则求出滑雪者的动摩擦系数
策略
动摩擦的大小为 45.0 N。动摩擦力与法向力 N 相关 f k =\(\mu_{k}\) N;因此,如果我们能找到滑雪者的法向力,我们就能找到动摩擦系数。 法向力始终垂直于表面,并且由于没有垂直于地表的运动,因此法向力应等于滑雪者垂直于斜坡的体重分量。 (参见图\(\PageIndex{1}\),它重复了牛顿运动定律一章中的一个数字。)
我们有
\[N = w_{y} = w \cos 25^{o} = mg \cos 25^{o} \ldotp\]
用它代替我们的动摩擦表达式,我们得到
\[f_{k} = \mu_{k} mg \cos 25^{o},\]
现在可以求解动摩擦系数\(\mu_{k}\)。
解决方案
求\(\mu_{k}\)解
\[\mu_{k} = \frac{f_{k}}{N} = \frac{f_{k}}{w \cos 25^{o}} = \frac{f_{k}}{mg \cos 25^{o}} \ldotp\]
用方程右侧的已知值代替,
\[\mu_{k} = \frac{45.0\; N}{(62\; kg)(9.80\; m/s^{2})(0.906)} = 0.082 \ldotp\]
意义
该结果略小于表 6.1 中列出的雪地上打蜡木材的系数,但仍然合理,因为摩擦系数的值可能会有很大差异。 在这种情况下,质量为 m 的物体沿着\(\theta\)与水平方向成一定角度的斜率滑动,摩擦力由 f k =\(\mu_{k}\) mg cos 给出\(\theta\)。 在这种情况下,所有物体都会以恒定的加速度向下滑动。
我们已经讨论过,当物体停留在水平表面上时,支撑它的法向力在幅度上等于其重量。 此外,简单的摩擦力始终与法向力成正比。 当物体不在水平表面上时,就像倾斜的平面一样,我们必须找到作用在物体上的垂直于表面的力;它是重量的一个组成部分。
现在,我们推导出了一个有用的关系来计算倾斜平面上的摩擦系数。 请注意,结果仅适用于物体以恒定速度向下滑动的情况。
如果物体上的净力为零,则物体以恒定速度向下滑动。 我们可以利用这个事实来测量两个物体之间的动摩擦系数。 如示例所示\(\PageIndex{1}\),斜坡上的动摩擦力为 f k =\(\mu_{k}\) mg cos\(\theta\)。 斜率下方的重量分量等于 mg sin\(\theta\)(参见图中的自由体图\(\PageIndex{1}\))。 这些力在相反的方向上起作用,因此,当它们的幅度相等时,加速度为零。 把这些写出来,
\[\mu_{k} mg \cos \theta = mg \sin \theta \ldotp\]
求解\(\mu_{k}\),我们发现了
\[\mu_{k} = \frac{mg \sin \theta}{mg \cos \theta} = \tan \theta \ldotp\]
将硬币放在书上,然后将其倾斜,直到硬币以恒定的速度向下滑动。 你可能需要轻点这本书才能让硬币移动。 测量相对于水平的倾斜角度,然后找到\(\mu_{k}\)。 请注意,由于静摩擦系数大\(\theta\)于动摩擦系数,硬币直到达到大于角度的角度才会开始滑动。 想想这会如何影响价值\(\mu_{k}\)及其不确定性。
摩擦的原子尺度解释
到目前为止,处理的摩擦力更简单的方面是其宏观(大规模)特征。 在过去的几十年中,在原子尺度解释摩擦方面取得了长足的进步。 研究人员发现,摩擦的原子性质似乎有几个基本特征。 这些特性不仅解释了摩擦的一些更简单的方面,而且还有可能发展出几乎无摩擦的环境,从而节省数千亿美元的能量,而这些能量目前正在(不必要地)转化为热能。
该图\(\PageIndex{2}\)说明了微观(小规模)研究解释的摩擦的一个宏观特征。 我们已经注意到,摩擦力与法向力成正比,但与接触面积成正比,这是一个有点违反直觉的概念。 当两个粗糙表面接触时,实际接触面积只占总面积的一小部分,因为只有高点会接触。 当施加更大的法向力时,实际接触面积就会增加,我们发现摩擦力与该面积成正比。
但是,原子尺度视图有望解释的远不止是摩擦的简单特征。 目前正在确定如何产生热量的机制。 换句话说,为什么摩擦表面会变热? 本质上,原子相互连接形成晶格。 当表面摩擦时,表面原子会粘附并导致原子晶格振动,本质上是产生穿透材料的声波。 声波随着距离而减弱,它们的能量被转化为热量。 与摩擦磨损有关的化学反应也可能发生在表面上的原子和分子之间。 该图\(\PageIndex{3}\)显示了在另一种材料上绘制的探针尖端是如何因原子尺度摩擦而变形的。 拖动尖端所需的力是可以测量的,发现它与剪切应力有关,静态平衡和弹性中对此进行了讨论。 剪应力的变化非常显著(超过1012倍),理论上难以预测,但是剪应力使人们对自古以来已知的大规模现象——摩擦有了基本的了解。
描述分子层面的摩擦模型。 用分子运动描述物质。 描述应包括支持描述的图表;温度如何影响图像;固体、液体和气体颗粒运动之间有什么区别和相似之处;以及气体分子的大小和速度与日常物体有何关系。
Figur\(\PageIndex{4}\) e 的两个方块由一根无质量的绳子相互连接,该绳子缠绕在无摩擦滑轮上。 当底部的 4.00 千克方块被恒定力拉向左时\(\vec{P}\),顶部 2.00 千克的方块会向右滑过。 找出以恒定速度移动方块所需的力的大小。 假设所有表面之间的动摩擦系数为 0.400。
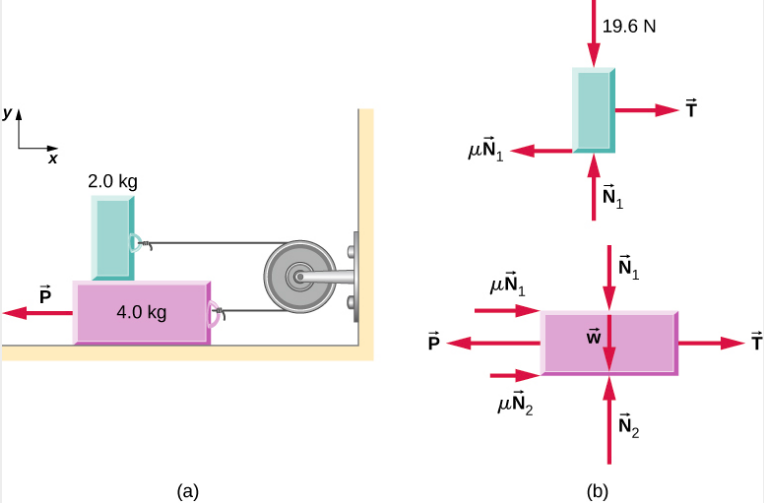
策略
我们分别分析两个方块的运动。 顶部块受到底部块施加的接触力。 该力的组成部分是法向力 N 1 和摩擦力 −0.400 N 1。 顶部方块上的其他力是绳子中的张力 T 和顶部方块本身的重量 19.6 N。底部方块由于顶部方块和地板而受到接触力。 第一个接触力的分量为 −N 1 和 0.400 N 1,它们只是对底部方块施加在顶部方块上的接触力的反作用力。 地板接触力的分量为 N 2 和 0.400 N 2。 该方块上的其他力是 −P、张力 T 和权重 —39.2 N。解决方案由于顶部方块以恒定速度水平向右移动,因此其在水平和垂直方向上的加速度均为零。 根据牛顿第二定律,
|
\[\sum F_{x} = m_{2} a_{x}\] \[T - 0.400\; N_{1} = 0\] |
\[\sum F_{y} = m_{1} a_{y}\] \[N_{1} - 19.6\; N = 0 \ldotp\] |
求解两个未知数,我们得到 N 1 = 19.6 N 和 T = 0.40 N 1 = 7.84 N 底部方块也没有加速,因此将牛顿第二定律应用于这个方块可以得出
|
\[\sum F_{x} = m_{2} a_{x}\] \[T - P + 0.400\; N_{1} + 0.400\; N_{2} = 0\] |
\[\sum F_{y} = m_{1} a_{y}\] \[N_{2} - 39.2\; N - N_{1} = 0 \ldotp\] |
N 1 和 T 的值是用第一组方程找到的。 当这些值被替换成第二组方程时,我们可以确定 N 2 和 P。它们是
\[N_{2} = 58.8\; N\; and\; P = 39.2\; N \ldotp\]
意义
要了解向哪个方向施加摩擦力通常很麻烦。 请注意,图中标记的每种摩擦力的\(\PageIndex{4}\)作用方向与其对应方块的运动方向相反。
一个 50.0 千克的箱子放在卡车的底座上,如图所示\(\PageIndex{5}\)。 表面之间的摩擦系数为\(\mu_{k}\) = 0.300 和\(\mu_{s}\) = 0.400。 找出卡车以 (a) 2.00 m/s 2 和 (b) 5.00 m/s 2 的速度相对于地面向前加速时箱子上的摩擦力。
策略
箱子上的力是其重量以及由于与卡车底盘接触而产生的法向力和摩擦力。 我们首先假设箱子没有滑落。 在这种情况下,静态摩擦力 fs 作用于箱子。 此外,箱子和卡车的加速度是相等的。
解决方案
- 使用附着在地面的参考系将牛顿第二定律应用于箱子,会产生
\[\begin{split} \sum F_{x} & = ma_{x} \\ f_{s} & = (50.0\; kg)(2.00\; m/s^{2}) \\ & = 1.00 \times 10^{2}\; N \end{split}\]
\[\begin{split} \sum F_{y} & = ma_{y} \\ N - 4.90 \times 10^{2}\; N & = (50.0\; kg)(0) \\ N & = 4.90 \times 10^{2}\; N \ldotp \end{split}\]
我们现在可以检查我们的 “不滑落” 假设的有效性。 静摩擦力的最大值为 $$\ mu_ {s} N = (0.400) (4.90\ times 10^ {2}\; N) = 196\; N, $$而卡车以 2.00 m/s 2 向前加速时起作用的实际静摩擦力仅为 1.00 x 10 2 N。因此,假设没有滑动是有效的。
- 如果箱子在 5.0 m/s 2 加速时随卡车移动,则静摩擦力必须为 $$f_ {s} = ma_ {x} = (50.0\; kg) (5.00\; m/s^ {2}) = 250\; N\ ldotp$由于超过最大值 196 N,因此箱子必须滑动。 因此,摩擦力是动力学的,为 $$f_ {k} =\ mu_ {k} N = (0.300) (4.90\ times 10^ {2}\; N) = 147\; N\ ldotp$现在可以从 $$\ begin {split}\ sum F_ {x} & = ma_ {x}\\ 147; N & = (50.0\; kg) a_ {x},\\ so\; a_ {x} & = 2.94\; m/s^ {2}\ ldotp\ end {split}\]
意义
相对于地面,卡车以 5.0 m/s 2 的速度向前加速,板条箱以 2.94 m/s 2 的速度向前加速。 因此,箱子相对于卡车底座向后滑动,加速度为 2.94 m/s 2 − 5.00 m/s 2 = −2.06 m/s 2。
早些时候,我们分析了速降滑雪运动员以恒定速度移动的情况,以确定动摩擦系数。 现在让我们做一个类似的分析来确定加速度。 Figure 的\(\PageIndex{6}\)滑雪板运动员沿着向水平倾斜度为\(\theta\) = 13° 的斜坡滑行。 板和雪之间的动摩擦系数为\(\mu_{k}\) = 0.20。 滑雪板运动员的加速度是多少?
策略
作用于滑雪板运动员的力是她的体重和斜坡的接触力,斜坡有一个垂直于斜坡的分量和一个沿斜坡的分量(动摩擦力)。 因为她沿着斜坡移动,所以分析她运动的最方便的参考系是 x 轴沿着斜坡移动,y 轴垂直于斜坡的参考系。 在此帧中,法向力和摩擦力均位于坐标轴\(\theta\)上,权重的分量是沿斜率的 mg sin β 和与斜率成直角的 mg cos,唯一的加速度是沿 x 轴(a y = 0)。
解决方案
现在,我们可以将牛顿第二定律应用到滑雪板运动员身上:
|
\[\begin{split} \sum F_{x} & = ma_{x} \\ mg \sin \theta - \mu_{k} N & = ma_{x} \end{split}\] |
\[\begin{split} \sum F_{y} & = ma_{y} \\ N - mg \cos \theta &= m(0) \ldotp \end{split}\] |
根据第二个方程,N = mg cos\(\theta\)。 用这个代入第一个方程后,我们发现
\[\begin{split} a_{x} & = g(\sin \theta - \mu_{k} \cos \theta) \\ & = g(\sin 13^{o} - 0.520 \cos 13^{o}) = 0.29\; m/s^{2} \ldotp \end{split}\]
意义
从这个方程中可以看出,如果\(\theta\)足够小或\(\mu_{k}\)足够大,x 是负数,也就是说,滑雪板运动员会减速。
滑雪板运动员现在正沿着斜度为 10.0° 的山坡移动。 滑雪者的加速度是多少?


