4.6: 一维和二维的相对运动

Last updated
Save as PDF

Page ID: 204907

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

学习目标

解释参考框架的概念。
写出相对运动的位置和速度矢量方程。
绘制相对运动的位置和速度向量。
使用位置和速度矢量方程分析一维和二维相对运动问题。

运动不是孤立发生的。如果您乘坐的是以10 m/s的速度向东行驶的火车，则该速度是相对于您行驶的地面进行测量的。但是，如果另一列火车以东 15 m/s 的速度通过您，则您相对于另一列火车的速度与您相对于地面的速度不同。您相对于另一列火车的速度为向西 5 m/s。为了进一步探索这个想法，我们首先需要建立一些术语。

参考框架

为了讨论一个或多个维度的相对运动，我们首先介绍参考系的概念。当我们说一个物体具有一定的速度时，我们必须声明它具有相对于给定参考系的速度。在我们到目前为止研究的大多数例子中，这个参考框架都是地球。如果你说一个人坐在火车上以10 m/s的速度向东移动，那么你就意味着火车上的人正在以这个速度相对于地球表面移动，而地球是参考框架。我们可以扩大对火车上人运动的视野，说地球在绕太阳的轨道上旋转，在这种情况下，运动变得更加复杂。在这种情况下，太阳系是参考框架。总而言之，所有关于相对运动的讨论都必须定义所涉及的参考框架。我们现在开发了一种在相对运动中引用参考帧的方法。

一维相对运动

我们首先引入一维的相对运动，因为速度向量简化为只有两个可能的方向。以坐在火车上向东行驶的人为例。如果我们选择东方作为正方向，选择地球作为参考坐标，那么我们可以将列车相对于地球的速度写成$\vec{v}_{TE}$ = 10 m/s 向$\hat{i}$东，下标 TE 表示火车和地球。现在假设这个人从她的座位上站起来，以 2 m/s 的速度向火车后部行走。这告诉我们她的速度相对于列车的参考坐标系而言是相对于列车的参考坐标系的。由于该人正朝负方向向西行走，因此我们将她相对于火车的速度写成$\vec{v}_{PT}$ = −2 m/s$\hat{i}$。我们可以将两个速度向量相加以求出人相对于地球的速度。这个相对速度写成

\[\vec{v}_{PE} = \vec{v}_{PT} + \vec{v}_{TE} \ldotp \label{4.33}\]

注意方程\ ref {4.33} 中各种参考系的下标顺序。耦合参考系（即列车）的下标连续出现在方程的右侧。该图$\PageIndex{1}$显示了形成矢量方程时下标的正确顺序。

alt — 图$\PageIndex{1}$：构造矢量方程时，耦合参考系的下标连续出现在内部。方程左侧的下标与方程右侧的两个外部下标相同。

将向量相加，我们发现$\vec{v}_{PE}$ = 8 m/s$\hat{i}$，因此该人相对于地球向东移动 8 m/s。图形上，如图所示$\PageIndex{2}$。

列车相对于地球的速度向量、人相对于列车的速度矢量以及人相对于地球的速度向量。 V sub T E 是列车相对于地球的速度矢量。它的值为每秒 10 米，表示为指向右侧的绿色长箭头。 V sub P T 是人相对于列车的速度矢量。它的值为 -2 米/秒，表示为指向左侧的绿色短箭头。 V sub P E 是人相对于地球的速度矢量。它的值为每秒 8 米，表示为指向右侧的中等长度的绿色箭头。 — 图$\PageIndex{2}$：列车相对于地球的速度向量、人相对于列车的速度矢量以及人相对于地球的速度向量。

二维相对速度

现在，我们可以应用这些概念来描述二维运动。假设一个粒子 P 和参考帧 S 和 S′，如图所示$\PageIndex{3}$。在 S 中测量的 S′ 原点的位置为$\vec{r}_{S'S}$，以 S′ 测量的 P 的位置为$\vec{r}_{PS'}$，在 S 中测量的 P 的位置为$\vec{r}_{PS}$。

x y z 坐标系显示并标记为系统 S。第二个坐标系，即轴为 x 素数、y 素数、z 素数的 S prime 相对于 S 移动。向量 r sub S prime S（显示为紫色箭头）从 S 的原点延伸到 S 素数的原点。向量 r sub P S 是从 S 原点到点 P 的向量。向量 r sub P S prime 是从 S 素数原点到同一点 P 的向量。向量 r s 素数 s、r P S 素数和 r P S 构成三角形，r P S 是 r S 素数 S 和 r P S 素数的向量和。 — 图$\PageIndex{3}$：粒子 P 相对于帧 S 和 S′ 的位置分别为和。$\vec{r}_{PS}$$\vec{r}_{PS'}$

从图中$\PageIndex{3}$我们可以看出

\[\vec{r}_{PS} = \vec{r}_{PS} + \vec{r}_{S'S} \ldotp \label{4.34}\]

相对速度是位置向量的时间导数。因此，

\[\vec{v}_{PS} = \vec{v}_{PS'} + \vec{v}_{S'S} \ldotp \label{4.35}\]

粒子相对于 S 的速度等于其相对于 S′ 的速度加上 S′ 相对于 S 的速度

我们可以将方程\ ref {4.35} 扩展到任意数量的参考系。对于速度为、的粒子 P$\vec{v}_{PA}$$\vec{v}_{PB}$，$\vec{v}_{PC}$在 A、B 和 C 帧中，

\[\vec{v}_{PC} = \vec{v}_{PA} + \vec{v}_{AB} + \vec{v}_{BC} \ldotp \label{4.36}\]

我们还可以通过微分方程\ ref {4.35} 来查看在两个参考系中观察到的加速度之间的关系：

\[\vec{a}_{PS} = \vec{a}_{PS'} + \vec{a}_{S'S} \ldotp \label{4.37}\]

我们可以看到，如果 S′ 相对于 S 的速度是一个常数，那么$\vec{a}_{S'S}$ = 0 和

\[\vec{a}_{PS} = \vec{a}_{PS'} \ldotp \label{4.38}\]

也就是说，粒子的加速度与两个观察者相对于彼此以恒定速度移动所测得的加速度相同。

示例 4.13：汽车相对于卡车的运动

一辆卡车以 70 km/h 的速度向南驶向十字路口。一辆汽车以 80 km/h 的速度向东驶向十字路口（图$\PageIndex{4}$）。汽车相对于卡车的速度是多少？

显示一辆卡车以 70 km/h 的速度 V sub T E 向南行驶，驶向十字路口。一辆汽车以 80 km/h 的速度 V sub C E 向东驶向十字路口 — 图$\PageIndex{4}$：一辆汽车向东驶向十字路口，而一辆卡车向南驶向同一个十字路口。

策略

首先，我们必须建立两种飞行器共同的参考框架，即地球。然后，我们写出每种速度相对于地球参考系的速度，这使我们能够形成一个将汽车、卡车和地球联系起来的矢量方程，以求解汽车相对于卡车的速度。

解决方案

汽车相对于地球的速度$\vec{v}_{CE}$为 80 km/h$\hat{i}$。卡车相对于地球的速度$\vec{v}_{TE}$为 −70 km/h$\hat{j}$。使用速度加法规则，我们正在寻找的相对运动方程是

\[\vec{v}_{CT} = \vec{v}_{CE} + \vec{v}_{ET} \ldotp \label{ex2}\]

这里$\vec{v}_{CT}$是汽车相对于卡车的速度，地球是连接的参考框架。由于我们有卡车相对于地球的速度，因此该向量的负值是地球相对于卡车的速度：$\vec{v}_{ET} = − \vec{v}_{TE}$。该方程的矢量图如图所示$\PageIndex{5}$。

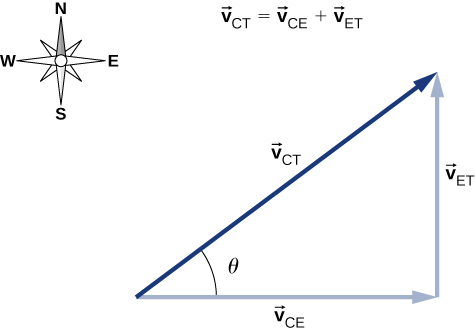
由右边的向量 V sub C E、向下 V sub E T 和 V sub C T 向上和向右形成的直角三角形显示为 V sub C T 是斜边，与 V sub C E 成了 theta 的角度。显示的指南针表示北向上，东向右，南向下，西向左。 — 图$\PageIndex{5}$：矢量方程\ ref {ex2} 的矢量图。

我们现在可以求解汽车相对于卡车的速度：

\[\big| \vec{v}_{CT} \big| = \sqrt{(80.0\; km/h)^{2} + (70.0\; km/h)^{2}} = 106.\; km/h \nonumber\]

和

\[\theta = \tan^{-1} \left(\dfrac{70.0}{80.0}\right) = 41.2^{o}\; north\; of\; east \ldotp \nonumber\]

意义

绘制显示速度向量的矢量图可以帮助理解两个物体的相对速度。

练习 4.6

一艘船在静水中以 4.5 m/s 的速度向北行驶，直接穿过一条以 3.0 m/s 的速度向东延伸的河流。船相对于地球的速度是多少？

示例 4.14：在风中驾驶飞机

飞行员必须向北驾驶飞机才能到达目的地。飞机可以在静止空气中以 300 km/h 的速度飞行。风以 90 km/h 的速度从东北吹出。(a) 飞机相对于地面的速度是多少？ (b) 飞行员必须朝哪个方向开飞机才能向北飞行？

策略

飞行员必须将飞机指向北偏东，以补偿风速。我们需要构造一个矢量方程，其中包含飞机相对于地面的速度、飞机相对于空气的速度以及空气相对于地面的速度。由于最后两个量是已知的，我们可以求解飞机相对于地面的速度。我们可以绘制向量图，然后使用此图来评估飞机相对于地面的速度的大小。该图还将告诉我们飞机的速度与北方相对于空气的角度，这是飞行员必须驾驶飞机的方向。

解决方案

向量方程为$\vec{v}_{PG} = \vec{v}_{PA} + \vec{v}_{AG}$，其中 P = 平面，A = 空气，G = 地面。从图中的几何图形来看$\PageIndex{6}$，我们可以很容易地求解飞机相对于地面的速度的大小和飞机的航向角度$\theta$。

指南针显示北向上，东向右，南向下，西向左。向量 V sub P G、V sub A G 和 V sub P A 形成三角形。飞机显示在向量 V sub P G 上，它指向上方。 V sub P A 向上和向右指向，以 theta 与向量 V sub P G 的角度向上和向右指向 V sub P G 向下和向左指向，角度低于水平线 45 度。 V sub P G 是 v sub P A 和 V sub A G 的矢量和 — 图$\PageIndex{6}$：显示向量$\vec{v}_{PA}$、$\vec{v}_{AG}$和的方程\ ref {4.34} 的矢量图$\vec{v}_{PG}$。

已知数量：$$\ big|\ vec {v} _ {PA}\ big| = 300\; km/h$$ $$\ big|\ vec {v} _ {AG}\ big| = 90\; km/H$$代入运动方程后，我们得到$\big| \vec{v}_{PG} \big|$ = 230 km/h。
角度$\theta$ = tan ⁻¹$\left(\dfrac{63.64}{300}\right)$ = 北向东 12°。