4.5: 均匀的圆周运动
- Page ID
- 204911
- 求解在圆形路径上移动的物体的向心加速度。
- 使用圆周运动方程来计算执行圆周运动的粒子的位置、速度和加速度。
- 解释不均匀的圆周运动导致的向心加速度和切向加速度之间的差异。
- 评估非均匀圆周运动中的向心和切向加速度,并找到总加速度向量。
均匀的圆周运动是一种特定类型的运动,在这种运动中,物体以恒定的速度绕圈移动。 例如,螺旋桨上以恒定速度旋转的任何点都在执行均匀的圆周运动。 其他示例包括手表的秒针、分针和时针。 值得注意的是,尽管旋转速度是恒定的,但这些旋转物体上的点实际上正在加速。 要看到这一点,我们必须用向量来分析运动。
向心加速
在一维运动学中,恒定速度的物体的加速度为零。 但是,在二维和三维运动学中,即使速度是恒定的,如果粒子沿着曲线轨迹(例如圆)移动,它也可以加速。 在这种情况下,速度矢量正在变化,或\(\frac{d\vec{v}}{dt}\) ≤ 0。 如图所示\(\PageIndex{1}\)。 当粒子在圆形路径上的时间\(\Delta\) t 中逆时针移动时,其位置向量从移动\(\vec{r}(t)\)到\(\vec{r}(t + \Delta t)\)。 速度向量具有恒定大小,并且在路径从\(\vec{v}\) (t) 变为 (t) 时与路径相切\(\vec{v}\left(t + \Delta t\right)\),仅改变其方向。 由于速度向量\(\vec{v}(t)\)垂直于位置向量\(\vec{r}\) (t),因此由位置向量和、以及速度向量和\(\Delta \vec{r}\)形成的三角形\(\Delta \vec{v}\)是相似的。 此外,由于
\[|\vec{r}(t) | = | \vec{r} (t + \Delta t)| \nonumber\]
和
\[| \vec{v} (t)| = | \vec{v} (t + \Delta t)|, \nonumber \]
这两个三角形是等腰线。 根据这些事实,我们可以做出断言
\[\dfrac{\Delta v}{v} = \dfrac{\Delta r}{r}\]
要么
\[\Delta v = \dfrac{v}{r} \Delta r.\]
我们可以从中找到加速度的大小
\[a = \lim_{\Delta t \rightarrow 0} \left(\dfrac{\Delta v}{\Delta t}\right) = \frac{v}{r} \left(\lim_{\Delta t \rightarrow 0} \dfrac{\Delta r}{\Delta t}\right) = \frac{v^{2}}{r} \ldotp\]
也可以通过以下方式找到加速度的方向:当\(\Delta\) t 因此\(\Delta \theta\)接近零时,矢量\(\Delta \vec{v}\)接近垂直于的方向\(\vec{v}\)。 在极\(\Delta t → 0,\)\(\Delta \vec{v}\)限中垂直于\(\vec{v}\)。 \(\vec{v}\)由于与圆相切,因此加速度\(\frac{d \vec{v}}{dt}\)指向圆的中心。 总而言之,以恒定速度在圆圈中移动的粒子的加速度为幅度
\[a_{c} = \frac{v^{2}}{r} \ldotp \label{4.27}\]
加速度向量的方向朝向圆的中心(图\(\PageIndex{2}\))。 这是一种径向加速度,被称为向心加速度,这就是我们给它下标的原因\(c\)。 向心这个词来自拉丁语 cent rum(意思是 “中心”)和 p etere(意思是 “寻找”),因此其含义是 “中心寻找”。
让我们研究一些例子,说明速度、半径和向心加速度的相对幅度。
喷气式飞机以134.1 m/s的速度沿直线飞行,并沿着与地面的圆形路径水平转弯。 要使飞行员和喷气机朝向圆形轨迹中心产生 1 g 的向心加速度,圆的半径必须是多少?
策略
给定喷气的速度,我们可以在向心加速度表达式中求解圆的半径。
解决方案
将向心加速度设置为等于重力加速度:9.8 m/s 2 =\(\frac{v^{2}}{r}\)。
求解半径,我们发现
\[r = \frac{(134.1\; m/s)^{2}}{9.8\; m/s^{2}} = 1835\; m = 1.835\; km \ldotp\]
意义
要在飞行员身上产生大于 g 的加速度,喷气式飞机要么必须减小其圆形轨迹的半径,要么提高其现有轨迹的速度,要么两者兼而有之。
飞轮的半径为 20.0 厘米。 如果飞轮边缘某个点的向心加速度为 900.0 cm/s 2,它的速度是多少?
向心加速度的值范围很广,具体取决于圆形路径的速度和曲率半径。 表中给出了典型的向心加速度\(\PageIndex{1}\)。
| 物体 | 向心加速度(m/s 2 或 g 系数) |
|---|---|
| 环绕太阳的地球 | 5.93 x 10 -3 |
| 环绕地球的月亮 | 2.73 x 10 -3 |
| 地球同步轨道上的卫星 | 0.233 |
| 播放时 CD 的外缘 | 5.75 |
| 在桶里喷射飞机 | (2-3 g) |
| 过山车 | (5 g) |
| 在简单的玻尔原子模型中,电子绕质子运行 | 9.0 x 10 22 |
均匀圆周运动的运动方程
执行圆周运动的粒子可以用其位置向量来描述\(\vec{r}(t)\)。 图中\(\PageIndex{3}\)显示了粒子沿逆时针方向执行圆周运动。 当粒子在圆上移动时,其位置向量会扫除\(\theta\)与 x 轴的角度。 显示\(\theta\)与 x 轴成角度的矢量\(\vec{r}(t)\)及其沿 x 轴和 y 轴的分量。 位置向量的大小是\(A = |\vec{r}(t)|\)而且也是圆的半径,因此就其分量而言,
\[\vec{r} (t) = A \cos \omega \hat{i} + A \sin \omega t \hat{j} \ldotp \label{4.28}\]
这里\(\omega\)是一个常数,称为粒子的角频率。 角频率以每秒弧度 (rad) 为单位,只是粒子每秒通过的角度测量的弧度数。 位置向量在任何特定时间的角度\(θ\)为\(\omega\) t。
如果\(T\)是运动周期,或者是完成一圈的时间 (\(2 \pi\, rad\)),那么
速度和加速度可以通过微分从位置函数中获得:
\[\vec{v} (t) = \frac{d \vec{r} (t)}{dt} = -A \omega \sin \omega t \hat{i} + A \omega \cos \omega t \hat{j} \ldotp \label{4.29}\]
从图中可以看出\(\PageIndex{3}\),速度矢量与粒子所在位置的圆相切,幅度为 A\(\omega\)。 同样,加速度矢量是通过微分速度来找到的:
\[\vec{a} (t) = \frac{d \vec{v} (t)}{dt} = -A \omega^{2} \cos \omega t \hat{i} - A \omega^{2} \sin \omega t \hat{j} \ldotp \label{4.30}\]
从这个方程中我们可以看出,加速度向量的幅度为 A,\(\omega^{2}\)并且与位置向量相反,朝向原点,因为\(\vec{a}\) (t) = −\(\omega^{2} \vec{r}\) (t)。
质子的速度为 5 x 10 6 m/s,在半径为 r = 0.175 m 的 xy 平面上围成一个圆移动。当时间 t = 2.0 x 10 −7 s = 200 ns 时,它在 xy 平面中的位置是什么? t = 0 时,质子的位置为 0.175 m\(\hat{i}\),它逆时针旋转。 草绘轨迹。
解决方案
根据给定的数据,质子具有周期和角频率:
\[T = \frac{2 \pi r}{v} = \frac{2 \pi (0.175\; m)}{5.0 \times 10^{6}\; m/s} = 2.20 \times 10^{-7}\; s \nonumber \]
\[\omega = \frac{2 \pi}{T} = \frac{2 \pi}{2.20 \times 10^{-7}\; s} = 2.856 \times 10^{7}\; rad/s \ldotp \nonumber \]
粒子在 t = 2.0 x 10 −7 s 和 A = 0.175 m 处的位置为
\[\begin{align*} \vec{r} (2.0 \times 10^{-7}\; s) & = A \cos \omega (2.0 \times 10^{-7}\; s) \hat{i} + A \sin \omega (2.0 \times 10^{-7}\; s) \hat{j}\; m \\[4pt] & = 0.175 \cos (2.856 \times 10^{7}\; rad/s) (2.0 \times 10^{-7}\; s) \hat{i} + 0.175 \sin (2.856 \times 10^{7}\; rad/s) (2.0 \times 10^{-7}\; s) \hat{j}\; m \\[4pt] & = 0.175 \cos (5.712\; rad) \hat{i} + 0.175 \sin (5.172\; rad) \hat{j}\; m \\ & = 0.147 \hat{i} - 0.095 \hat{j}\; m \ldotp \end{align*}\]
从这个结果中我们可以看出,质子位于 x 轴略低于 x 轴。 如图所示\(\PageIndex{4}\)。
意义
我们选择了粒子的初始位置在 x 轴上。 这完全是武断的。 如果给出不同的起始位置,则在 t = 200 ns 时我们将得到不同的最终位置。
非均匀的圆周运动
圆周运动不必保持恒定速度。 粒子可以围成一圈移动并加速或减速,显示运动方向上的加速度。
在均匀的圆周运动中,执行圆周运动的粒子具有恒定的速度,圆的半径是固定的。 如果粒子的速度也在变化,那么我们在与圆的切线方向上引入额外的加速度。 这种加速度发生在顶部改变其自旋速率的某个点或任何加速转子。 在位移和速度向量中,我们展示了向心加速度是速度向量方向的时间变化率。 如果粒子的速度发生变化,则它具有切向加速度,即速度大小的时间变化率:
\[a_{T} = \frac{d |\vec{v}|}{dt} \ldotp \label{4.31}\]
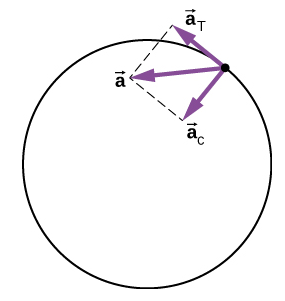
切向加速度的方向与圆相切,而向心加速度的方向是朝向圆心的径向内向。 因此,圆周运动中具有切向加速度的粒子的总加速度是向心加速度和切向加速度的矢量和:
\[\vec{a} = \vec{a}_{c} + \vec{a}_{T} \ldotp \label{4.32}\]
加速度向量如图所示\(\PageIndex{5}\)。 请注意,两个加速度向\(\vec{a}_{T}\)量\(\vec{a}_{c}\)和彼此垂直,\(\vec{a}_{c}\)在径向方向和\(\vec{a}_{T}\)切向方向上。 总加速度\(\vec{a}\)指向介于\(\vec{a}_{c}\)和之间的某个角度\(\vec{a}_{T}\)。
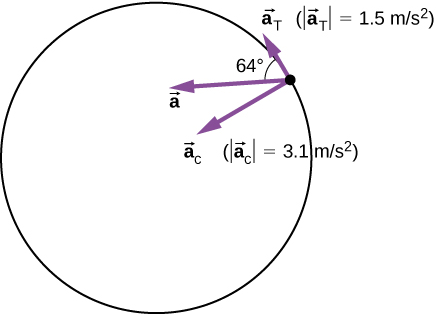
粒子在半径为 r = 2.0 m 的圆中移动。在从 t = 1.5 秒到 t = 4.0 秒的时间间隔内,其速度随时间而变化
\[v(t) = c_{1} - \frac{c_{2}}{t^{2}}, c_{1} = 4.0\; m/s, c_{2} = 6.0\; m \cdotp s \ldotp\]
t = 2.0 秒时粒子的总加速度是多少?
策略
我们被赋予了粒子的速度和圆的半径,因此我们可以轻松计算向心加速度。 向心加速度的方向是朝向圆的中心。 我们通过使用方程\ ref {4.31} 取相对于时间 |v (t) | 的导数并在 t = 2.0 秒时对其进行计算,得出切向加速度的大小。我们使用该值和向心加速度的大小来求出总加速度。
解决方案
向心加速度为
\[v(2.0\; s) = \left(4.0 - \dfrac{6.0}{(2.0)^{2}}\right) m/s = 2.5\; m/s \nonumber \]
\[a_{c} = \frac{v^{2}}{r} = \frac{(2.5\; m/s)^{2}}{2.0\; m} = 3.1\; m/s^{2} \nonumber \]
指向圆的中心。 切向加速度为
\[a_{T} = \Big| \frac{d \vec{v}}{dt} \Big| = \frac{2 c_{2}}{t^{3}} = \frac{12.0}{(2.0)^{3}} m/s^{2} = 1.5\; m/s^{2} \ldotp \nonumber \]
总加速度为
\[|\vec{a}| = \sqrt{3.1^{2} + 1.5^{2}} m/s^{2} = 3.44\; m/s^{2}\]
并\(\theta\)且 = tan −1\(\left(\dfrac{3.1}{1.5}\right)\) = 距离圆的切线的 64°。 参见图\(\PageIndex{6}\)。
意义
可以用极坐标系更方便地描述向心和切向加速度的方向,单位向量位于径向和切向方向。 该坐标系用于沿曲线路径运动,本书后面将详细讨论该坐标系。


