4.4: 射弹运动

Last updated
Save as PDF

Page ID: 204895

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

学习目标

使用垂直方向上的一维运动来分析弹丸的运动。
计算发射并撞击平坦的水平表面的弹丸的射程、飞行时间和最大高度。
找出着陆高度与发射高度不同的弹丸的飞行时间和冲击速度。
计算弹丸的轨迹。

弹丸运动是物体向空中投掷或投射的运动，仅受重力加速。射弹运动在物理和工程中的应用很多。一些例子包括流星进入地球大气层时、烟花以及体育运动中任何球的运动。这样的物体被称为射弹，它们的路径被称为轨迹。在 “沿直线运动” 中讨论的坠落物体的运动是一种简单的一维弹丸运动，其中没有水平移动。在本节中，我们将考虑二维弹丸运动，而我们的处理方法忽略了空气阻力的影响。

这里要记住的最重要的事实是，沿垂直轴的运动是独立的，因此可以单独分析。我们在位移和速度向量中讨论了这个事实，我们看到垂直运动和水平运动是独立的。分析二维弹丸运动的关键是将其分为两个运动：一个沿水平轴运动，另一个沿垂直运动。（这种轴的选择是最明智的，因为重力产生的加速度是垂直的；因此，当空气阻力可以忽略不计时，不会沿水平轴加速。）按照惯例，我们将水平轴称为 x 轴，将垂直轴称为 y 轴。我们不必使用这种轴的选择；在引力加速度的情况下，这很方便。在其他情况下，我们可以选择一组不同的轴。该图$\PageIndex{1}$说明了位移的表示法，其中我们定义$\vec{s}$为总位移，$\vec{x}$和分别$\vec{y}$是其沿水平轴和垂直轴的分量向量。这些向量的大小为 s、x 和 y。

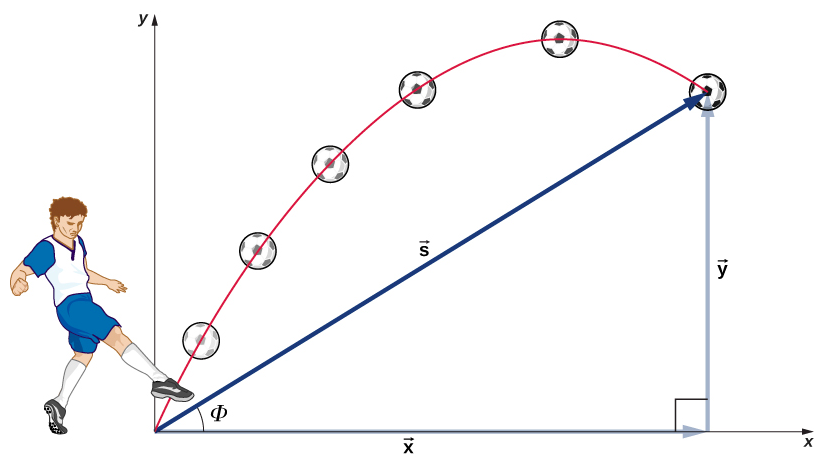
足球运动员踢球的插图。足球运动员的脚位于 x y 坐标系的原点。显示了足球的轨迹及其在 6 个瞬间的位置。轨迹是抛物线。向量 s 是足球从原点到最终位置的位移。向量 s 及其 x 和 y 分量形成一个直角三角形，其中 s 作为斜边，x 轴和 s 之间的角度 phi。 — 图$\PageIndex{1}$：足球在其路径上某一点的总位移量。向量$\vec{s}$具有分量$\vec{x}$，$\vec{y}$沿水平轴和垂直轴行驶。它的大小为 s，它$\phi$与水平方向成一个角度。

为了完整地描述弹丸的运动，我们必须包括速度和加速度以及位移。我们必须沿着x轴和y轴找到它们的分量。假设除重力（例如空气阻力和摩擦力）之外的所有力都可以忽略不计。将正方向定义为向上，那么加速度的分量就非常简单了：

\[a_{y} = −g = −9.8\; m/s^{2} (− 32\; ft/s^{2}) \ldotp\]

因为重力是垂直的，所以 a _x = 0。如果 a _x = 0，则表示 x 方向上的初始速度等于 x 方向上的最终速度，或 v _x = v _0x。有了这些关于加速度和速度的条件，我们可以编写运动学方程 4.11 至方程 4.18，用于均匀引力场中的运动，包括其余运动方程以恒定加速度从运动中获得恒定加速度。均匀引力场中运动的运动学方程变成 a = −g，a _{_x} = 0 的运动学方程：

水平运动

\[v_{0x} = v_{x}, \quad x = x_{0} + v_{x} t \label{4.19}\]

垂直运动

\[y = y_{0} + \frac{1}{2} (v_{0y} + v_{y})t \label{4.20}\]

\[v_{y} = v_{0y} - gt \label{4.21}\]

\[y = y_{0} + v_{0y} t - \frac{1}{2} g t^{2} \label{4.22}\]

\[v_{y}^{2}= v_{0y}^{2} + 2g(y − y_{0}) \label{4.23}\]

使用这组方程，我们可以分析弹丸的运动，同时牢记一些要点。

问题解决策略：射弹运动

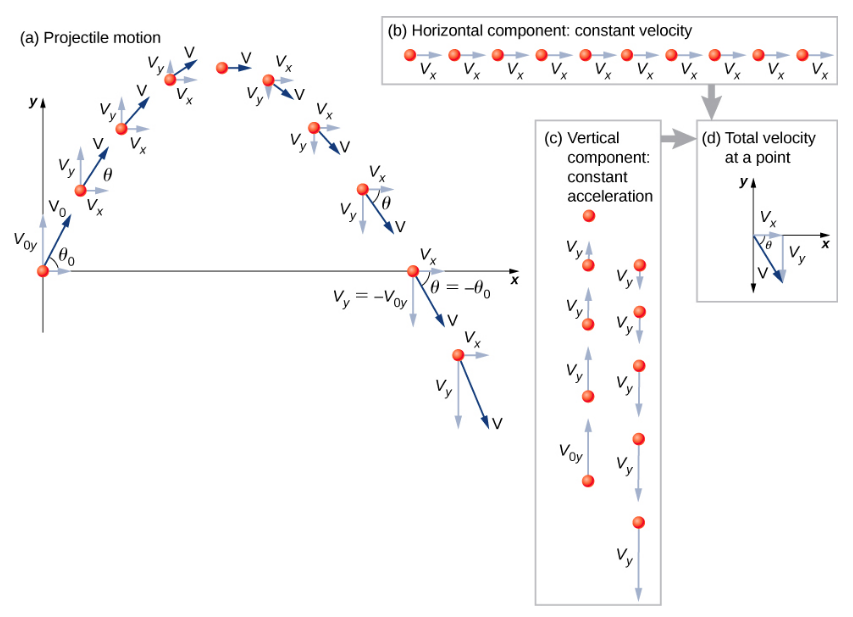
将运动解析为沿 x 和 y 轴的水平和垂直分量。 $\vec{s}$沿这些轴的位移分量的大小为 x 和 y。速度$\vec{v}$分量的大小为 v _x = vcos$\theta$ 和 v _y = vsin$\theta$，其中 v 是速度的大小，$\theta$是其相对于速度的方向水平，如图所示$\PageIndex{2}$。
将运动视为两个独立的一维运动：一个是水平运动，另一个是垂直运动。使用前面介绍的运动学方程进行水平和垂直运动。
用两个单独的运动求解未知数：一个是水平的，一个是垂直的。请注意，运动之间唯一的常见变量是时间 t。此处的问题解决过程与一维运动学的解决过程相同，并在以下已解决的示例中进行了说明。
重新组合水平和垂直方向上的数量以找出总位移$\vec{s}$和速度$\vec{v}$。使用 $$s =\ sqrt {x^ {2} + y^ {2}}\ ldotp\ quad\ phi =\ tan^ {-1}\ 左 (\ dfrac {y} {x}\ 右)，\ quad v =\ sqrt {v_ {x} ^ {2} + v_ {y} ^ {2}}\ ldot tp$$where$\phi$ 是位移的方向$\vec{s}$。

图 a 显示了射弹在 x y 坐标系上 10 个时刻的位置和速度。当弹丸位于原点时，它的速度为 v sub 0 y，它与水平方向形成一个角度 theta sub 0。速度显示为深蓝色箭头，其 x 和 y 分量显示为浅蓝色箭头。弹丸的位置遵循向下打开的抛物线，向上移动到最大高度，然后返回 y = 0，然后继续低于 x 轴。速度 V 每次都会产生一个随时间变化的角度 theta，并有 x 分量 V sub x 和 y 分量 v sub y。速度 V sub x 的 x 分量在任何时候都是一样的。 y 分量 v sub y 指向上但会变小，直到弹丸达到最大高度，其中速度是水平的，没有 y 分量。达到最大高度后，速度会有一个 y 分量指向下并变大。当弹丸在向下途中达到与向上行驶时相同的高度时，其速度在水平线以下的角度与向上时在水平线上方的速度相同。特别是，当它在向下路上回到 y = 0 时，向量 v 和水平之间的角度为负 s=theta sub zero，速度的 y 分量为负 v sub 0 y。显示的最后一个位置在 x 轴下方，速度的 y 分量大于最初的位置。该图清楚地表明，在每个时间间隔内行驶的水平距离是相等的，而垂直距离在向上行驶时减小，向下行驶时会增加。图 b 显示了水平分量，恒定速度。水平位置和射弹速度的 x 分量沿水平线显示。位置间隔均匀，速度的 x 分量都相同，指向右侧。图 c 显示了垂直分量，恒定加速度。射弹速度的垂直位置和 y 分量沿垂直线显示。在上升的路上，位置越来越靠近，然后在下跌的路上相距更远。速度的 y 分量最初指向上方，幅度减小，直到最大高度处的速度没有 y 分量。达到最大高度后，速度的 y 分量向下指向并增大幅度。图 d 显示，将图 b 和 c 的水平和垂直分量放在一起可以得出某一点的总速度。速度 V 的 x 分量为 V sub x，y 分量为 V sub y，并且与水平方向的角度为 theta。在所示的示例中，速度具有向下 y 分量。 — 图$\PageIndex{2}$：（a）我们通过将二维弹丸沿垂直和水平轴分解为两个独立的一维运动来分析二维射弹运动。 (b) 水平运动很简单，因为 a _x = 0 而 v _x 是一个常数。 (c) 随着物体的升高，垂直方向的速度开始降低。在最高点，垂直速度为零。当物体再次落向地球时，垂直速度的幅度再次增加，但指向的方向与初始垂直速度相反。 (d) 重组 x 和 y 运动，以得出轨迹上任何给定点的总速度。

示例 4.7：一枚烟花弹在高处爆炸然后离开

在烟花汇演期间，炮弹以 70.0 m/s 的初始速度向空中射出，其角度高于水平线 75.0°，如图所示$\PageIndex{3}$。当炮弹到达地面上的最高点时，保险丝定时点燃炮弹。 (a) 计算炮弹爆炸的高度。 (b) 从炮弹发射到爆炸之间经过了多长时间？ (c) 炮弹爆炸时的水平位移是多少？ (d) 从发射点到最高点的总排水量是多少？

烟花炮弹从发射到最高点的轨迹在 y 图中显示为向下开口抛物线的左半部分，作为 x 的函数。最大高度为 h = 233 米，其当时的 x 位移为 x = 125 米。初始速度矢量 v sub 0 向上和向右，与轨迹曲线相切，并使 theta sub 0 的角度等于 75 度。 — 图$\PageIndex{3}$：烟花炮弹的轨迹。引信设定在弹道上的最高点爆炸炮弹，发现弹道高度为233米，水平距离为125米。

策略

运动可以分为水平和垂直运动，其中 a _x = 0，a _y = −g。然后我们可以将 x _{0 和} y ₀ 定义为零并求解所需的量。

解决方案

“高度” 是指起点上方的海拔或垂直位置 y。当 v _y = 0 时，将达到任何轨迹中的最高点，称为顶点。既然我们知道初始速度和最终速度以及初始位置，所以我们使用以下方程来找出 y：$$v_ {y} ^ {2} = v_ {0y} ^ {2} ^ {2} (y-y_ {0})\ ldotp$因_{为 y 0 和} v _y 都为零，方程简化为 $0 = v_ {0y} ^ {2} -2gy\ ldotp$solding for y 给 $$y=\ frac {v_ {0y} ^ {2}} {2g}\ ldotp$now 我们必须找到 v _0y，即 y 方向上初始速度的分量。它由 v _0y = v ₀ sin 给出$\theta_{0}$，其中 v ₀ 是 70.0 m/s 的初始速度，$\theta_{0}$= 75° 是初始角度。因此 $$v_ {0y} = v_ {0}\ sin\ theta = (70.0\; m/s)\ sin 75^ {o} = 67.6\; m/s$$and y 是 $$y =\ frac {(67.6\; m/s) ^ {2}} {2 (9.80\; m/s^ {2})}\ ldotp$thus，我们有 $$y = 233\; m\ ldotp$$注意，因为向上为正，所以初始垂直速度为正，最大高度也是如此，但由此产生的加速度来自重力是负的。另请注意，最大高度仅取决于初始速度的垂直分量，因此任何初始垂直速度分量为 67.6 m/s 的弹丸的最大高度均为 233 m（忽略空气阻力）。此示例中的数字对于大型烟花汇演是合理的，其炮弹在爆炸之前确实达到了这样的高度。实际上，空气阻力并非完全可以忽略不计，因此初始速度必须比给定的速度稍大一点才能达到相同的高度。
与许多物理问题一样，当弹丸达到最高点时，有不止一种方法可以求解。在这种情况下，最简单的方法是使用 v _y = v _0y − gt。因为顶点处的 v _y = 0，所以这个方程减少了 $0 = v_ {0y}-gt$$or $$t =\ frac {v_ {0y}} {g} =\ frac {67.6\; m/s} {9.80\; m/s^ {2}} = 6.90\; s\ ldotp$$这次对于大型烟花来说也是合理的。如果你能看到烟花的发射，请注意炮弹爆炸需要几秒钟。找到时间的另一种方法是使用 y = y ₀ +$\frac{1}{2}$ (v _0y + v _y) t。这个练习留给你完成。
由于空气阻力可以忽略不计，因此 a _x = 0 并且水平速度恒定，如前所述。水平位移是水平速度乘以时间，由 x = x ₀ + v _x t 给出，其中 x ₀ 等于零。因此，$$x = v_ {x} t，$$where v _x 是速度的 x 分量，由 $$v_ {x} = v_ {0}\ cos\ theta = (70.0\; m/s)\ cos 75^ {o} = 18.1\; m/s\ ldotp$time t 表示两个动作相同，所以 x 是 $$x = (18.1\; m/s) (6.90\; s) = 125\; m\ ldotp$水平运动是恒定速度没有空气阻力。此处发现的水平位移可能有助于防止烟花碎片落在观众身上。当炮弹爆炸时，空气阻力会产生重大影响，许多碎片会落在正下方。
刚刚计算了位移的水平和垂直分量，所以这里只需要找到最高点位移的大小和方向：$$\ vec {s} = 125\ hat {i} + 233\ hat {j} $$|\ vec {s} | =\ sqrt {125^ {2} + 233^ {2}} = 264\; m$$$\ theta =\ tan^ {-1}\ 左 (\ dfrac {233} {125}\ right) = 61.8^ {o}\ ldotp$请注意，位移向量的角度小于初始发射角度。要了解原因，请查看图$\PageIndex{1}$，其中显示了朝向地面的轨迹曲率。在求解示例 4.7 (a) 时，当空气阻力可以忽略不计时，我们找到的 y 表达式对任何弹丸运动都有效。称最大高度 y = h。然后，$$h =\ frac {v_ {0y} ^ {2}} {2g}\ ldotp$这个方程定义了弹丸在其发射位置上方的最大高度，它仅取决于初始速度的垂直分量。

练习 4.3

岩石以 15.0 m/s 的速度水平抛出 100.0 m 高的悬崖。(a) 定义坐标系的原点。 (b) 哪个方程描述了水平运动？ (c) 哪些方程描述了垂直运动？ (d) 岩石在撞击点的速度是多少？

示例 4.8：计算射弹运动-网球运动员

一名网球运动员在亚瑟·阿什球场赢得一场比赛，并以 30 m/s 的速度将球击入看台，与水平线高出 45° 的角度（图$\PageIndex{4}$）。在向下的路上，球被击球点上方 10 米处的旁观者抓住。 (a) 计算网球到达观众手中所需的时间。 (b) 球撞击时速度的大小和方向是多少？

一幅网球射入看台的插图。玩家在看台的左边，以 theta 的角度向上和向右击球，等于 45 度，v sub 0 的速度等于每秒 30 米。球到达坐在比球初始高度高出 10 米处的观众手中。 — 图$\PageIndex{4}$：网球击中看台的轨迹。

策略

同样，将这个二维运动解析为两个独立的一维运动使我们能够求解所需的量。弹丸在空中的时间仅由其垂直运动决定。因此，我们首先求解 t。当球垂直上升和下降时，水平运动以恒定速度继续。此示例要求输入最终速度。因此，我们将垂直和水平结果重新组合在一起，以获得$\vec{v}$在示例第一部分中确定的最终时间 t。

解决方案

当球在空中时，它会升起，然后下降到比起始高度高出 10.0 米的最终位置。我们可以使用方程式\ ref {4.22} 来找到时间：$$y = y_ {0} + v_ {0y} t-\ frac {1} {2} gt^ {2}\ ldotp$如果我们将初始位置 y ₀ 设为零，则最终位置为 y = 10 m。初始垂直速度是初始速度的垂直分量：$$v_ {0y} = v_ {0}\ sin\theta_ {0} = (30.0\; m/s)\ sin 45^ {o} = 21.2\; m/s\ ldotp$$用方程\ ref {4.22} 替换 y 会给我们 $10.0\; m = (21.2\; m/s^ {2}) t^ {2}\ ldotp$$reArranging 项给出二次方程 t 中的方程：$$ (4.90\; m/s^ {2}) t^ {2} − (21.2\; m/s) t + 10.0\; m = 0\ ldotp$使用二次公式产生 t = 3.79 秒，t = 0.54 秒。由于球在其轨迹中两次处于 10 m 的高度（一次在向上，一次在向下），因此我们对球到达旁观者所需的时间采用更长的解：$$t = 3.79\; s\ ldotp$射弹运动的时间完全确定通过垂直运动。因此，任何初始垂直速度为 21.2 m/s 且落在起始高度以上 10.0 m 的弹丸在空中停留 3.79 秒。
我们可以使用 (a) 的结果找到最终的水平和垂直速度 v _x 和 v _y。然后，我们可以将它们组合起来，得出总速度矢量的大小$\vec{v}$以及$\theta$它与水平方向的角度。由于 v _x 是恒定的，我们可以在任何水平位置对其进行求解。之所以选择起点，是因为我们知道初始速度和初始角度。因此，$$v_ {x} = v_ {0}\ cos\ theta_ {0} = (30\; m/s)\ cos 45^ {o} = 21.2\; m/s\ ldotp$$最终垂直速度由方程\ ref {4.21} 给出：$$v_ {y} = v_ {0y} − gt\ ldotp$since 存在$v_{0y}$于 (a) 要达到 21.2 m/s，我们有 $$v_ {y} = 21.2\; m/s − (9.8\; m/s^ {2}) (3.79 秒) = −15.9\; m/s\ ldotp$$最终速度的大小$\vec{v}$为 $$v =\ sqrt {v_ {x} ^ {2} + v_ {y} ^ {2}} =\ sqrt {(21.2\; m/s) ^ {2} + (-15.9\; m/s) ^ {2}} = 26.5\; m/s\ ldotp$方向$\theta_{v}$是使用反切线找到的：$$\ theta_ {v} =\ tan^ {-1}\ 左 (\ dfrac {v_ {y}} {v_ {x}}\ 右) =\ tan^ {-1}\ 左 (\ dfrac {21.2} {-15.9}\右) = -53.1^ {o}\ ldotp$$

意义

如前所述，射弹运动的时间完全由垂直运动决定。因此，任何初始垂直速度为 21.2 m/s 且落在起始高度以上 10.0 m 的弹丸在空中停留 3.79 秒。
负角度表示撞击点的速度比水平线低 53.1°。该结果与以下事实一致：球在轨迹顶点另一侧的某个点撞击，因此速度的 y 分量为负。速度的大小于我们预期的初始速度的大小，因为它撞击了发射高度上方10.0 m。

飞行时间、轨迹和航程

有趣的是射弹在平坦的水平表面发射并撞击同一表面的飞行时间、轨迹和射程。在这种情况下，运动学方程为这些量提供了有用的表达式，这些表达式将在以下各节中推导。

飞行时间

通过对运动学方程进行一些操作，我们可以求解既发射又撞击平坦水平表面的弹丸的飞行时间。我们注意到，在发射和撞击平坦表面时，y 中的位置和位移必须为零。因此，我们将y中的位移设置为零并找到

\[y − y_{0} = v_{0y} t − \frac{1}{2} gt^{2} = (v_{0} \sin \theta_{0})t − \frac{1}{2} gt^{2} = 0 \ldotp\]

保理，我们有

\[t \left(v_{0} \sin \theta_{0} - \dfrac{gt}{2}\right) = 0 \ldotp\]

求解 t 可以给我们带来好处

\[T_{tof} = \frac{2(v_{0} \sin \theta_{0})}{g} \ldotp \label{4.24}\]

这是弹丸在平坦的水平表面发射和撞击的飞行时间。方程式\ ref {4.24} 不适用于弹丸降落在与发射高度不同的高度，如我们在示例 4.8 中看到的网球运动员将球击入看台。另一个解 t = 0 对应于发射时间。飞行时间与 y 方向的初始速度成线性成正比，与 g 成反比。因此，在重力为地球六分之一的月球上，以与地球相同速度发射的弹丸的空中飞行时间将是地球的六倍。

轨迹

弹丸的轨迹可以通过从任意 t 的运动学方程中消除时间变量 t 并求解 y (x) 来找出。我们采用 x ₀ = y ₀ = 0 所以弹丸是从原点发射的。 x 的运动学方程给出

\[x = v_{0x}t \Rightarrow t = \frac{x}{v_{0x}} = \frac{x}{v_{0} \cos \theta_{0}} \ldotp\]

将 t 的表达式代入位置 y = (v ₀ sin$\theta_{0}$) t −$\frac{1}{2}$ gt ² 的方程中得出

\[y = (v_{0} \sin \theta_{0}) \left(\dfrac{x}{v_{0} \cos \theta_{0}}\right) - \frac{1}{2} g \left(\dfrac{x}{v_{0} \cos \theta_{0}}\right)^{2} \ldotp\]

重新排列条款，我们有

\[y = (\tan \theta_{0})x - \Big[ \frac{g}{2(v_{0} \cos \theta_{0})^{2}} \Big] x^{2} \ldotp \label{4.25}\]

这个轨迹方程的形式为 y = ax + bx ²，这是一个带有系数的抛物线方程

\[a = \tan \theta_{0}, \quad b = - \frac{g}{2(v_{0} \cos \theta_{0})^{2}} \ldotp\]

射程

从弹道方程中，我们还可以找到射程或弹丸行进的水平距离。分解方程\ ref {4.25}，我们有

\[y = x \Big[ \tan \theta_{0} - \frac{g}{2(v_{0} \cos \theta_{0})^{2}} x \Big] \ldotp\]

发射点和撞击点的位置y均为零，因为我们再次考虑的只是平坦的水平表面。在此方程中设置 y = 0 可得出解 x = 0，对应于发射点，并且

\[x = \frac{2 v_{0}^{2} \sin \theta_{0} \cos \theta_{0}}{g} ,\]

对应于撞击点。使用三角恒等式 2sin$\theta$ cos$\theta$ = sin2$\theta$ 并将 x = R 设置为范围，我们发现

\[R = \frac{v_{0}^{2} \sin 2 \theta_{0}}{g} \ldotp \label{4.26}\]

特别注意方程\ ref {4.26} 仅对水平表面的发射和撞击有效。我们看到该范围与初始速度 v _{0 和} sin ² 的平方成正比$\theta_{0}$，并且与重力加速度成反比。因此，在相同的初始速度下，在月球上，射程将比地球上的射程大六倍。此外，我们从因子 sin ² 中$\theta_{0}$可以看出，最大范围为 45°。这些结果如图所示$\PageIndex{5}$。在 (a) 中，我们可以看到初始速度越大，范围越大。在 (b) 中，我们可以看到最大范围为 45°。只有在忽视空气阻力的条件下才是如此。如果考虑空气阻力，则最大角度会稍小一些。有趣的是，两个初始发射角度的射程相同，总和为90°。以较小角度发射的弹丸的顶点低于较高角度，但它们的射程相同。

图 a 显示了以与水平线上方相同的 45 度角和不同的初始速度发射的射弹的轨迹。显示了从发射到着陆的初始海拔高度处的轨迹。橙色表示每秒 30 米的轨迹，射程 R（从发射到着陆的距离）为 91.8 m。紫色表示每秒 40 米的轨迹，射程 R 为 163 m。蓝色是每秒 50 米的轨迹，射程 R 为 255 m。弹丸的最大高度随着初始速度的增加而增加。图 b 显示了以相同初始速度（每秒 50 米）和不同发射角度发射的射弹的轨迹。显示了从发射到着陆的初始海拔高度处的轨迹。橙色表示角度高于水平线 15 度的轨迹，给出范围 R 为 128 m。紫色是距离水平线 45 度角的轨迹，给出 255 m 的范围 R 的轨迹。蓝色是距离水平线 75 度的轨迹，给出 128 m 的范围 R与 15 度轨迹相同。最大高度随着发射角度的增加而增加。 — 图$\PageIndex{5}$：射弹在平坦地面上的轨迹。 (a) 初始速度 v ₀ 越大，给定初始角度的范围越大。 (b) 初始角度 (\ theta_ {0}\) 对给定初始速度的弹丸射程的影响。请注意，初始角度 15° 和 75° 的范围相同，尽管这些路径的最大高度不同。

示例 4.9：比较高尔夫球杆

高尔夫球手在不同的洞里发现自己处于两种不同的境地。在第二个洞中，他距离果岭 120 米，他想将球击中 90 米，然后让球跑到果岭上。他将射门偏低到地面，与水平方向成30°，让球在撞击后滚动。在第四洞他距离果岭 90 米，他想让球在撞击后以最少的滚动量掉落。在这里，他将射门与水平方向成70°的角度，以最大限度地减少撞击后的滚动。两枪都被击中并撞击在水平表面上。 (a) 第二洞球的初始速度是多少？ (b) 第四洞球的初始速度是多少？ (c) 写下两种情况的轨迹方程。 (d) 绘制轨迹图。

策略

我们看到范围方程具有初始速度和角度，因此我们可以求解 (a) 和 (b) 的初始速度。当我们有了初始速度时，我们可以使用这个值来写出轨迹方程。

解决方案

$$R =\ frac {v_ {0} ^ {2}\ sin 2\ theta_ {0}} {g}\ Rightarrow v_ {0} =\ sqrt {\ dfrac {Rg} {\ sqrt {\ dfrac {(90.0\; m) (9.8\; m/s^ {2})} {\ sin (2 (30^ {o})}} = 31.9\; m/s$$
$$R =\ frac {v_ {0} ^ {2}\ sin 2\ theta_ {0}} {g}\ Rightarrow v_ {0} =\ sqrt {\ dfrac {Rg} {\ sqrt {\ dfrac {(90.0\; m) (9.8\; m/s^ {2})} {\ sin (2 (70^ {o})}} = 37.0\; m/s$$
$$y = x\ Big [\ tan\ theta_ {0}-\ frac {g} {2 (v_ {0}\ cos\ theta_ {0}) ^ {2}} x\ Big] $$Second Hole：$$y = x\ Big [\ tan 30^ {o}-\ frac {9.8\; m/s^ {2}} {2\; m/s) (\ cos 30^ {o})] ^ {2}} x\ Big] = 0.58x-0.0064x^ {2} $$第四洞：$$y = x\ Big [\ tan 70^ {o}-\ frac {9.8\; m/s {2}} {2 [(37.0\; m/s) (\ cos 70^ {o})] {^ 2} x\ Big] = 2.75x-0.0306x^ {2} $$
使用绘图实用程序，我们可以比较两个轨迹，如图所示$\PageIndex{6}$。

显示了两个抛物线函数。两条轨迹的射程均为 90 米。一枪的射程比另一枪高得多。较高的射击的初始速度为每秒 37 米，角度为 70 度。较低的射击的初始速度为每秒 31.9 米，角度为 30 度。 — 图$\PageIndex{6}$：射程为 90 米的高尔夫球的两条轨迹。两者的撞击点与发射点处于同一高度。

意义

70° 射击的初始速度大于 30° 时射击的初始速度。从图中可以看出，如果发射角度增加$\PageIndex{6}$到 90°，则两枚射弹以相同速度但以不同角度发射的射程相同。本示例中的发射角度相加得出一个大于 90° 的数字。因此，70° 的射击必须具有更高的发射速度才能达到 90 m，否则它将以更短的距离着陆。

练习 4.4

如果示例 4.9 中的两个高尔夫球以相同的速度发射，那么哪个射门的射程最大？

当我们谈到射弹在平地上的射程时，我们假设 R 与地球周长相比非常小。但是，如果射程很大，则地球会弯曲到弹丸下方，重力产生的加速度会沿路径改变方向。射程比前面给出的射程方程预测的要大，因为弹丸的掉落距离要比在水平地面上落得更远，如图所示$\PageIndex{7}$，该图是根据牛顿的 Princ ipia 绘制的。如果初始速度足够快，则弹丸进入轨道。地球表面每 8000 米下降 5 米。在 1 秒内，一个物体在没有空气阻力的情况下坠落 5 米。因此，如果给定一个物体在地球表面附近的水平速度为8000 m/s（或18,000 mi/hr），它将进入环绕地球的轨道，因为该物体表面会不断脱离该物体。这大致相当于航天飞机运行时在低地球轨道上的速度，或任何低地球轨道上的卫星的速度。 Gravitat ion 更深入地涵盖了轨道运动的这些方面和其他方面，例如地球的自转。

该图显示了一幅地球图，北极有一座高塔，标有 v 0 的水平箭头指向右边。显示了从塔顶开始的 5 条轨迹。第一个到达塔附近的地球。第二个到达离塔更远的地球，第三个到达更远的地球。第四条轨迹在赤道撞击地球，与赤道的表面相切。第五条轨迹是与地球同心的圆。 — 图$\PageIndex{7}$：射弹到卫星。在此处显示的每种情况下，弹丸都是从非常高的塔上发射的，以避开空中阻力。随着初始速度的提高，射程会增加，变得比在平坦的地面上更长，因为地球会在其路径下方弯曲。在 8000 m/s 的速度下，轨道就实现了。

模拟

在 PhET Explorations：弹丸运动中，从发射角度和初始速度的角度了解弹丸运动。