2.3: 标量和向量（第 2 部分）

Last updated
Save as PDF

Page ID: 204392

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

示例\(\PageIndex{1}\): A Ladybug Walker

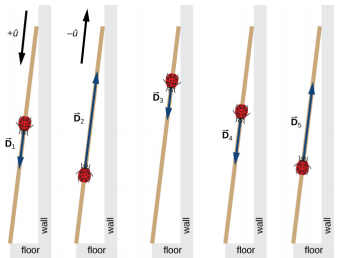
在物理实验室里，一根长量尺靠在墙上，其末端在地板上 200 厘米。一只瓢虫落在 100 厘米的标记处，然后沿着棍子随机爬行。它首先向地板走 15 厘米，然后向墙移动 56 厘米，然后再次向地板移动 3 厘米。然后，在短暂停留后，它继续向地板行驶 25 厘米，然后再次向墙向上爬行 19 厘米，然后完全休息（图\(\PageIndex{1}\)）。找到其总位移量及其在摇杆上最终静止位置的向量。

策略

如果我们选择沿着棍子朝向地板的方向作为单位向量的方向\(\hat{u}\)，那么朝向地板的方向是\(+ \hat{u}\)，朝向墙的方向是\(−\hat{u}\)。瓢虫总共会产生五次位移：

\[ \begin{align*} \vec{D}_{1} &= (15\; cm)( + \hat{u}), \\[4pt] \vec{D}_{2} &= (56\; cm)( - \hat{u}), \\[4pt] \vec{D}_{3} &= (3\; cm)( + \hat{u}), \\[4pt] \vec{D}_{4} &= (25\; cm)( + \hat{u}), \; and \\[4pt] \vec{D}_{5} &= (19\; cm)( - \hat{u}) \ldotp \end{align*}\]

总位移\(\vec{D}\)是其所有位移向量的结果。

五幅插图，描绘的是尺子上的一只瓢虫靠在墙上。 +u 帽子方向朝向平行于标尺的地面，而 — u hat 方向沿着标尺向上。在第一幅插图中，瓢虫位于标尺中间附近，向量 D sub 1 指向标尺的下方。在第二幅插图中，瓢虫位于下方，其中向量 D sub 1 的头部在第一幅插图中，向量 D sub 2 指向标尺的上方。在第三幅插图中，瓢虫位于较高位置，其中向量 D sub 2 的头部在第二个插图中，向量 D sub 3 指向标尺的下方。在第四幅插图中，瓢虫位于下方，其中向量 D sub 3 的头部在第三幅插图中，向量 D sub 4 指向标尺的下方。在第五幅插图中，瓢虫位于下方，其中向量 D sub 4 的头部在第四幅插图中，向量 D sub 5 指向标尺的上方。 — 图\(\PageIndex{1}\)：瓢虫的五次位移。请注意，在这张示意图中，位移量不是按比例绘制的。（来源：“波斯诗人 Gal” /Wikimedia Commons 对作品的修改）

解决方案

所有位移向量的结果是

\[ \begin{align*} \vec{D} &= \vec{D}_{1} + \vec{D}_{2} + \vec{D}_{3} + \vec{D}_{4} + \vec{D}_{5} \\[4pt] &= (15\; cm)( + \hat{u} ) + (56\; cm)( −\hat{u} ) + (3\; cm)( + \hat{u} ) + (25\; cm)( + \hat{u}) + (19\; cm)( − \hat{u}) \\[4pt] &= (15 − 56 + 3 + 25 − 19) cm\; \hat{u} \\[4pt] &= −32\; cm\; \hat{u} \ldotp \end{align*}\]

在此计算中，我们使用方程 2.2.9 给出的分布定律。结果显示，总位移向量指向 100 厘米标记（初始着陆点），指向接触墙壁的仪表杆的末端。接触墙壁的末端标记为 0 cm，因此瓢虫的最终位置是 (100 — 32) cm = 68 cm 标记。

练习 2.2

一名洞穴潜水员进入一条长长的水下隧道。当她相对于入口点的位移为 20 米时，她不小心掉下了相机，但直到距离隧道大约 6 米处她才注意到相机丢失了。她向后游了 10 米，但找不到相机，所以她决定结束潜水。她离入口有多远？从隧道中取出正方向，她相对于入口点的位移向量是多少？

二维向量代数

当向量位于平面上时（即当它们处于二维状态时），可以按照方程 2.2.1、方程 2.. 2. 2、方程 2.2.7 和方程 2.2.8。但是，平面中两个向量的加法规则变得比一维向量加法规则更为复杂。我们必须使用几何定律来构造合成向量，然后使用三角学来找到向量大小和方向。这种几何方法通常用于导航（图\(\PageIndex{2}\)）。在本节中，我们需要手头有两个标尺，一个三角形，一个量角器，一支铅笔和一个橡皮擦，用于绘制按几何结构缩放的矢量。

有人用卡尺和尺子在地图上测量距离的照片。 — 图\(\PageIndex{2}\)：在导航中，几何定律用于在航海地图上绘制由此产生的位移。

对于平面中两个向量之和的几何构造，我们遵循平行四边形规则。假设两个向量\(\vec{A}\)和\(\vec{B}\)位于图中所示的任意位置\(\PageIndex{3}\)。平移其中一个向量与另一个向量的开头平行，这样在平移之后，两个向量的起点都位于同一点。现在，在向量的末尾\(\vec{A}\)我们画一条平行于向量的\(\vec{B}\)直线，在向量的\(\vec{B}\)末尾绘制一条平行于向量的直线\(\vec{A}\)（图中的虚线\(\PageIndex{3}\)）。通过这种方式，我们可以得到一个平行四边形。我们从两个向量的原点绘制一条对角线，该对角线是两个向量的结果\(\vec{R}\)：\(\vec{R}\)=\(\vec{A}\) +\(\vec{B}\)（图\(\PageIndex{3a}\)）。这个平行四边形的另一个对角线是两个向量的向量差\(\vec{D}\) =\(\vec{A}\) −\(\vec{B}\)，如图所示\(\PageIndex{3b}\)。请注意，差值向量的末端放置在向量的末端\(\vec{A}\)。

图示了添加向量的平行四边形方法。在图 a 中，显示了向量 A 和 B。向量 A 指向右和向下，向量 B 指向右和向上。然后，向量 A 和 B 显示为实心箭头，它们的尾巴在一起，方向与以前一样。显示了一条平行于矢量 A 但已移位的虚线，因此它从 B 的头部开始。还显示了第二条虚线，该虚线平行于 B，起始于 A 的头部。向量 A 和 B 以及两条虚线形成平行四边形。显示了第三个向量，即标记向量 R = 向量 A 加上向量 B。向量 R 的尾部位于向量 A 和 B 的尾部，矢量 R 的头部是虚线在平行四边形上相互交汇的地方。我们注意到 R 的大小不等于 A 的大小加上 B 的大小。在图 b 中，显示了向量 A 和减去 B。向量减去 B 是来自零件 a 的向量 B，旋转 180 度。向量 A 指向右和向下，向量减去 B 指向左和向下。然后，向量 A 和 B 显示为实心箭头，它们的尾巴在一起，方向与以前一样。显示了一条平行于矢量 A 但已移位的虚线，因此它从 B 的头部开始。还显示了第二条虚线，该虚线平行于 B，起始于 A 的头部。向量 A 和 B 以及两条虚线形成平行四边形。显示了第三个向量，即标记向量 D。向量 D 的尾部位于向量 B 的开头，向量 D 的头部位于向量 A 的开头，沿对角线穿过平行四边形。我们注意到向量 D 等于向量 A 减去向量 B，但是 D 的大小不等于 A 减去 B 的幅度。 — 图\(\PageIndex{3}\)：两个向量相加的平行四边形规则。将每个向量平行平移到其原点（用点标记）重合的点，然后构造一个平行四边形，其两边在向量上，另外两边（用虚线表示）与向量平行。 (a)\(\vec{R}\) 沿平行四边形的对角线从公共点到对角线绘制合成的向量。合成向量的长度 R 不等于两个向量的大小之和。 (b)\(\vec{B}\) 沿着连接向量两端的对角线绘制差向量\(\vec{D}\) =\(\vec{A}\) −。将向量的原\(\vec{D}\)点放在向量的末尾\(\vec{B}\)，将向量的末尾（箭头）放在向\(\vec{D}\)量的末尾\(\vec{A}\)。差值向量的长度 D 不等于两个向量的量级差。

根据平行四边形规则，合成向量的大小和差值向量都不能表示为量级 A 和 B 的简单总和或差，因为对角线的长度不能表示为边长的简单总和。当使用几何结构来查找量级 |\(\vec{R}\) | 和\(\vec{D}\) | 时，我们必须对三角形使用三角定律，这可能会导致复杂的代数。有两种方法可以规避这种代数复杂性。一种方法是使用组件方法，我们将在下一节中对此进行研究。另一种方法是按比例绘制向量，就像在导航中一样，然后从图表中读取近似的矢量长度和角度（方向）。在本节中，我们将研究第二种方法。

如果我们需要添加三个或更多向量，则对向量对重复平行四边形规则，直到找到所有结果的结果为止。例如，对于三个向量，我们首先找到向量 1 和向量 2 的合成，然后找到该合成和向量 3 的合成。我们选择向量对的顺序并不重要，因为向量加法的运算是可交换和关联的（参见方程 2.2.7 和方程 2.2.8）。在我们陈述重复应用平行四边形规则所产生的一般规则之前，让我们看下面的示例。

假设你计划在佛罗里达度假旅行。从州首府塔拉哈西出发，你计划去杰克逊维尔拜访你的叔叔乔，在代托纳比奇见你的堂兄 Vinny，在奥兰多停下来玩一会儿，在坦帕看马戏表演，然后参观盖恩斯维尔的佛罗里达大学。您的路径可以用五个位移向量\(\vec{A}\)\(\vec{B}\)、\(\vec{C}\)\(\vec{D}\)\(\vec{E}\)、和表示，它们由图中的红色向量表示\(\PageIndex{4}\)。当你到达盖恩斯维尔时，你的总排水量是多少？总位移是所有五个位移向量的矢量总和，可以通过使用四次平行四边形规则得到。或者，回想一下，位移向量的起点是初始位置（塔拉哈西），终点是最终位置（盖恩斯维尔），因此总位移向量可以直接绘制为连接塔拉哈西和盖恩斯维尔的箭头（见图中的绿色向量\(\PageIndex{4}\)）。当我们四次使用平行四边形规则时，\(\vec{R}\)我们得到的结果正是连接塔拉哈西和盖恩斯维尔的绿色向量：\(\vec{R}\)=\(\vec{A}\)\(\vec{B}\) +\(\vec{C}\) +\(\vec{D}\) +\(\vec{E}\)。

佛罗里达地图，以下矢量以红色显示：从塔拉哈西到杰克逊维尔的矢量 A，差不多在西边。 Vector B 从杰克逊维尔到东南部的代托纳比奇。从代托纳比奇到西南奥兰多的矢量 C。从奥兰多到西南坦帕的向量 D（但垂直度小于矢量 C）。 Vector E 从坦帕到盖恩斯维尔，稍微在北部以东。从塔拉哈西到盖恩斯维尔的矢量 R 显示为绿色箭头。 — 图\(\PageIndex{4}\)：当我们四次使用平行四边形规则时，我们得到的结果向量\(\vec{R}\) =\(\vec{A}\) +\(\vec{B}\) +\(\vec{C}\) +\(\vec{D}\) +\(\vec{E}\)，这是连接塔拉哈西和盖恩斯维尔的绿色向量。

使用以下尾对头几何结构可以对绘制许多向量的合成向量进行概括。假设我们要绘制由四个向量\(\vec{R}\)\(\vec{A}\)、\(\vec{B}\)\(\vec{C}\)、和\(\vec{D}\)（图\(\PageIndex{5a}\)）组成的合成向量。我们选择其中任何一个向量作为第一个向量，然后将第二个向量平行平移到第二个向量的原点（“尾部”）与第一个向量的末端（“头”）重合的位置。然后，我们选择第三个向量，将第三个向量平行平移到第三个向量的原点与第二个向量的末端重合的位置。我们重复此过程，直到所有向量都采用从头到尾的排列方式，如图所示\(\PageIndex{5}\)。我们\(\vec{R}\)通过将第一个向量的原点（“尾部”）与最后一个向量的末端（“头部”）连接来绘制合成向量。合成向量的末尾位于最后一个向量的末尾。由于向量的加法是关联和可交换的，因此无论我们在此构造中选择哪个向量作为第一、第二、第三或第四个向量，我们都会获得相同的结果向量。

在图 a 中，分别显示了标记为 A、B、C 和 D 的四个向量。在图 b 中，向量从头到尾排列：向量 A 的尾巴位于 D 的头部。向量 C 的尾巴在 A 的头部，向量 B 的尾部位于 C 的头部。每个向量指向的方向与图 a 中的方向相同。第五个向量 R 从向量 D 的尾部开始，结束于向量 B. — 图\(\PageIndex{5}\)：绘制合成向量的尾对头方法\(\vec{R}\) =\(\vec{A}\) +\(\vec{B}\) +\(\vec{C}\) +\(\vec{D}\)。 (a) 四个不同大小和方向的向量。 (b) (a) 中的向量被平移到新的位置，其中一个向量的原点（“尾部”）位于另一个向量的末端（“头”）。在此排列中，生成的向量从第一个向量的原点（“尾部”）绘制到最后一个向量的末端（“头”）。

示例\(\PageIndex{2}\): Geometric Construction of the Resultant

图\(\vec{C}\)\(\PageIndex{6}\)中的三个位移向量\(\vec{A}\)\(\vec{B}\)、和分别由其幅度 A = 10.0、B = 7.0 和 C = 8.0 指定，以及它们各自的方向角指定，水平方向\(\alpha\) = 35°、\(\beta\) = −110° 和\(\gamma\) = 30°。量级的物理单位是厘米。选择一个方便的刻度并使用标尺和量角器求出以下矢量和：(a)\(\vec{R}\) =\(\vec{A}\) +\(\vec{B}\)、(b)\(\vec{D}\) =\(\vec{A}\) −\(\vec{B}\) 和 (c)\(\vec{S}\) =\(\vec{A}\) −\(3 \vec{B}\) +\(\vec{C}\)。

向量 A 的幅度为 10.0，与水平方向成了 alpha = 35 度的角度。它指向上和向右。向量 B 的幅度为 7.0，与水平方向的角度 beta = -110 度顺时针方向。它指向下和向左。向量 C 的幅度为 8.0，与水平方向成伽玛 = 30 度的角度。它指向上和向右。向量 F 的幅度为 20.0，与水平方向成了 phi = 110 度的角度。它指向上和向左。 — 图\(\PageIndex{6}\)：示例\(\PageIndex{2}\)和随后的练习功能中使用的向量。

策略

在几何构造中，找到矢量意味着找到其大小及其与水平方向的方向角度。策略是绘制以缩放出现在方程右侧的向量，然后构造合成的向量。然后，使用尺子和量角器读取合成物的大小和方向角。对于 (a) 和 (b) 部件，我们使用平行四边形规则。对于 (c)，我们使用尾对头方法。

解决方案

对于 (a) 和 (b) 部分，我们将向量的原点附加\(\vec{B}\)到向量的原点\(\vec{A}\)，如图所示\(\PageIndex{7}\)，然后构造一个平行四边形。这个平行四边形的较短对角线是总和\(\vec{A}\) +\(\vec{B}\)。对角线越长就是差异\(\vec{A}\) −\(\vec{B}\)。我们用尺子测量对角线的长度，用量角器测量水平角度。对于由此得出的结果\(\vec{R}\)，我们得到 R = 5.8 cm\(\theta_{R}\) 和 β 0°。为了实现差异\(\vec{D}\)，我们得到 D = 16.2 cm 和\(\theta_{D}\) = 49.3°，如图所示\(\PageIndex{7}\)。

向量 A 和 B 的三张图显示了向量 A 和 B 从头到尾放置。向量 A 指向上和向右，幅度为 10.0。向量 B 指向下和向左，幅度为 7.0。向量 A 和 B 之间的角度为 145 度。在第二张图中，再次显示了向量 A 和 B 以及完成平行四边形的虚线。等于向量 A 和 B 之和的向量 R 显示为从 A 和 B 尾部到平行四边形相对顶点的向量。 R 的大小为 5.8。在第三张图中，再次显示了向量 A 和 B 以及完成平行四边形的虚线。等于向量 A 和 B 之差的向量 D 显示为从 B 的头部到 A 头部的向量。D 的大小为 16.2，D 和水平之间的角度为 49.3 度。第二张图中的向量 R 比第三张图中的向量 D 短得多。 — 图\(\PageIndex{7}\)：使用平行四边形规则求解 (a)（找到结果，红色）和（b）（求差，蓝色）。

对于 (c)，我们可以从向量 −3 开始，\(\vec{B}\)然后将剩余的向量从头到尾绘制，如图所示\(\PageIndex{8}\)。在向量加法中，我们绘制向量的顺序并不重要，但是按比例绘制向量非常重要。接下来，我们绘制\(\vec{S}\)从第一个向量的原点到最后一个向量的末尾的向量，并将箭头放在的末尾\(\vec{S}\)。我们用尺子测量长度\(\vec{S}\)，发现其大小为 S = 36.9 cm。我们使用量角器，发现它的方向角为\(\theta_{S}\) = 52.9°。该解决方案如图所示\(\PageIndex{8}\)。

三个向量以蓝色显示，从头到尾放置：向量减去 3 B 指向上和向右，大小为 3 B = 21.0。向量 A 从 B 的头部开始，指向上和向右，大小为 A=10.0。向量 A 和向量减去 3 B 之间的角度为 145 度。向量 C 从 A 的头部开始，其幅度为 C=8.0。向量 S 为绿色，从负 3 B 的尾部一直延伸到 C 的头部。向量 S 等于向量 A 减去 3 向量 B 加上向量 C，大小为 S=36.9，与水平方向逆时针成了 52.9 度的角度。 — 图\(\PageIndex{8}\)：使用尾对头方法求解 (c)（查找向量\(\vec{S}\)，绿色）。

练习 2.3

使用三个位移向量\(\vec{A}\)\(\vec{B}\)，然后\(\vec{F}\)在图\(\PageIndex{6}\)中选择一个方便的比例，然后使用标尺和量角器找到由矢量方程\(\vec{G}\) =\(\vec{A}\) +\(2 \vec{B}\) −\(\vec{G}\) 给出的向量\(\vec{F}\)。

模拟

通过访问这个向量计算器和这个 PhET 模拟，观察平面中向量的加法情况。