18.4: H-R 图

学习目标

在本节结束时，您将能够：

• 确定用于创建 H—R 图的恒星的物理特征，并描述这些特征在恒星组之间有何不同
• 讨论在 H—R 图上不同位置发现的大多数恒星的物理特性，例如半径；对于主序列恒星，则为 mas

在本章和《分析星光》中，我们描述了我们可以用来对恒星进行分类的一些特征以及如何测量这些特征。 表中总结了这些想法\(\PageIndex{1}\)。 我们还举了一个例子，说明质量-亮度关系中这两个特征之间的关系。 二十世纪初，当测量大量恒星的特征时，天文学家得以开始更深入地寻找这些数据中的模式和关系。

表\(\PageIndex{1}\)：测量恒星的特征

特点	技巧
表面温度	1。 确定颜色（非常粗糙）。 2。 测量光谱并获取光谱类型。
化学成分	确定频谱中存在哪些线。
亮度	测量视在亮度并补偿距离。
径向速度	测量频谱中的多普勒偏移。
旋转	测量光谱线的宽度。
弥撒	测量光谱双星的周期和径向速度曲线。
直径	1。 测量恒星的光线被月亮阻挡的方式。 2。 测量使双星黯然失色的光曲线和多普勒偏移。

为了帮助理解可能发现什么样的关系，让我们简要看一下有关人类的一系列数据。 如果你想通过比较和对比人类的特征来理解人类，而不必假设以前对这些奇怪的生物有任何了解，你可以尝试确定哪些特征会引导你朝着富有成效的方向前进。 例如，您可以根据人类体重（这是衡量其质量的指标）绘制大量人类样本的高度。 这样的图如图所示\(\PageIndex{1}\)，它具有一些有趣的特征。 在我们选择呈现数据的方式中，身高向上增加，而体重向左增加。 请注意，人类在图表中不是随机分布的。 大多数点落在从左上角到右下角的序列上。

身\(\PageIndex{1}\)高与体重。 代表性人类群体的身高和体重图。 大多数点位于代表大多数人的 “主序列” 上，但也有少数例外。

我们可以从这张图中得出结论，人的身高和体重是相关的。 一般来说，身高的人体重更重，而矮个子的人体重更轻。 如果你熟悉人类的结构，这是有道理的。 通常，如果我们有更大的骨头，我们就有更多的肉来填充更大的框架。 它在数学上并不精确——变化范围很广——但总体而言，这不是一个坏规则。 当然，也有一些引人注目的例外。 你偶尔会看到一个身材矮小的人，他超重得很重，因此比普通人群更在图表的左下角。 或者你可能有一个身材高大、瘦弱的时装模特，身高但体重相对较小，他会在右上角附近找到。

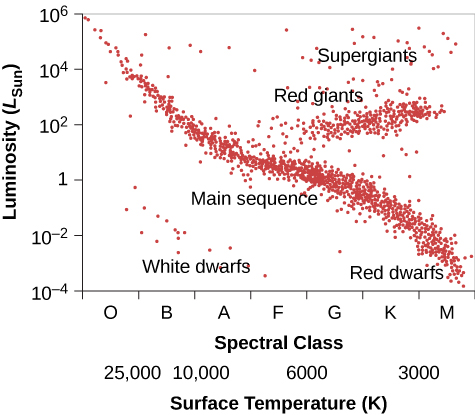
人们发现，类似的图表对于理解恒星的生命非常有用。 1913年，美国天文学家亨利·诺里斯·罗素（Henry Norris Russell）根据恒星的光谱等级（一种表示其表面温度的方法）绘制了恒星的亮度。 这项调查以及丹麦天文学家Ejnar Hertzsprung在1911年进行的一项类似的独立研究得出了一个极其重要的发现，即恒星的温度和亮度是相关的（图\(\PageIndex{2}\)）。

图\(\PageIndex{2}\) Hertzsprung（1873—1967）和罗素（1877—1957 年）。 (a) Ejnar Hertzsprung 和 (b) Henry Norris Russell 独立发现了恒星亮度与表面温度之间的关系，现在所谓的 H—R 图对此进行了总结。

亨利·诺里斯·罗素

亨利·诺里斯·罗素（Henry Norris Russell）从普林斯顿大学毕业时，他的工作非常出色，以至于教师决定为他创建一个新的荣誉学位，而不是 “优异成绩”。 他的学生后来想起他是一个思维速度比其他人快三倍的人。他的记忆力非常惊人，他可以正确地引用大量的诗歌和打油诗、整本圣经、数学函数表以及他所学到的关于天文学的几乎所有东西。 他很紧张、活跃、有竞争力、挑剔，而且口齿清晰；他倾向于在他参加的每次会议中占据主导地位。 从外表上看，他是十九世纪的老式产品，他穿着黑色高帮鞋子和高淀粉领，一生中每天都带着雨伞。 他的264篇论文在天文学的许多领域都具有巨大的影响力。

罗素出生于1877年，是长老会牧师的儿子，他表现出了早期的希望。 当他 12 岁时，他的家人派他去普林斯顿和一位姑姑住在一起，这样他就可以上一所顶尖的预科学校。 他一直住在那个城镇的同一所房子里，直到 1957 年去世（只是在欧洲短暂停留研究生工作才中断）。 他喜欢讲述自己的母亲和外祖母都曾获得过数学奖，而且他可能是从他们的家庭那里继承了他在该领域的才华。

在罗素之前，美国天文学家主要致力于调查恒星，并对恒星的特性进行令人印象深刻的目录，尤其是它们的光谱（如分析星光中所述）。 罗素开始认识到，解释恒星的光谱需要对原子的物理学有更深入的了解，这是欧洲物理学家在20世纪10年代和1920年代开发的主题。 罗素开始了终身探索，希望从恒星光谱中的线索中确定恒星内部的物理状况；他的工作启发并延续了一代天文学家，其中许多人是由罗素及其合作者训练的。

罗素还在研究双星和恒星质量测量、太阳系起源、行星大气层、天文学距离测量等领域做出了重要贡献。 他是一位有影响力的天文学老师和普及者，为《科学美国人》杂志撰写有关天文学主题的专栏文章已有40多年。 他和两位同事为大学天文学课写了一本教科书，几十年来帮助培训天文学家和天文学爱好者。 那本书为你现在正在阅读的那种教科书奠定了基础，它不仅列出了天文学的事实，还解释了它们是如何组合在一起的。 罗素在全国各地举办讲座，经常强调理解现代物理学对于掌握天文学正在发生的事情的重要性。

哈佛大学天文台主任哈洛·沙普利称罗素为 “美国天文学家的院长”。 多年来，罗素无疑被视为该领域的领导者，来自世界各地的同事就许多天文学问题征求了罗素的意见。 如今，天文学家可以获得的最高荣誉之一是美国天文学会颁发的名为罗素奖的奖项，该奖项是为纪念他而设立的。

H—R 图的特点

跟随Hertzsprung和Russell，让我们根据附近一组选定的恒星的亮度绘制其温度（或光谱等级），看看我们发现了什么（图\(\PageIndex{3}\)）。 这样的图通常被称为 Hertzsprung—Russell 图，缩写为 H—R 图。 它是天文学中最重要和最广泛使用的图表之一，其应用范围远远超出了一个多世纪前最初开发的目的。

图\(\PageIndex{3}\) H—R 精选恒星样本图。 在这样的图中，亮度是沿垂直轴绘制的。 沿着水平轴，我们可以绘制温度或光谱类型（有时也称为光谱类别）。 几颗最亮的恒星都是用名字识别的。 大多数恒星落在主序列上。

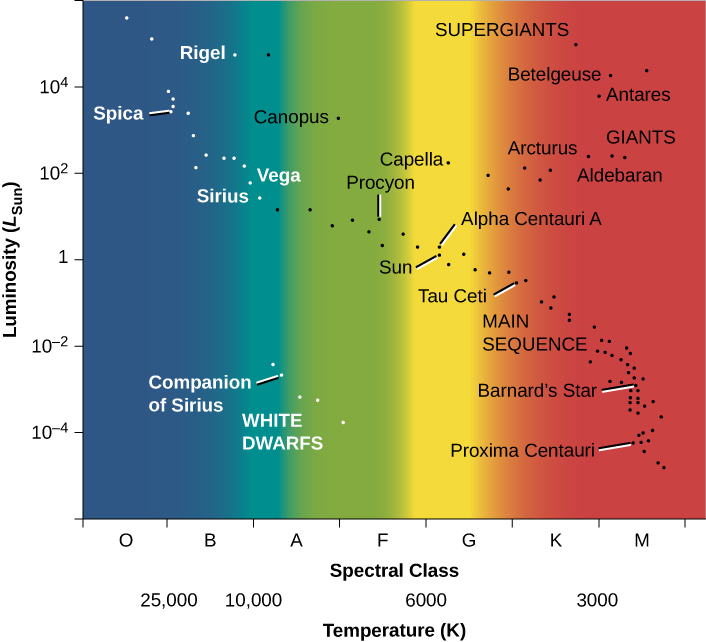
通常绘制 H—R 图的方式是，温度向左升高，亮度向上升高。 请注意，这与我们的身高和体重图（图\(\PageIndex{1}\)）相似。 像人一样，恒星不是随机分布在图表上的，就像它们表现出亮度和温度的所有组合时那样。 相反，我们看到恒星聚集在 H—R 图的某些部分。 绝大多数是沿着从左上角（热、高亮度）到右下角（冷、亮度较低）的狭窄顺序排列的。 这个点波段被称为主序列。 它代表了温度和亮度之间的关系，大多数恒星都遵循这种关系。 我们可以总结这种关系，说较热的恒星比较冷的恒星更明亮。

但是，许多恒星位于 H—R 图的主序列上方，位于右上角区域，那里的恒星温度低，亮度高。 一颗恒星怎么能立刻变酷，这意味着恒星上的每一平方米都不会消耗那么多的能量，但是非常发光？ 唯一的办法是让恒星变得巨大 —— 其表面有如此多的平方米，以至于总能量输出仍然很大。 这些恒星一定是巨星或超级巨星，我们之前讨论过的直径很大的恒星。

图的左下角还有一些恒星，它们温度高，亮度低。 如果它们的表面温度很高，那颗恒星上的每平方米都会消耗大量能量。 那整颗星怎么会变暗呢？ 一定是它的总表面积很小；这样的恒星被称为白矮星（白色是因为在这样的高温下，它们发出的电磁辐射的颜色混合在一起，使它们看起来像蓝白色）。 稍后我们将更多地介绍这些令人费解的物体。 图为大量恒星样本的 H—R 示意图，绘制的目的是使不同类型的恒星更加明显。

图\(\PageIndex{4}\)示多颗恒星的H—R示意图. 在这样的图表中，百分之九十的恒星落在称为主序列的窄带上。 少数恒星位于右上角；它们既凉爽（因此也是红色）又明亮，一定是巨星。 有些恒星落在图的左下角；它们既热又暗，一定是白矮星。

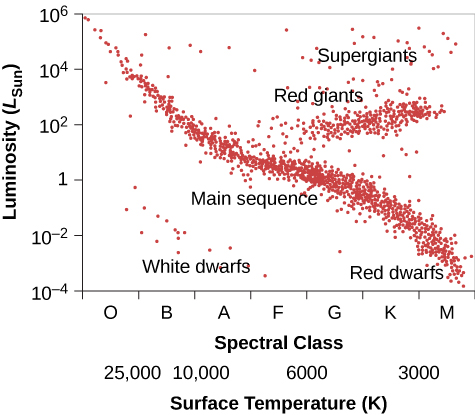
现在，回想一下我们对星空调查的讨论。 很难绘制出能真正代表所有恒星的 H—R 图，因为大多数恒星都非常微弱，以至于我们看不见邻近区域之外的恒星。 之所以选择图中绘制的星星\(\PageIndex{3}\)，是因为它们的距离是已知的。 该样本省略了许多本质上微弱的恒星，这些恒星位于附近，但尚未测量其距离，因此它显示的微弱主序列恒星比 “公平” 的图表要少。 为了真正代表恒星群体，应该为一定距离内的所有恒星绘制一张 H—R 图。 不幸的是，只有距离太阳 10 到 20 光年的恒星，我们的知识才相当完整，其中没有巨星或超级巨星。 尽管如此，根据许多调查（现在用新的、更强大的望远镜可以做更多的事情），我们估计，在我们的太空中，总共约有90％的真正恒星（不包括褐矮星）是主序列恒星，大约10％是白矮星，不到1％是巨星或超级巨星。

这些估计值可以直接用于了解恒星的寿命。 请允许我们再简单地与人进行类比。 假设我们调查人就像天文学家调查恒星一样，但我们希望将注意力集中在6至18岁年轻人的位置上。 调查小组在24小时内随时随地搜集有关这些青少年的发现地点的数据。 有些是在当地的披萨店里找到的，有些在家里睡着了，有些在看电影，还有很多在学校。 在调查了大量年轻人之后，这些小组确定的一件事是，在24小时内，平均而言，所有年轻人中有三分之一在学校。

他们如何解释这个结果？ 这是否意味着三分之二的学生逃学，其余三分之一的学生将所有时间都花在学校上？ 不，我们必须记住，调查小组在整整24小时内都对年轻人进行了统计。 一些调查小组在晚上工作，那时大多数年轻人都在家里睡觉，而另一些则在下午晚些时候工作，那时大多数年轻人正在放学回家的路上（更有可能享受披萨）。 但是，如果调查确实具有代表性，我们可以得出结论，如果平均有三分之一的年轻人上学，那么6至18岁的人必须将大约三分之一的时间花在学校上。

我们可以为星星做类似的事情。 我们发现，平均而言，90% 的恒星位于 H—R 图的主序列上。 如果我们能用主序列来识别某个活动或生命阶段，那么恒星必须在该活动或生命阶段度过90％的生命。

了解主序列

在《太阳：核强国》中，我们讨论了太阳作为代表性恒星的问题。 我们看到，像太阳这样的恒星 “谋生” 的是通过核聚变过程将质子转化为内部深处的氦气，从而产生能量。 质子聚变为氦气是恒星极好的、持久的能量来源，因为每颗恒星的大部分由氢原子组成，而氢原子的原子核是质子。

我们对恒星如何随时间演变的计算机模型向我们表明，一颗典型的恒星将花费大约90％的生命将其核心中丰富的氢气融合成氦气。 这就很好地解释了为什么在 H—R 图的主序列中发现了 90% 的恒星。 但是，如果主序列上的所有恒星都在做同样的事情（融合氢气），为什么它们会沿着一系列点分布呢？ 也就是说，为什么它们的亮度和表面温度不同（这是我们在H—R图上绘制的）？

为了帮助我们了解主序列恒星有何不同，我们可以使用我们对模型恒星的研究中最重要的结果之一。 天体物理学家已经能够证明，处于平衡状态并从核聚变中获得所有能量的恒星的结构完全由两个量唯一决定：恒星的总质量和组成。 这个事实解释了 H—R 图的许多特征。

想象一下，一群由星际 “原材料” 云形成的恒星团，其化学成分与太阳相似。（我们将在《恒星的诞生》和《太阳系外行星的发现》中更详细地描述这个过程，但就目前而言，细节不关心我们。） 在这样的云中，所有变成恒星的气体和尘埃团都以相同的化学成分开始，彼此之间仅在质量上有所不同。 现在假设我们计算出每颗恒星的模型，其时间是它变得稳定并从核反应中获得能量，但在这些反应没有时间明显改变其成分之前。

为这些恒星计算的模型使我们能够确定它们的亮度、温度和大小。 如果我们在 H—R 图上绘制模型的结果（每颗模型恒星对应一个点），我们得到的结果看起来就像我们看到的真实恒星的主序列。

这是我们这样做时所发现的。 质量最大的模型星是最热、最亮的恒星，它们位于图的左上角。

质量最小的模型恒星是最酷、发光度最低的，它们位于图表的右下角。 其他模型星星都位于一条沿对角线穿过图表的直线上。 换句话说，主序列原来是一系列恒星质量。

如果你考虑一下，这是有道理的。 质量最大的恒星具有最大的重力，因此可以最大程度地压缩它们的中心。 这意味着它们是内部最热的，最擅长从内心深处的核反应中产生能量。 因此，它们的发光亮度最高，表面温度最高。 反过来，质量最低的恒星是内部最酷的恒星，在产生能量方面效果最差。 因此，它们的发光度最低，最终成为表面上最酷的。 我们的太阳位于这些极端的中间位置（如图所示\(\PageIndex{3}\)）。 表中列出了代表性的主序列恒星（不包括褐矮星，它们不是真正的恒星）的特征\(\PageIndex{2}\)。

表\(\PageIndex{2}\)：主序列恒星的特征

光谱类型	弥撒（太阳 = 1）	亮度（太阳 = 1）	温度	半径（太阳 = 1）
O5	40	7×10 ^5	40,000 K	18
B0	16	2.7×10 ^5	28,000 K	7
A0	3.3	55	10,000 K	2.5
F0	1.7	5	7500 K	1.4
G0	1.1	1.4	6000 K	1.1
K0	0.8	0.35	5000 K	0.8
M0	0.4	0.05	3500 K	0.6

请注意，我们之前已经看到了90％的数字。 这正是我们之前在研究质量-亮度关系时发现的（图见\(18.2.6\)第 18.2 节）。 我们观察到90％的恒星似乎遵循这种关系；在我们的H—R图中，这些是位于主序列上的所有恒星中的90％。 我们的模型和观察结果一致。

那么 H—R 图上的其他恒星 —— 巨星和超级巨星，还有白矮星？ 正如我们将在接下来的几章中看到的那样，这些是主序列恒星随着年龄的增长而变成的东西：它们是恒星生命的后期阶段。 当恒星消耗其核燃料时，其能量来源会发生变化，其化学成分和内部结构也会发生变化。 这些变化会导致恒星改变其亮度和表面温度，因此它不再位于我们图中的主序列上。 因为恒星在生命的后期阶段花费的时间要少得多，所以我们在H—R图的这些区域看到的恒星减少了。

恒星亮度、直径和密度的极端值

我们可以使用 H—R 图来探索恒星中大小、亮度和密度的极端情况。 这些极限的明星不仅对《吉尼斯世界纪录大全》的粉丝很有趣；它们可以教会我们很多关于星星如何运作的知识。 例如，我们看到最大的主序列恒星是发光度最高的恒星。 我们知道有几颗极端恒星的亮度比太阳高一百万倍，其质量超过太阳质量的100倍。 这些超发光的恒星位于 H—R 图的左上角，它们是光谱类型为 O 的极热、非常蓝色的恒星。这些恒星在太空中很远的距离最引人注目。

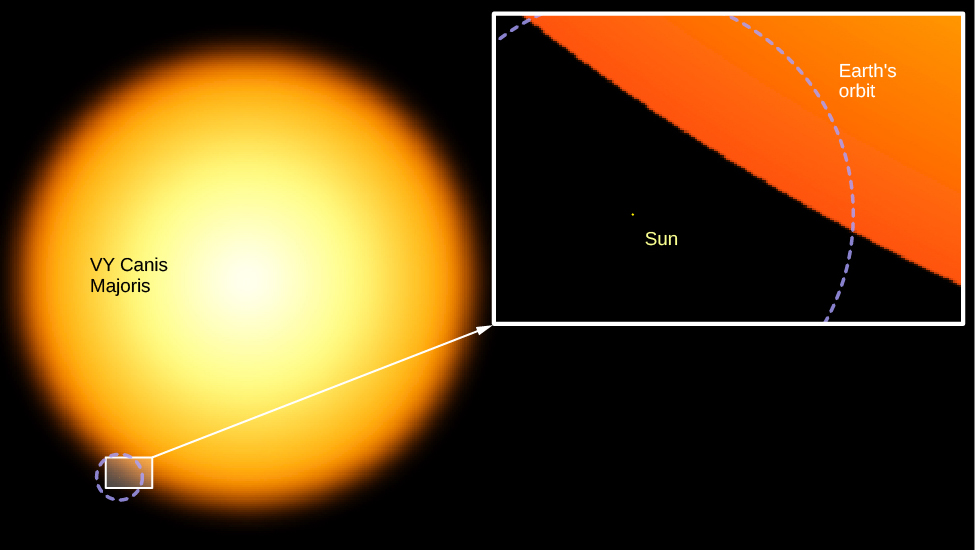
H—R 图上角的酷炫超级巨星的亮度是太阳的 10,000 倍。 此外，这些恒星的直径比太阳的直径大得多。 如上所述，一些超级巨星非常大，以至于如果太阳系能够以一个超级巨星为中心，则恒星的表面将位于火星轨道之外（见图\(\PageIndex{5}\)）。 在接下来的章节中，我们将不得不问，什么过程可以使恒星膨胀到如此巨大的大小，以及这些 “肿胀” 的恒星在膨胀状态下能持续多久。

图\(\PageIndex{5}\)《太阳与超级巨人》。 在这里，你可以看到与已知最大的恒星之一：超级巨星 VY Canis Majoris 相比，太阳看起来有多小。

相比之下，位于主序列下端的非常常见的红色、凉爽、低亮度的恒星比太阳小得多，也更紧凑。 这种红矮星的一个例子是罗斯614B，它的表面温度为2700 K，亮度仅为太阳的1/2000。 我们称这样的恒星为矮星，因为它的直径只有太阳的1/10。 亮度如此低的恒星的质量也很低（大约是太阳的1/12）。 这种质量和直径的组合意味着它被压缩得如此之大，以至于恒星的平均密度约为太阳的80倍。 实际上，它的密度必须高于在地球表面发现的任何已知固体的密度。 （尽管如此，恒星始终是由气体组成的，因为它的中心太热了。）

但是，微弱的红色主序列恒星并不是密度最高的恒星。 位于 H—R 图左下角的白矮星的密度要高很多倍。

白矮星

1862 年发现了第一颗白矮星。 它被称为 Sirius B，它与天空中最亮的恒星 Sirius A 形成了一个二进制系统。 它长时间没有被发现和分析，因为在附近的 Sirius A 的眩光下，它的微弱光线往往会消失（图\(\PageIndex{6}\)）。 （由于小天狼星通常被称为狗星——它是大狗 Canis Major 星座中最亮的恒星，因此 Sirius B 有时被昵称为 Pup。）

图\(\PageIndex{6}\)二天狼星及其白矮星同伴的视图。 (a) 用哈勃太空望远镜拍摄的（可见光）图像显示了明亮的 Sirius A，其下方和左侧是微弱的 Sirius B。（b）这张小天狼星系统的照片是用钱德拉 X 射线望远镜拍摄的。 现在，明亮的物体是白矮星同伴，Sirius B. Sirius A 是它上方的微弱物体；我们从小天狼星那里看到的实际上可能不是 X 射线辐射，而是泄漏到探测器中的紫外线。 请注意，这两个物体的紫外线强度与可见光下的紫外线强度完全相反，因为天狼星B更热，发出的辐射频率更高。

我们现在已经找到了成千上万的白矮星。 该表\(\PageIndex{1}\)显示，我们当地邻域的真星（光谱类型为O—M）中约有7％是白矮星。 典型白矮星的一个很好的例子是附近的恒星 40 Eridani B。它的表面温度相对较高 12,000 K，但其亮度仅为 1/275 L 太阳。 计算表明，它的半径仅为太阳的1.4％，或与地球的半径大致相同，其体积为太阳的2.5×10—6。 但是，它的质量是太阳质量的0.43倍，略低于一半。 要将如此巨大的质量装入如此微小的体积中，恒星的密度必须是太阳密度的17万倍左右，或超过200,000 g/cm ³。 一茶匙这种材料的质量大约为50吨！ 在如此巨大的密度下，物质不可能以其通常的状态存在；我们将在《星之死》中研究这种物质的特殊行为。 现在，我们只注意到白矮星是垂死的恒星，他们富有成效的生命即将结束，为故事的结束做好了准备。

英国天体物理学家（兼科学普及者）亚瑟·爱丁顿（1882-1944）用这种方式描述了第一个已知的白矮星：

小天狼星的同伴在解码后传达的信息是：“我的材料密度比你见过的任何东西都要密度三千倍。 你可以把我的一大堆材料放进火柴盒里。” 人们能对这样的事情做出什么回应？ 好吧，我们大多数人在1914年的回答是：“闭嘴；别胡说八道。”

但是，如今，天文学家不仅接受存在像白矮星一样密集的恒星，而且（正如我们将看到的）在寻求了解不同类型恒星演变的过程中发现了更密集和更奇怪的天体。

关键概念和摘要

Hertzsprung—Russell 图或 H—R 图是恒星亮度与表面温度的关系图。 大多数恒星位于主序列上，主序列沿对角线延伸到H—R图，从高温和高亮度到低温和低亮度。 恒星在主序列上的位置由其质量决定。 高质量恒星比主序列上的低质量恒星发射更多的能量并且更热。 主序列恒星的能量来自质子聚变为氦气。 大约 90% 的恒星位于主序列上。 只有大约 10% 的恒星是白矮星，只有不到 1% 的恒星是巨星或超级巨星。

词汇表

H—R 图

（Hertzsprung—Russell 图）一组恒星的亮度与表面温度（或光谱类型）的对比图

主序列

Hertzsprung—Russell 图上的一系列恒星，包含大部分恒星，从左上角向右下角延伸

白矮星

一颗低质量恒星，它已经耗尽了大部分或全部核燃料并已崩溃到非常小的体积；这样的恒星已接近其最终生命状态