18.3: 恒星的直径
- Page ID
- 202060
学习目标
在本节结束时,您将能够:
- 描述用于确定恒星直径的方法
- 识别黯然失色的双星光曲线中与各个组件的直径相对应的部分
测量太阳的直径很容易。 它的角直径(即它在天空中的表观大小)约为 1/2°。 如果我们知道太阳在天空中所占的角度以及它有多远,我们就可以计算出它的真实(线性)直径,即139万千米,大约是地球直径的109倍。
不幸的是,太阳是唯一一颗易于测量角直径的恒星。 所有其他恒星都很远,即使是最大的地面望远镜,它们看起来也像是精确的光点。 (它们通常看起来更大,但这仅仅是地球大气层湍流造成的失真。) 幸运的是,天文学家可以使用几种技术来估计恒星的大小。
被月亮挡住的星星
一种可以提供非常精确的直径但只能用于几颗恒星的技术是观察月亮在恒星面前经过时光的变暗情况。 天文学家(非常精确地)测量的是,当月球边缘穿过恒星的圆盘时,恒星的亮度降至零所需的时间。 由于我们知道月球在绕地球的轨道上移动的速度有多快,因此可以计算出恒星的角直径。 如果还知道与恒星的距离,我们可以以千米为单位计算其直径。 这种方法仅适用于恰好位于十二生肖沿线的相当明亮的恒星,从地球上看,月亮(或者更罕见的是行星)可以在它们面前经过。
使双星黯然失色
大量恒星的精确大小来自对黯然失色的双星系统的测量,因此我们必须从主要故事中绕道来研究这种类型的恒星系统。 有些双星的排列方式是,从地球上观察时,每颗恒星在每次旋转时都会在另一颗恒星面前经过(图\(\PageIndex{1}\))。 当一颗恒星阻挡另一颗恒星的光,阻止它到达地球时,系统的亮度就会降低,天文学家说日食已经发生。
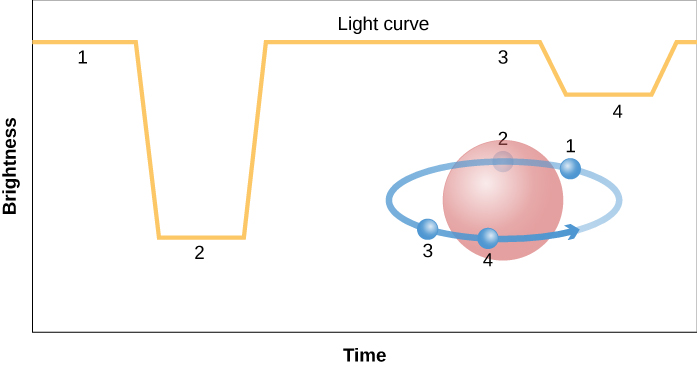
第一个黯然失色的二进制文件的发现帮助解决了天文学中一个长期存在的难题。 英仙座星座中的阿尔戈尔恒星以一种奇怪但规律的方式改变其亮度。 通常,Algol 是一颗相当明亮的恒星,但是每隔 2 天 20 小时 49 分钟,它会逐渐消失到常规亮度的三分之一。 几个小时后,它又变亮到正常状态。 如果你知道要寻找什么,即使没有望远镜,这种效果也很容易看出来。
1783 年,一位名叫约翰·古德里克(1764—1786 年)的年轻英国天文学家对阿尔戈尔进行了仔细研究(有关约翰·古德里克生活和工作的讨论,请参阅第 19.3 节中约翰·古德里克的专题报道)。 尽管古德里克既听不见也不会说话,但在他短暂生命的21年中,他发现了许多重大发现。 他认为,Algol 不寻常的亮度变化可能是由于一个看不见的同伴经常在更亮的恒星面前经过并阻挡其光线。 不幸的是,古德里克无法检验这个想法,因为直到大约一个世纪后,设备才变得足够好,可以测量Algol的频谱。
1889年,德国天文学家赫尔曼·沃格尔(Hermann Vogel)(1841-1907)证明,与米扎尔一样,Algol是一种光谱二进制文件。 没有观察到 Algol 的光谱线是双倍的,因为与较亮的恒星相比,两颗微弱的恒星发出的光太少,因此其线条在复合光谱中不显眼。 尽管如此,这颗较亮的恒星的线条周期性地来回移动,这证明它围绕着一个看不见的同伴旋转。 (要将恒星识别为光谱二进制文件,两个分量的线条都不必可见。)
Algol 是光谱二进制文件的发现证实了古德里克的假设。 星星旋转的飞机几乎沿边缘方向转向我们的视线,每一次旋转中,每颗恒星都会在另一颗恒星面前经过。 (Algol 系统中微弱恒星的日食不太明显,因为其中被覆盖的部分对系统的总光影响不大。 但是,可以通过仔细测量来检测到第二次日食。)
如果从正确的方向观察,任何双星都会在其轨道平面附近产生日食,因此一颗恒星在另一颗恒星的前面经过(见图\(\PageIndex{1}\))。 但是从我们在地球的角度来看,只有少数双星系统是以这种方式定向的。
天文学和神话:恶魔之星 ALGOL 和英雄英仙座
Algol 这个名字来自阿拉伯语 Ras al Ghul,意思是 “恶魔的头”。 1 英语中的 “食尸鬼” 一词具有相同的派生词。 正如《观测天空:天文学的诞生》中所讨论的那样,许多明亮的恒星都有阿拉伯名字,因为在中世纪欧洲漫长的黑暗时代,正是阿拉伯天文学家保存和扩展了希腊和罗马对天空的了解。 对恶魔的提法是古希腊英雄英仙座传说的一部分,英雄英仙座以我们在其中找到阿尔戈尔的星座来纪念他,他的冒险涉及许多与北方星座相关的角色。
英仙座是宙斯(罗马版本中的木星)所生的众多半神英雄之一,宙斯是希腊神话中的众多众神之王。 简而言之,宙斯有一只巡回的眼睛,总是在和一个喜欢他的人类少女一起生一个人或其他人。 (英仙座源自 P er Zeus,意思是 “宙斯之父”。) 英仙座被一个(可以理解的)心烦意乱的继父与母亲漂流,在爱琴海的一个小岛上长大。 那里的国王对英仙座的母亲产生了兴趣,试图通过给他分配一项极其艰巨的任务来摆脱他。
在最引以为豪的时刻,一位名叫美杜莎的漂亮年轻女子将自己的金发与雅典娜女神(罗马人的密涅瓦)的金发进行了比较。 希腊众神对被比作凡人并不友善,雅典娜把美杜莎变成了戈尔贡:一个可怕的、邪恶的生物,用扭动的蛇换头发,一张脸把任何看着它的人都变成了石头。 英仙座被赋予了杀死这个恶魔的任务,这似乎是让他永远摆脱困境的肯定方法。
但是因为英仙座有神作为父亲,所以其他一些神灵给了他完成这项工作的工具,包括雅典娜的反光盾牌和爱马仕的有翼凉鞋(罗马故事中的水星)。 通过飞越她,只看她的倒影,英仙座能够在不直视美杜莎的情况下砍掉她的头。 英仙座带着她的头(很方便地,即使不附着她的身体,旁观者仍然可以变成石头),继续进行其他冒险。
接下来他来到了一个多岩石的海边,那里的吹嘘使另一个家庭陷入了与众神的严重麻烦。 仙后座女王敢将自己的美丽与海神波塞冬(罗马神话中的海王星)的女儿Nereids的美丽相提并论。 波塞冬非常生气,以至于他创造了一个名为Cetus的海怪来摧毁王国。 仙后座陷入困境的丈夫 Cepheus 国王咨询了神谕,神谕告诉他必须把漂亮的女儿仙女座献给怪物。
当英仙座过来发现仙女座被拴在海边的一块岩石上等待她的命运时,他把怪物变成石头救了她。 (神话学者实际上将这个故事的本质追溯到古代美索不达米亚的古老传说,神灵英雄马尔杜克战胜了一个名为蒂亚玛特的怪物。 具有象征意义的是,像英仙座或马尔杜克这样的英雄通常与太阳、拥有夜晚力量的怪物以及拥有脆弱黎明之美的美丽少女联系在一起,太阳在夜间与黑暗斗争后会释放出来。)
这些希腊传说中的许多角色可以看作是天空中的星座,不一定与他们的同名人物相似,但可以提醒人们故事。 例如,徒劳的仙后座每年冬天都被判处非常靠近天极,永久绕天旋转,倒挂在天上。 古人想象仙女座仍然被拴在她的岩石上(看见星链比认出这个星群中的漂亮少女要容易得多)。 英仙座在她旁边,美杜莎的头从腰带上摆动。 Algol 代表着这个 gorgon Head,在这样的故事中长期以来一直与邪恶和坏运联系在一起。 一些评论家推测,恒星亮度的变化(可以用肉眼观察)可能导致了它令人不快的声誉,古人认为这种变化是一种邪恶的 “眨眼”。
黯然失色的双星的直径
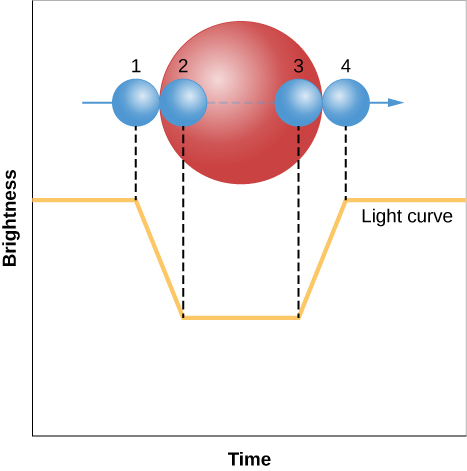
现在,我们回到故事的主线,讨论如何使用所有这些来测量恒星的大小。 该技术涉及绘制一个黯然失色的二进制的光曲线,该图形绘制亮度如何随时间变化。 让我们考虑一个假设的二进制系统,其中恒星的大小差异很大,如图所示\(\PageIndex{2}\)。 为了让生活变得轻松,我们将假设轨道完全是边缘观察。
尽管我们无法在这样的系统中分别看到两颗恒星,但光曲线可以告诉我们发生了什么。 当较小的恒星刚开始穿过较大的恒星(我们称之为初次接触点)后面时,亮度开始下降。 在称为第二次接触的地方,日食变为全食(较小的恒星被完全隐藏)。 在全食(第三次接触)结束时,较小的恒星开始出现。 当较小的恒星到达最后一次接触时,日食就完全结束了。
要了解这如何允许我们测量直径,请仔细看图\(\PageIndex{2}\)。 在第一次和第二次接触之间的时间间隔内,较小的恒星移动的距离等于其自身直径。 在从第一次接触到第三次接触的时间间隔内,较小的恒星移动的距离等于较大恒星的直径。 如果两颗恒星的光谱线在二进制光谱中都可见,则可以通过多普勒偏移来测量较小恒星相对于较大恒星的速度。 但是,知道较小的恒星的移动速度以及覆盖一段距离需要多长时间可以分辨出该距离的跨度,在本例中是恒星的直径。 速度乘以从第一次接触到第二次接触的时间间隔得出较小恒星的直径。 我们将速度乘以第一次和第三次接触之间的时间,得出较大恒星的直径。
实际上,使二进制文件黯然失色的情况通常要复杂一些:轨道通常无法完全处于边缘状态,每颗恒星发出的光可能只能被另一颗恒星部分阻挡。 此外,双星轨道就像行星的轨道一样,是椭圆,而不是圆形。 但是,所有这些效果都可以通过对光线曲线的非常仔细的测量来分辨出来。
使用辐射定律得出直径
另一种测量恒星直径的方法是利用斯特凡-玻尔兹曼定律来确定辐射能量与温度之间的关系(参见辐射和光谱)。 在这种方法中,能量通量(黑体,如太阳)每平方米每秒发射的能量)由下式给出
\[F= \sigma T^4 \nonumber\]
其中\(\sigma\)是常数,\(T\)是温度。 球体(如恒星)的表面积由下式给出
\[A=4 \pi R^2 \nonumber\]
然后,恒星的亮度 (\(L\)) 由其表面积(以平方米为单位)乘以能量通量得出:
\[L=(A \times F)\]
以前,我们确定了 Sirius 二进制系统中两颗恒星的质量。 尽管两颗恒星的温度几乎相同,但天狼星发出的能量是其微弱的同伴恒星的8200倍。 亮度的极大差异是由于半径的差异,因为两颗恒星的温度和能量通量几乎相同。 为了确定两颗恒星的相对大小,我们采用相应亮度的比例:
\[\begin{array}{c} \frac{L_{\text{Sirius}}}{L_{\text{companion}}}=\frac{ \left( A_{\text{Sirius}} \times F_{\text{Sirius}} \right)}{ \left( A_{\text{companion}} \times F_{\text{companion}} \right)} \\ = \frac{A_{\text{Sirius}}}{A_{\text{companion}}}= \frac{4 \pi R^2_{\text{Sirius}}}{4 \pi R^2_{\text{companion}}}= \frac{R^2_{\text{Sirius}}}{R^2_{\text{companion}}} \\ \frac{L_{\text{Sirius}}}{L_{\text{companion}}}=8200= \frac{R^2_{\text{Sirius}}}{R^2_{\text{companion}}} \end{array} \nonumber\]
因此,通过取相对亮度的平方根可以得出两颗恒星的相对大小。 因为\(\sqrt{8200} = 91\),小天狼星的半径比其微弱同伴的镭大91倍。
此处显示的确定半径的方法要求两颗星都可见,但情况并非总是如此。
恒星直径
多年来,许多恒星大小测量的结果表明,附近的大多数恒星大致相当于太阳的大小,典型直径为一百万千米左右。 正如我们所预料的那样,微弱的恒星通常比发光度更高的恒星小。 但是,这种简单的概括有一些明显的例外。
事实证明,一些非常明亮的恒星,那些也是红色的(表示相对较低的表面温度)的恒星,确实是巨大的。 这些恒星被恰当地称为巨星或超级巨星。 例如 Betelgeuse,它是猎户座星座中第二亮的恒星,也是我们天空中最亮的十几颗恒星之一。 值得注意的是,它的直径大于 10 AU(15 亿千米!) ,足够大,足以填满几乎和木星一样远的整个内部太阳系。 在《从青春期到晚年的恒星》中,我们将详细探讨导致此类巨星和超级巨星形成的进化过程。
观看这段恒星大小比较视频,获得引人注目的视觉效果,突出显示恒星与行星的大小以及恒星之间的大小范围。
摘要
恒星的直径可以通过测量物体(月球、行星或同伴恒星)经过其前方并阻挡其光线所花费的时间来确定。 黯然失色的二进制系统(恒星在彼此面前穿过)的成员的直径可以通过分析它们的轨道运动来确定。
脚注
3 蝙蝠侠漫画书和电影的粉丝会意识到这个名字是该系列中一个大反派使用的。
词汇表
- 超过二进制文件
- 一颗双星,其中两颗恒星的旋转平面几乎位于我们的视线边缘,因此一颗恒星的光线会因另一颗恒星在其前方经过而周期性地减弱


