18.2: 测量恒星质量

学习目标

在本节结束时，您将能够：

• 区分不同类型的双星系统
• 了解我们如何运用牛顿版本的开普勒第三定律来推导出双星系统中恒星质量的总和
• 应用恒星质量和恒星亮度之间的关系来确定恒星的物理特征

恒星的质量——它所含的物质量——是它最重要的特征之一。 如果我们知道一颗恒星的质量，正如我们将看到的那样，我们可以估计它会发光多长时间以及它的最终命运如何。 然而，恒星的质量很难直接测量。 不知何故，我们需要将一颗恒星放置在相当于宇宙尺度的宇宙上。

幸运的是，并非所有恒星都像太阳一样生活，与其他恒星隔绝。 大约一半的恒星是双星——两颗相互绕轨道运行的恒星，由重力结合在一起。 双星的质量可以通过测量其轨道来计算，就像通过测量太阳周围行星的轨道可以得出太阳的质量一样（参见 Orbits and Gravity）。

二进制星

在我们更详细地讨论如何测量质量之前，我们将仔细研究成对出现的恒星。 第一颗双星是在1650年发现的，距离伽利略开始用望远镜观测天空不到半个世纪。 意大利天文学家约翰·巴蒂斯特·里乔利（1598—1671 年）指出，位于北斗七星手柄中间的米扎尔星以两颗星的形式通过他的望远镜出现。 自那次发现以来，已经对成千上万的双星进行了编目。 （天文学家称天空中任何一对看起来彼此靠近的恒星都是双星，但并非所有这些恒星都构成真正的二进制恒星，也就是说，并非所有恒星在物理上都有关联。 有些只是恒星的偶然对齐方式，实际上与我们的距离不同。） 尽管恒星通常成对出现，但也有三重和四重系统。

一颗著名的双星是位于双子星座中的Castor。 到1804年，天文学家威廉·赫歇尔（William Herschel）也发现了天王星，他注意到蓖麻的微弱成分相对于较亮成分的位置略有变化。 （我们使用 “组件” 一词来表示恒星系统的成员。） 这里有证据表明，一颗恒星正在绕另一颗恒星移动。 这实际上是太阳系之外存在引力影响的第一个证据。 双星的轨道运动如图所示\(\PageIndex{1}\)。 用望远镜可以看到两颗恒星的双星系统被称为视觉二进制星系统。

双星的数字\(\PageIndex{1}\)革命。 该图显示了对两颗恒星相互旋转的七次观测结果，一颗是褐矮星，另一颗是超酷的 L 矮星。 轨道上的每个红点（由蓝色椭圆显示）对应于其中一个矮星相对于另一个矮星的位置。 这对恒星在不同的日期看起来不同的原因是，有些图像是用哈勃太空望远镜拍摄的，而另一些则是从地面拍摄的。 箭头指向与每个红点的位置相对应的实际观测值。 根据这些观测结果，一个国际天文学家小组首次直接测量了一颗超酷的褐矮星的质量。 这颗矮星的大小几乎不及木星的大小，其重量仅为我们太阳质量的8.5％。

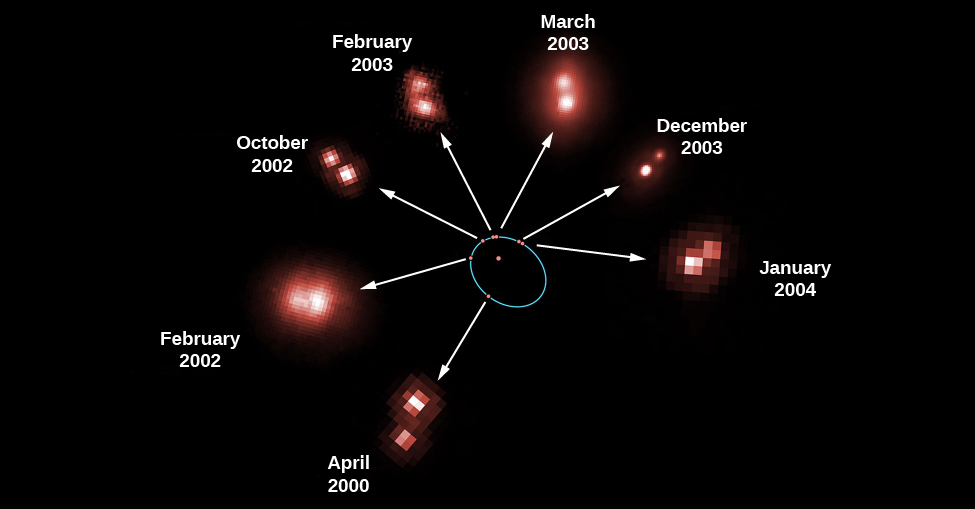
1889 年，哈佛大学的爱德华·皮克林（1846—1919 年）发现了第二类双星，实际上只能直接看到其中一颗恒星。 他正在研究米扎尔的光谱，发现较亮的恒星光谱中的暗吸收线通常是两倍。 不仅有两条线，天文学家通常只能看到一条线，而且两条线的间距也在不断变化。 有时，这些台词甚至变得单曲。 皮克林正确地推断出，米扎尔中较亮的部分叫做 Mizar A，其本身实际上是两颗在 104 天内相互旋转的恒星。 像 Mizar A 这样的恒星被称为光谱二进制星，它在通过望远镜拍摄或目视观测时显示为单星，但光谱学显示其实是双星。

顺便说一句，米扎尔就是一个很好的例子，说明了这样的恒星系统有多复杂。 几个世纪以来，众所周知，米扎尔有一个叫阿尔科的微弱同伴，没有望远镜就能看见。 Mizar 和 Alcor 形成了光学双星 —— 一对恒星在天空中近距离出现，但不会相互绕轨道运行。 正如 Riccioli 在 1650 年发现的那样，通过望远镜可以看出 Mizar 还有另一个更近的同伴在绕它运行；因此，米扎尔是一个视觉二进制文件。 构成这个视觉二进制文件的两个组件，分别是 Mizar A 和 Mizar B，都是光谱二进制文件。 所以，米扎尔实际上是一个由四重恒星组成的系统。

严格来说，用说一颗恒星绕另一颗恒星运行来描述双星系统的运动是不正确的。 重力是一种相互的吸引力。 每颗恒星对另一颗恒星施加引力，结果两颗恒星绕它们之间的一个称为质心的点运行。 想象一下，两颗星星坐在跷跷板的两端。 为了使跷跷板保持平衡，支点必须位于质心，而且它总是更接近质量更大的恒星（图\(\PageIndex{2}\)）。

图\(\PageIndex{2}\) Binary Star 系统。 在双星系统中，两颗恒星都绕其质心运行。 该图显示了两颗质量不同的恒星与其质心的相对位置，类似于两个质量必须位于跷跷板上才能保持水平的方式。 质量较高的恒星将在离质心更近的地方被发现，而质量较低的恒星将离质心更远。

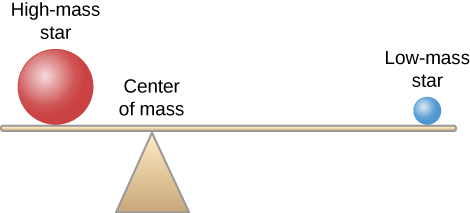
该图\(\PageIndex{3}\)显示了两颗恒星（A和B）绕其质心移动，以及我们在不同时间从系统观测到的每颗恒星光谱中的一条线。 当一颗恒星相对于质心接近我们时，另一颗恒星正在从我们身边消失。 在左上角的插图中，恒星A正在向我们移动，因此其光谱中的线向光谱的蓝端多普勒移动。 星星B正在远离我们，所以它的线条显示了红移。 当我们观察两颗恒星的复合光谱时，这条线看起来是双倍的。 当两颗恒星都穿过我们的视线（既不远离也不向我们）移动时，它们的径向速度（两颗恒星质心的径向速度）相同；因此，两颗恒星的光谱线汇聚在一起。 如图中底部的两个插图所示\(\PageIndex{3}\)。

图形两颗恒星相互旋转的\(\PageIndex{3}\)运动以及光谱显示的内容。 我们看到速度的变化，因为当一颗恒星向地球移动时，另一颗恒星正在移动；半个周期后，情况发生了逆转。 多普勒偏移会导致光谱线来回移动。 在图表1和图3中，可以看到来自两颗星的线条彼此分开得很好。 当两颗恒星垂直于我们的视线移动时（也就是说，它们既没有朝向我们移动，也没有远离我们），这两条线是完全叠加的，因此在图 2 和图 4 中，我们只能看到一条光谱线。 请注意，在图表中，恒星对的轨道相对于观众稍微倾斜（或者如果观众在天空中观看，则轨道将相对于观众的视线倾斜）。 如果轨道正好在页面或屏幕（或天空）的平面上，那么它看起来几乎是圆形的，但我们看不到径向速度的变化（运动的任何部分都不会朝向我们或远离我们）。 如果轨道垂直于页面或屏幕的平面，那么星星似乎会沿直线来回移动，我们将看到尽可能大的径向速度变化。

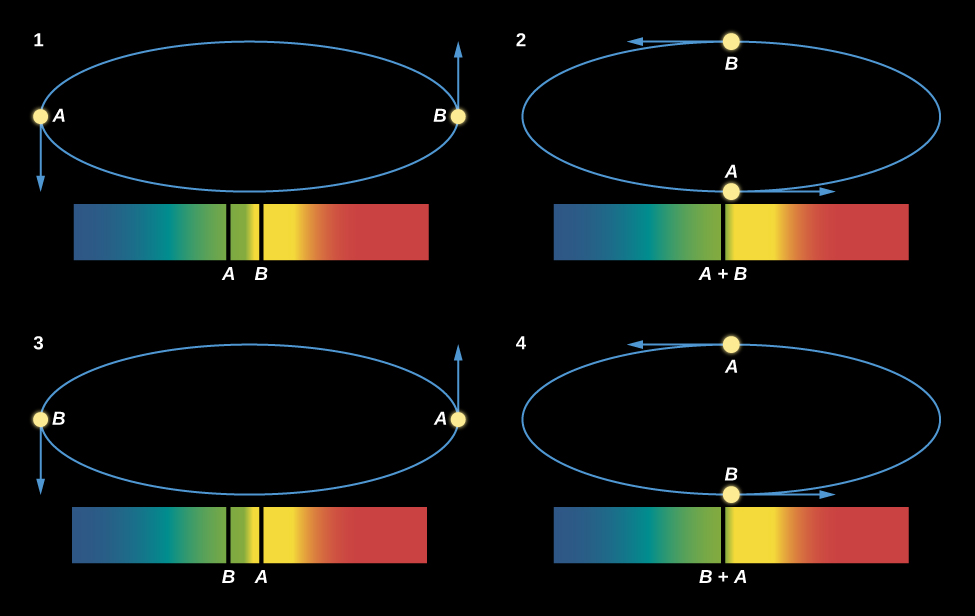
显示恒星速度如何随时间变化的图称为径向速度曲线；图中二进制系统的曲线如图\(\PageIndex{3}\)所示\(\PageIndex{4}\)。

图：光谱二进制系统中的\(\PageIndex{4}\)径向速度。 这些曲线描绘了光谱二进制系统中两颗恒星的径向速度，显示了恒星如何交替接近地球并从地球消退。 请注意，正速度意味着恒星正在远离我们，负速度意味着恒星正在向我们移动。 系统本身的质心也在远离我们，以每秒 40 千米的正速度表示。 曲线上与图中插图相对应的位置用图编号 (1—4) 标记。\(\PageIndex{3}\)

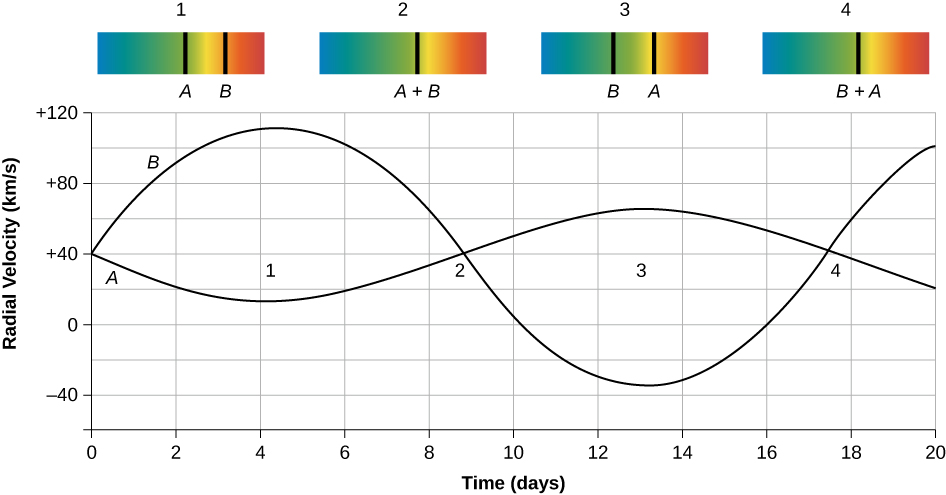
该动画允许你以两颗恒星质量的各种组合来跟踪双星系统的轨道。

来自双星轨道的质量

我们可以使用牛顿对开普勒第三定律的重新公式（在牛顿的万有引力定律中进行了讨论）来估计双星系统的质量。 开普勒发现，根据特定的数学公式，行星绕太阳运行所需的时间与其与太阳的距离有关。 在我们的双星情况下，如果两个物体相互旋转，那么根据这个方程，它们相互绕的周期 (\(P\)\(D\)) 与一个物体相对于另一个轨道的半长轴 () 有关

\[D^3= \left( M_1+M_2 \right) P^2 \nonumber\]

其\(D\)中，以天文单位表示，\(P\)以年为单位测量，\(M_1 + M_2\)是两颗恒星质量的总和，以太阳质量为单位。 对于天文学家来说，这是一个非常有用的公式；它说，如果我们能够在二进制系统中观察轨道的大小和恒星相互旋转的周期，我们就能计算出它们的质量之和。

大多数光谱二进制文件的周期从几天到几个月不等，其成员恒星之间的间隔通常小于 1 AU。 回想一下，非盟是指从地球到太阳的距离，所以这是一个很小的间隔，在恒星的距离上很难看见。 这就是为什么只有通过仔细研究其光谱才知道其中许多系统是双倍的原因。

我们可以分析径向速度曲线（如图中的曲线\(\PageIndex{4}\)），以确定光谱二进制中恒星的质量。 这在实践中很复杂，但原则上并不难。 我们通过多普勒效应测量恒星的速度。 然后，我们根据速度曲线确定周期，即恒星穿越轨道周期需要多长时间。 知道恒星移动的速度和它们需要多长时间才能告诉我们轨道的周长，从而可以告诉我们恒星的间隔（以千米或天文单位为单位）。 根据开普勒定律，周期和分离使我们能够计算出恒星质量的总和。

当然，知道质量之和不如单独知道每颗恒星的质量那么有用。 但是两颗恒星的相对轨道速度可以告诉我们每颗恒星的总质量有多少。 正如我们在跷跷板类比中看到的那样，质量越大的恒星离质心越近，因此轨道越小。 因此，与距离更远、质量更低的恒星相比，它在同一时间四处走动的速度更慢。 如果我们计算出相对于彼此的速度，我们就可以计算出相对于彼此的质量。 实际上，我们还需要知道二进制系统在天空中是如何朝向我们的视线方向的，但是如果我们这样做了，并且刚才描述的步骤是仔细执行的，结果就是计算出系统中两颗恒星中每颗恒星的质量。

总而言之，对两颗恒星围绕共同质心的运动进行很好的测量，再加上重力定律，使我们能够确定此类系统中恒星的质量。 这些质量测量对于发展恒星如何演变的理论绝对至关重要。 这种方法的最好之处之一是它与二进制系统的位置无关。 它同样适用于距离我们 100 光年的恒星，也适用于我们附近的恒星。

举个具体的例子，小天狼星是附录 J 中为数不多的我们有足够信息可以应用开普勒第三定律的双星之一：

\[D^3= \left( M_1+M_2 \right) P^2 \nonumber\]

在这种情况下，这两颗恒星，我们通常称之为小天狼星及其非常微弱的同伴，相隔约20 AU，轨道周期约为 50 年。 如果我们将这些值放在公式中，我们就有

\[\begin{array}{l} (20)^3= \left( M_1+M_2 \right) (50)^2 \\ 8000= \left( M_1+M_2 \right) (2500) \end{array} \nonumber\]

这可以用质量之和来求解：

\[M_1+M_2= \frac{8000}{2500}=3.2 \nonumber\]

因此，天狼星二进制系统中两颗恒星的质量总和是太阳质量的3.2倍。 为了确定每颗恒星的个体质量，我们需要两颗恒星的速度和轨道相对于视线的方向。

恒星质量范围

一颗恒星的质量能有多大？ 比太阳还大的恒星很少见。 距离太阳 30 光年以内的恒星的质量都不超过太阳的四倍。 在离太阳很远的地方进行搜索后，发现了几颗质量高达太阳100倍的恒星，而少数恒星（几十亿颗中的几颗）的质量可能高达250个太阳质量。 但是，大多数恒星的质量都小于太阳。

根据理论计算，一颗真正的恒星所能拥有的最小质量约为太阳的1/12。 天文学家所说的 “真正的” 恒星是指一颗热到足以融合质子形成氦气的恒星（正如《太阳：核强国》中所述）。 质量大约在太阳的1/100到1/12之间的物体可能会通过涉及氘的核反应在短时间内产生能量，但它们的热度不足以融合质子。 此类物体的质量介于恒星和行星之间，被命名为褐矮星（图\(\PageIndex{5}\)）。 褐矮星的半径与木星相似，但其质量比木星的质量大约13至80倍。 ²

人物猎户座中的\(\PageIndex{5}\)褐矮星。

这些由哈勃太空望远镜拍摄的图像显示了名为猎户座星云的恒星形成区域内梯形星团周围的区域。 (a) 在可见光图像中看不到褐矮星，这既是因为它们在可见光中发出的光很少，也是因为它们隐藏在该区域的尘埃云中。 (b) 这张照片是在红外光下拍摄的，红外光可以通过尘埃传递给我们。 这张照片中最微弱的物体是褐矮星，其质量是木星质量的13到80倍。 （来源 a：美国宇航局、C.R. O'Dell 和 S.K. Wong（莱斯大学）；来源 b：美国宇航局；K.L. Luhman（哈佛-史密森尼天体物理学中心）和 G. Schneider、E. Young、G. Rieke、R. Thompson（管家天文台））

质量小于太阳质量大约 1/100（或 10 个木星质量）的较小物体被称为行星。 它们可以辐射其所含放射性元素产生的能量，也可能辐射在自身重量下缓慢压缩产生的热量（这种过程称为引力收缩）。 但是，它们的内部温度永远不会达到足以发生任何核反应的高度。 例如，木星的质量约为太阳质量的1/1000，毫无疑问是一颗行星。 直到20世纪90年代，我们只能在自己的太阳系中探测到行星，但现在我们在其他地方也有成千上万的行星。 （我们将在《恒星的诞生和太阳系外行星的发现》中讨论这些激动人心的观测结果。）

质量与亮度的关系

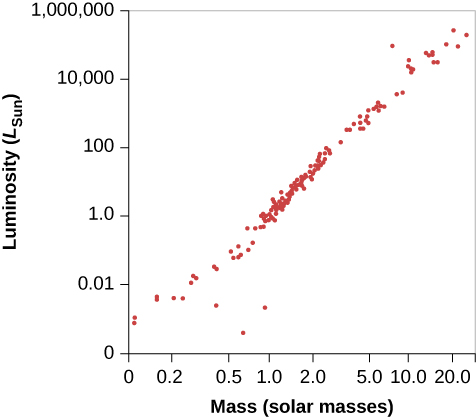
现在我们已经测量了许多不同类型的恒星的特征，我们可以搜索这些特征之间的关系。 例如，我们可以问一颗恒星的质量和亮度是否相关。 事实证明，对于大多数恒星来说，它们是：质量越大的恒星通常也越发亮。 这种关系被称为质量-亮度关系，如图所示\(\PageIndex{6}\)。 每个点代表一颗恒星，其质量和亮度均已知。 图表上的水平位置显示恒星的质量，以太阳的质量为单位给出，垂直位置以太阳的亮度为单位显示其亮度。

图：\(\PageIndex{6}\)质量-亮度关系。 标绘点显示了恒星的质量和亮度。 位于点序列下方的三个点都是白矮星。

我们也可以用数学术语说这句话。

\[L \sim M^{3.9} \nonumber\]

可以说，亮度（以太阳的亮度单位表示）随质量的第四次功率（以太阳质量为单位）而变化，这是一个相当不错的近似值。 （符号 ~ 表示两个量成比例。） 如果两颗恒星的质量相差为2倍，则质量较大的恒星将为2 ⁴，或亮度约为16倍；如果一颗恒星的质量是另一颗恒星的1/3，则其发光度将降低大约81倍。

示例\(\PageIndex{1}\)：根据恒星的亮度计算质量

可以重写质量亮度公式，以便在已知亮度的情况下确定质量值。

解决方案

首先，我们必须以太阳的质量和亮度为单位来表示恒星的质量和亮度，从而使单位正确：

\[L/L_{\text{Sun}}= \left( M/M_{\text{Sun}} \right)^4 \nonumber\]

现在我们可以取两边的第四个根，这相当于让双方都达到 1/4 = 0.25 的功率。 在这种情况下，公式为：

\[M/M_{\text{Sun}} = \left( L/L_{\text{Sun}} \right)^{0.25}= \left(L/L_{\text{Sun}} \right)^{0.25} \nonumber\]

练习\(\PageIndex{1}\)

在上一节中，我们使用开普勒第三定律将天狼星二进制系统（天狼星及其微弱同伴）中两颗恒星的质量之和确定为 3.2 个太阳质量。 使用质量-亮度关系，计算每颗恒星的质量。

回答

在附录J中，天狼星的亮度是太阳的23倍。 可以将该值插入到质量亮度关系中以获得 Sirius 的质量：\(M/M_{\text{Sun}}=23^{0.25}=2.2\)

然后，天狼星的同伴恒星的质量就是\(3.2 – 2.2 = 1.0\)太阳质量。

注意这种质量与亮度的关系有多好。 大多数恒星（见图\(\PageIndex{6}\)）都沿着一条线落下，从图的左下角（低质量，低亮度）一直延伸到右上角（高质量，高亮度）角。 大约 90% 的恒星服从质量-亮度关系。 稍后，我们将探讨为什么存在这种关系，以及我们可以从大约 10% 的 “违抗” 这种关系的恒星那里学到什么。

关键概念和摘要

恒星的质量可以通过分析双星的轨道来确定，双星是绕共同质心运行的两颗恒星。 在视觉二进制文件中，两颗恒星可以在望远镜中分别看到，而在光谱二进制文件中，只有光谱显示了两颗恒星的存在。 恒星质量的范围从大约1/12到超过太阳质量的100倍不等（在极少数情况下，达到太阳质量的250倍）。 质量在太阳质量的1/12和1/100之间的物体被称为褐矮星。 不能发生核反应的物体是行星。 在大多数情况下，质量最大的恒星也是最亮的恒星，这种关联被称为质量-亮度关系。

脚注

¹ 在我们写这本书时，行星和褐矮星之间的分界线的确切位置是天文学家争论的话题（事实上，每个天体的确切定义也是如此）。 即使是那些接受氘聚变（见《恒星的诞生和太阳系以外的行星的发现》）作为褐矮星面临的关键问题的人也承认，根据恒星的组成和其他因素，这种矮星的最低质量可能在11到16个木星质量之间。

词汇表

双星

两颗相互旋转的恒星

褐矮星

大小介于行星和恒星之间的物体；大约质量范围从太阳质量的1/100到自我维持的核反应的质量下限（约为太阳质量的1/12）

质量与亮度的关系

观测到的许多（占所有恒星的90％）的质量和亮度之间的关系

光谱二进制

一颗双星，其分量未被解析，但其二进制性质由径向速度的周期性变化表示，表示轨道运动

视觉二进制

一颗双星，其中的两个组成部分通过望远镜分辨出来