8.7:求解比例和相似图应用程序
- Page ID
- 204749
在本节结束时,您将能够:
- 求解比例
- 求解相似图形的应用程序
求解比例
当两个有理表达式相等时,将它们关联的方程称为比例。
比例是形式的方程式\(\dfrac{a}{b}=\dfrac{c}{d}\),其中\(b \ne 0\),\(d \ne 0\)。
比例读作 “a 对 b,如同 c 对 d”
方程式\(\dfrac{1}{2}=\dfrac{4}{8}\) is a proportion because the two fractions are equal.
比例读\(\dfrac{1}{2}=\dfrac{4}{8}\)作 “1 等于 2 就像 4 等于 8”。
在许多应用程序中,比例用来 “放大” 数量。 我们将从一个非常简单的例子开始,这样你就可以看到比例是如何工作的。 即使你能马上找出这个例子的答案,也要确保你也学会用比例求解。
假设一位学校校长想让 1 位老师为 20 名学生服务。 她可以使用比例来计算60名学生的教师人数。 我们假设 x 是 60 名学生的教师人数,然后设置比例:
\[\dfrac{1\,\text{teacher}}{20\,\text{students}}=\dfrac{x\,\text{teachers}}{60\,\text{students}}\nonumber\]
我们谨慎地匹配分子的单位和分母的单位——分子中的老师,分母中的学生。
由于比例是带有有理表达式的方程,因此我们将以与求解有理方程式中的方程相同的方式求解比例。 我们将方程的两边乘以 LCD 以清除分数,然后求解由此产生的方程。
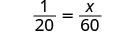 |
|
| 将两边乘以液晶屏,60。 | 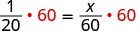 |
| 简化。 | 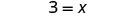 |
| 60名学生需要3名老师。 |
现在我们将举几个例子来求解没有任何单位的数值比例。 然后,我们将使用比例求解应用程序。
\(\dfrac{x}{63}=\dfrac{4}{7}\)。
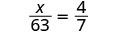 |
||
| 要分离 x,请将两边乘以 LCD,即 63。 | 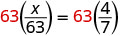 |
|
| 简化。 | 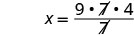 |
|
| 除以常见因素。 | 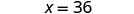 |
|
| 查看。 为了检查我们的答案,我们用原来的比例代替。 | ||
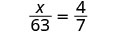 |
||
 |
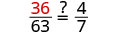 |
|
| 显示常见因素。 | 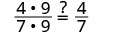 |
|
| 简化。 | 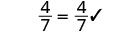 |
\(\dfrac{n}{84}=\dfrac{11}{12}\)。
- 回答
-
77
\(\dfrac{y}{96}=\dfrac{13}{12}\)。
- 回答
-
104
\(\dfrac{144}{a}=\dfrac{9}{4}\)。
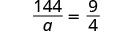 |
||
| 将两边乘以液晶屏。 | 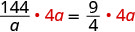 |
|
| 删除双方的共同因素。 | 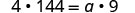 |
|
| 简化。 | 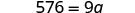 |
|
| 将两边除以 9。 | 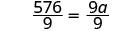 |
|
| 简化。 | 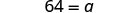 |
|
| 查看。 | ||
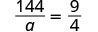 |
||
 |
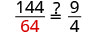 |
|
| 显示常见因素。 | 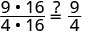 |
|
| 简化。 | 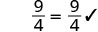 |
\(\dfrac{91}{b}=\dfrac{7}{5}\)。
- 回答
-
65
\(\dfrac{39}{c}=\dfrac{13}{8}\)。
- 回答
-
24
\(\dfrac{n}{n+14}=\dfrac{5}{7}.\)
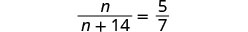 |
||
| 将两边乘以液晶屏。 | 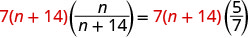 |
|
| 删除双方的共同因素。 | 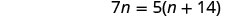 |
|
| 简化。 | 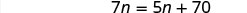 |
|
| 求解 n。 | 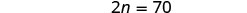 |
|
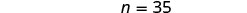 |
||
| 查看。 | ||
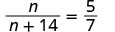 |
||
 |
 |
|
| 简化。 | 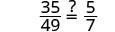 |
|
| 显示常见因素。 | 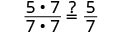 |
|
| 简化。 |  |
\(\dfrac{y}{y+55}=\dfrac{3}{8}\)。
- 回答
-
33
\(\dfrac{z}{z−84}=−\dfrac{1}{5}\)。
- 回答
-
14
\(\dfrac{p+12}{9}=\dfrac{p−12}{6}\)。
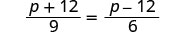 |
||
| 将两边乘以液晶屏,18。 |  |
|
| 简化。 |  |
|
| 分发。 | 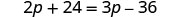 |
|
| 求解 p。 | 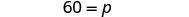 |
|
| 查看。 | ||
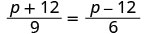 |
||
 |
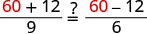 |
|
| 简化。 | 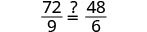 |
|
| 除以。 | 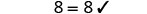 |
\(\dfrac{v+30}{8}=\dfrac{v+66}{12}\)。
- 回答
-
42
\(\dfrac{2x+15}{9}=\dfrac{7x+3}{15}\)。
- 回答
-
6
为了按比例求解应用程序,我们将遵循通常的求解应用程序策略。 但是当我们设置比例时,我们必须确保单位正确——分子中的单位必须匹配,分母中的单位必须匹配。
当儿科医生给孩子开对乙酰氨基酚处方时,他们会为孩子每体重25磅开5毫升(ml)的对乙酰氨基酚处方。 如果佐伊体重 80 磅,她的医生会开多少毫升的对乙酰氨基酚处方?
| 确定我们要查找的内容,然后选择一个变量来表示它。 | 医生会开多少毫升的对乙酰氨基酚? |
| 让 a=ml 对乙酰氨基酚。 | |
| 写一句话,给出找到它的信息。 | 如果每 25 磅开出 5 毫升处方,那么 80 磅的处方是多少? |
换算成比例——小心单位。 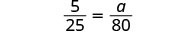 |
|
| 将两边乘以液晶屏 400。 | 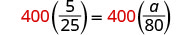 |
| 删除双方的共同因素。 | 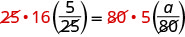 |
| 简化,但不要在左边乘以。 注意下一步将是什么。 | 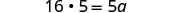 |
| 求解 a. | 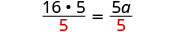 |
| 查看。 | 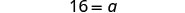 |
| 答案合理吗? | |
| 是的,因为80大约是25的3倍,所以药物应该是大约3乘以5。 所以 16 毫升是有道理的。 | |
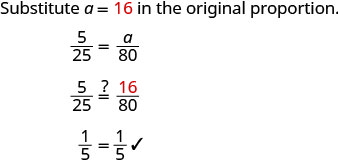 |
|
| 写一个完整的句子。 | 儿科医生会给佐伊开16毫升的对乙酰氨基酚处方。 |
儿科医生为孩子每体重 25 磅开出 5 毫升(ml)的对乙酰氨基酚处方。 医生会为体重60磅的艾米莉亚开多少毫升的对乙酰氨基酚处方?
- 回答
-
12 毫升
每增加一个孩子的体重 1 千克(kg),儿科医生就会开出 15 毫克(mg)的减烧剂。 如果伊莎贝拉体重12千克,儿科医生会开多少毫克的减烧药?
- 回答
-
180 毫升
一个 16 盎司的冰焦糖玛奇朵含有 230 卡路里的热量。 一个 24 盎司的冰焦糖玛奇朵里有多少卡路里?
| 确定我们要查找的内容,然后选择一个变量来表示它。 | 一个 24 盎司的冰焦糖玛奇朵里有多少卡路里? |
| 让 c=24 盎司的卡路里。 | |
| 写一句话,给出找到它的信息。 | 如果 16 盎司中有 230 卡路里,那么 24 盎司中有多少卡路里? |
换算成比例——小心单位。 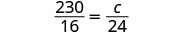 |
|
| 将两边乘以液晶屏,48。 | 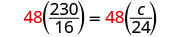 |
| 删除双方的共同因素。 | 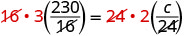 |
| 简化。 | 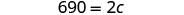 |
| 求解 c。 | 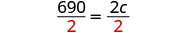 |
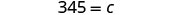 |
|
| 查看。 | |
| 答案合理吗? | |
| 是的,24 盎司的 345 卡路里等于 16 盎司超过 290 卡路里,但不会超过 290 卡路里。 | |
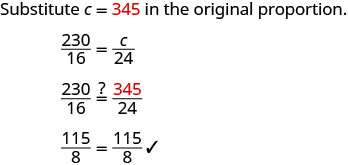 |
|
| 写一个完整的句子。 | 一个 24 盎司的冰焦糖玛奇朵含有 345 卡路里的热量。 |
在快餐店,一杯22盎司的巧克力奶昔含有850卡路里的热量。 他们的 12 盎司巧克力奶昔中有多少卡路里? 将答案四舍五入到最接近的整数。
- 回答
-
464 卡路里
Yaneli 喜欢 Starburst 糖果,但想让她的零食保持在 100 卡路里的热量。 如果 8 块糖果有 160 卡路里的热量,那么她的零食里能含多少卡路里?
- 回答
-
5 件
约西亚去墨西哥度过春假,将325美元兑换成墨西哥比索。 当时,汇率为1美元等于12.54墨西哥比索。 他这次旅行得到了多少墨西哥比索?
| 你要找什么? | 约西亚得到多少墨西哥比索? |
| 分配一个变量。 | 假设 p = 墨西哥比索的数量。 |
| 写一句话,给出找到它的信息。 | 如果1美元等于12.54墨西哥比索,那么325美元是多少比索? |
|
换算成比例——小心单位。
|
|
| 将两边乘以液晶屏,12.54p。 | 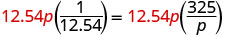 |
| 删除双方的共同因素。 | 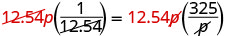 |
| 简化。 | 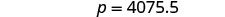 |
| 查看。 | |
| 答案合理吗? | |
| 是的,100美元等于1,254比索。325美元略高于这个数额的3倍,所以我们的4075.5比索的答案是有道理的。 | |
 |
|
| 写一个完整的句子。 | 约西亚的春假旅行得到了 4075.5 比索。 |
尤里安娜要去欧洲,想把800美元兑换成欧元。 按照当前汇率,1 美元等于 0.738 欧元。 她的旅行会有多少欧元?
- 回答
-
590.4 欧元
科里和妮可正在日本旅行,需要将600美元兑换成日元。 如果每美元是94.1日元,他们会得到多少日元?
- 回答
-
56,460 日元
在上面的示例中,我们使用比例将比索的数量与美元数联系起来。 我们可以说比索的数量与美元数成正比。 如果两个量按比例相关,我们说它们是成比例的。
求解相似图形应用程序
当你在手机或平板电脑上缩小或放大照片,在地图上计算出一段距离,或者使用图案制作书柜或缝制衣服时,你正在处理相似的人物。 如果两个数字的形状完全相同,但大小不同,则说它们是相似的。 一个是另一个的比例模型。 它们的所有对应角度都具有相同的测量值,并且它们对应的边的比例相同。
如果两个图对应角度的测量值相等,并且它们对应的边的比例相同,则这两个数字是相似的。
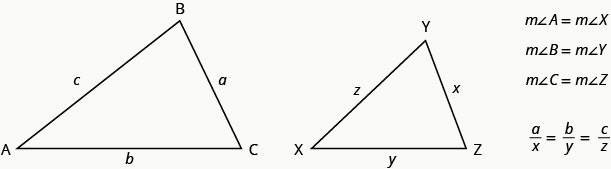
例如,图中的两个三角形是相似的。 ΔABC 的每一边长度是 ΔXYZ 相应边长度的 4 倍。
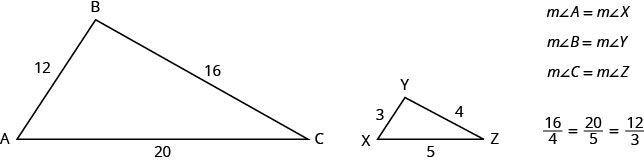
相似三角形的属性对此进行了总结。
如果 ΑABC 与 ΔXYZ 相似
为了求解具有相似图形的应用程序,我们将遵循我们之前使用的几何应用程序问题解决策略。
- 阅读问题并使所有的单词和想法都被理解。 画出图形并用给定的信息标记它。
- 确定我们在寻找什么。
- 通过选择一个变量来表示我们要找的东西来@@ 命名它。
- 通过编写适合情况的公式或模型将其@@ 转换为方程。 在给定的信息中替换。
- 使用良好的代数技巧求@@ 解方程。
- 检查问题中的答案并确保答案合理。
- 用完整的句子@@ 回答问题。
△ABC 与 ΔXYZ 类似
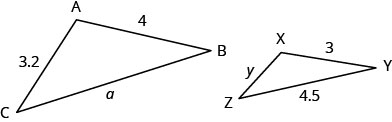
| 第 1 步。 阅读问题。 画出图形并用给定的信息标记它。 | 给出了数字。 |
| 第 2 步。 确定我们在寻找什么。 | 相似三角形边的长度。 |
| 第 3 步。 为变量命名。 |
假设 a= △ABC 第三边的长度。 y= △XYZ 第三边的长度。 |
| 第 4 步。 翻译。 | 由于三角形相似,因此相应的边是成比例的。 |
| 我们需要写一个方程式,将我们要找的边和已知的比率进行比较。 由于侧面 AB = 4 对应于我们所知道的 XY = 3 边\(\dfrac{AB}{XY}=\dfrac{4}{3}\)。 所以我们用方程\(\dfrac{AB}{XY}\)来找出我们要找的边。 注意正确匹配相应的双面。 | \(\dfrac{AB}{XY}=\dfrac{BC}{YZ}=\dfrac{AC}{XZ}\)。  |
| 替代。 | 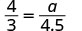 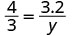 |
| 第 5 步。 求解方程。 |
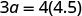
|
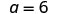 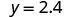 |
|
| 第 6 步。 查看。 | |
| 第 7 步。 回答问题。 | ΑABC 的第三面是 6,ΔXYZ 的第三面是 2.4。 |
△ABC 与 ΔXYZ 类似。 图中给出了每个三角形两边的长度。
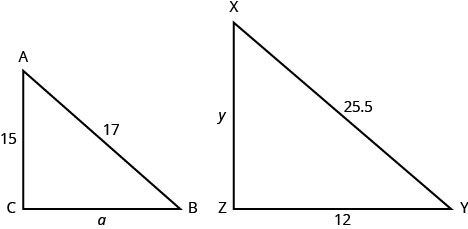
找出 a 边的长度
- 回答
-
8
△ABC 与 ΔXYZ 类似。 图中给出了每个三角形两边的长度。
- 回答
-
22.5
在地图上,旧金山、拉斯维加斯和洛杉矶形成一个三角形,其边如下图所示。 如果洛杉矶到拉斯维加斯的实际距离为 270 英里,请找出从洛杉矶到旧金山的距离。
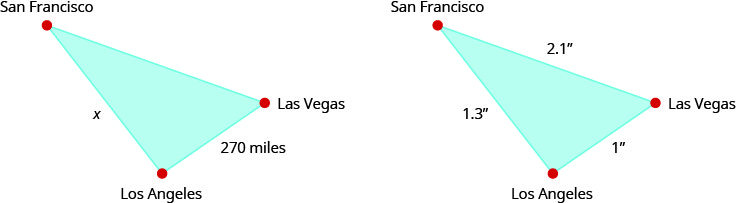
| 阅读问题。 用给定的信息绘制图形和标签。 | 数字如上所示。 |
| 确定我们在寻找什么。 | 从洛杉矶到旧金山的实际距离。 |
| 为变量@@ 命名。 | 让 x= 从洛杉矶到旧金山的距离。 |
| 翻译成方程式。 由于三角形 相似,因此相应的边是 成比例的。 我们将分子 “英里”,将分母设为 “英寸”。 |
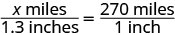 |
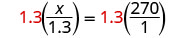 |
|
| 求解方程。 | 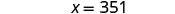 |
| 查看。 | |
| 在地图上,从洛杉矶到 旧金山的距离大于 洛杉矶到拉斯维加斯的距离。 由于 351 大 于 270,所以答案是有道理的。 |
|
 |
|
| 回答问题。 | 从洛杉矶到旧金山的距离为 351 英里。 |
在地图上,西雅图、波特兰和博伊西形成一个三角形,其边如下图所示。 如果从西雅图到博伊西的实际距离为 400 英里,请计算从西雅图到波特兰的距离。
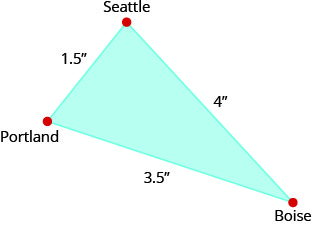
- 回答
-
150 英里
使用上面的地图,找到从波特兰到博伊西的距离。
- 回答
-
350 英里
我们可以使用相似的数字来找到我们无法直接测量的高度。
泰勒身高 6 英尺。 一天下午晚些时候,他的影子长达 8 英尺。 同时,一棵树的阴影长达 24 英尺。 找出树的高度。
| 阅读问题并画一个数字。 | 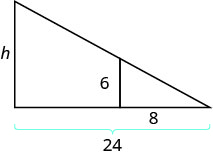 |
| 我们正在寻找 h,树的高度。 | |
| 我们将使用相似的三角形来写一个方程。 | |
| 小三角形类似于大三角形。 | 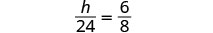 |
| 求解比例。 | 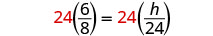 |
| 简化。 | 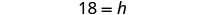 |
| 查看。 | |
|
泰勒的高度小于他阴影的长度,所以树的高度小于其阴影的长度是有道理的。 |
|
 |
电线杆投射出 50 英尺长的阴影。 在附近,一个 8 英尺高的交通标志投射出 10 英尺长的阴影。 电线杆有多高?
- 回答
-
40 英尺
一棵松树在一座30英尺高的建筑物旁边投射出80英尺的阴影,该建筑投射了40英尺的阴影。 那棵松树有多高?
- 回答
-
60 英尺
关键概念
- 相似三角形的属性
- 如果 ΑABC 与 ΔXYZ 相似
- 几何应用的问题解决策略
- 阅读问题并确保所有文字和想法都被理解。 画出图形并用给定的信息标记它。
- 确定我们在寻找什么。
- 通过选择一个变量来表示我们要找的东西来@@ 命名它。
- 通过编写适合情况的公式或模型将其@@ 转换为方程。 在给定的信息中替换。
- 使用良好的代数技巧求@@ 解方程。
- 检查问题中的答案并确保答案合理。
- 用完整的句子@@ 回答问题。
词汇表
- 比例
- 比例是形式为 “” 的方程\(\dfrac{a}{b}=\dfrac{c}{d}, where \(b \ne 0\)式\(d \ne 0\)。 该比例读作 “a 对 b c 等于 d”。
- 相似的数字
- 如果两个图对应角度的测量值相等,并且它们对应的边的比例相同,则这两个数字是相似的。