8.1: 简化有理表达式
- Page ID
- 204847
在本节结束时，您将能够：
- 确定未定义有理表达式的值
- 评估有理表达式
- 简化有理表达式
- 使用相反因子简化有理表达式
在第 1 章中，我们回顾了分数的属性及其运算。 我们引入了有理数，它们只是分数，其中分子和分母是整数，分母不为零。
在本章中，我们将研究分子和分母是多项式的分数。 我们称这些为理性表达。
有理表达式是这种形式的表达式\(\frac{p(x)}{q(x)}\)，其中 p 和 q 是多项式，\(q \ne 0\).
以下是一些有理表达式的例子：
\[\begin{array}{cccc} {−\frac{13}{42}}&{\frac{7y}{8z}}&{\frac{5x+2}{x^2−7}}&{\frac{4x^2+3x−1}{2x−8}}\\ \nonumber \end{array}\]
请注意，上面列出的第一个有理表达式只是一个分数。\(−\frac{13}{42}\) 由于常量是零度的多项式，因此只要分母不为零，两个常量的比率就是有理表达式。
我们将使用有理表达式执行与分数相同的运算。 我们将对它们进行简化、加、减、乘、除并在应用程序中使用。
确定未定义有理表达式的值
当我们处理数字分数时，很容易避免除以零，因为我们可以在分母中看到数字。 为了避免在有理表达式中除以零，我们决不能允许将使分母变为零的变量的值。
如果分母为零，则有理表达式未定义。 有理表达式的分子可能为 0，但不是分母。
因此，在我们开始使用有理表达式进行任何运算之前，我们首先对其进行检查以找到将使分母为零的值。 这样，例如，当我们求解有理方程时，我们就会知道我们找到的代数解是否允许。
- 将分母设置为零。
- 如果可能，求解实数集中的方程。
确定未定义有理表达式的值：
- \(\frac{9y}{x}\)
- \(\frac{4b−3}{2b+5}\)
- \(\frac{x+4}{x^2+5x+6x}\)
解决方案
当分母为零时，表达式将未定义。
| 1。 | \(\frac{9y}{x}\) |
| 将分母设置为零。 求解变量。 | x=0 |
| \(\frac{9y}{x}\)为 x=0 未定义。 | |
| 2。 |
\(\frac{4b−3}{2b+5}\) |
| 将分母设置为零。 求解变量。 | 2b+5=0 |
| 2b=−5 | |
| \(b=−\frac{5}{2}\) | |
| \(\frac{4b−3}{2b+5}\)未定义为\(b=−\frac{5}{2}\)。 | |
| 3。 | \(\frac{x+4}{x^2+5x+6x}\) |
| 将分母设置为零。 求解变量。 | \(x^2+5x+6x=0\) |
| \((x+2)(x+3)=0\) | |
| x+2=0 或 x+3=0 | |
| x=−2 或 x=−3 | |
| \(\frac{x+4}{x^2+5x+6x}\)为 x=−2 或 x=−3 未定义。 |
说 x=−2orx=−3 的有理表达式\(\frac{x+4}{x^2+5x+6x}\)未定义，类似于在竞赛规则中写下 “禁止的地方无效” 一词。
试试看\(\PageIndex{2}\)
确定未定义有理表达式的值：
- \(\frac{3y}{x}\)
- \(\frac{8n−5}{3n+1}\)
- \(\frac{a+10}{a^2+4a+3a}\)
- Answer
-
- x=0
- \(n=−\frac{1}{3}\)
- a=−1, a=−3
Try It \(\PageIndex{3}\)
确定未定义有理表达式的值：
- \(\frac{4p}{5q}\)
- \(\frac{y−1}{3y+2}\)
- \(\frac{m−5}{m^2+m−6}\)
- 回答
-
- q=0
- \(y=−\frac{2}{3}\)
- m=2，m=−3
评估有理表达式
为了评估有理表达式，我们将变量的值替换为表达式并进行简化，就像我们在本书中对许多其他表达式所做的那样。
\(\frac{2x+3}{3x−5}\)对每个值进行评估：
- x=0
- x=2
- x=−3
解决方案
| 1。 |  |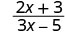
 |
 |
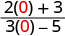| 简化。 |  |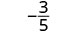
| 2。 |  |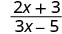
 |
 |
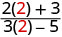| 简化。 |  |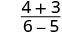
 |
|
 |
|
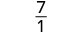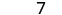| 3。 |  |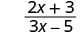
 |
 |
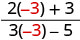| 简化。 |  |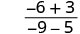
 |
|
 |
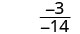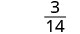试试看\(\PageIndex{5}\)
评估\(\frac{y+1}{2y−3}\) for each value:
- y=1
- y=−3
- y=0
- Answer
-
- −2
- \(\frac{2}{9}\)
- \(−\frac{1}{3}\)
Try It \(\PageIndex{6}\)
\(\frac{5x−1}{2x+1}\)对每个值进行评估：
- x=1
- x=−1
- x=0
- 回答
-
- \(\frac{4}{3}\)
- 6
- −1
\(\frac{x^2+8x+7}{x^2−4}\)对每个值进行评估：
- x=0
- x=2
- x=−1
解决方案
| 1。 |  |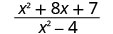
 |
 |
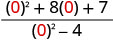| 简化。 |  |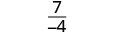
 |
|
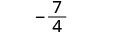| 2。 | |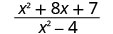
 |
 |
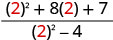| 简化。 |  |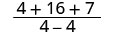
 |
|
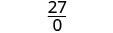| 对于 x = 2，这个有理表达式是未定义的。 | |
| 3。 |  |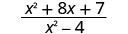
 |
 |
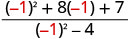| 简化。 |  |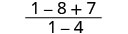
 |
|
 |
|
 |
|
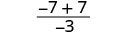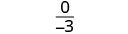试试看\(\PageIndex{8}\)
评估\(\frac{x^2+1}{x^2−3x+2}\) for each value:
- x=0
- x=−1
- x=3
- Answer
-
- \(\frac{1}{2}\)
- \(\frac{1}{3}\)
- 2
Try It \(\PageIndex{9}\)
\(\frac{x^2+x−6}{x^2−9}\)对每个值进行评估。
- x=0
- x=−2
- x=1
- 回答
-
- \(\frac{2}{3}\)
- \(\frac{4}{5}\)
- \(\frac{1}{2}\)
请记住，如果分数的分子和分母中除了 1 之外没有其他公共因子，则分数是简化的。 当我们评估有理表达式时，我们要确保简化生成的分数。
\(\frac{a^2+2ab+b^2}{3ab}\)对每个值进行评估。
- a=1，b=2
- a=−2，b=−1
- \(a=\frac{1}{3}\)，b=0
解决方案
| 1。 | \(\frac{a^2+2ab+b^2}{3ab}\)当 a=1 时，b=2 |
 |
 |
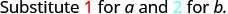| 简化。 |  |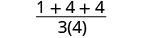
 |
|
 |
|
| 2。 | \(\frac{a^2+2ab+b^2}{3ab}\)当 a=−2 时，b=−1 |
 |
 |
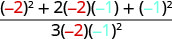| 简化。 |  |
 |
|
 |
|
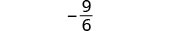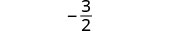| 3。 | \(\frac{a^2+2ab+b^2}{3ab}\)什么时候\(a=\frac{1}{3}\)，b=0 |
 |
 |
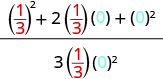| 简化。 |  |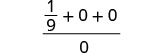
 |
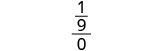试试看\(\PageIndex{11}\)
评估\(\frac{2a^{3}b}{a^2+2ab+b^2}\) for each value.
- a=−1, b=2
- a=0, b=−1
- a=1, \(b=\frac{1}{2}\)
- Answer
-
- −4
- 0
- \(\frac{4}{9}\)
Try It \(\PageIndex{12}\)
\(\frac{a^2−b^2}{8ab^3}\)对每个值进行评估：
- a=1，b=−1
- \(a=\frac{1}{2}\), b=−1
- a=−2，b=1
- 回答
-
- 0
- \(\frac{3}{16}\)
- \(\frac{3}{16}\)
简化有理表达式
就像分数的分子和分母中除了 1 之外没有其他公共因子时被视为简化一样，如果有理表达式的分子和分母中除了 1 之外没有其他共同因子，则该有理表达式也被简化了。
如果有理表达式的分子和分母中没有共同的因子，则认为有理表达式是简化的。
例如：
- \(\frac{2}{3}\)之所以简化，是因为没有 2 和 3 的常见因子。
- \(\frac{2x}{3x}\)未简化，因为 x 是 2 x 和 3 x 的常用因子。
我们使用等效分数属性来简化数字分数。 我们在这里重述一下，因为我们还将使用它来简化有理表达。
如果 a、b 和 c 是数字\(b \ne 0\)，其中、\(c\ne 0\)、然后\(\frac{a}{b}=\frac{a·c}{b·c}\)和\(\frac{a·c}{b·c}=\frac{a}{b}\)
请注意，在等效分数属性中，明确禁止使用会使分母为零的值。 我们明白了\(b \ne 0\)，说得\(c\ne 0\)很清楚。 每次我们写一个有理表达式时，我们都应该做一个类似的声明，不允许使用会使分母为零的值。 但是，为了让我们专注于手头的工作，我们将省略将其写在示例中。
让我们先回顾一下如何简化数字分数。
简化：\(−\frac{36}{63}\)。
解决方案
 |
|
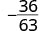| 重写显示常见因子的分子和分母。 |  |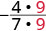
| 使用等效分数属性进行简化。 |  |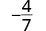
请注意，分数\(−\frac{4}{7}\)已简化，因为不再有常见因子。
试试看\(\PageIndex{14}\)
简化：\(−\frac{45}{81}\).
- Answer
-
\(−\frac{5}{9}\)
Try It \(\PageIndex{15}\)
简化：\(−\frac{42}{54}\)。
- 回答
-
\(−\frac{7}{9}\)
在本章中，我们将假设所有使分母为零的数值都被排除在外。 我们不会为每个有理表达式写出限制，但请记住，分母永远不能为零。 因此，在下一个示例中，\(x \ne 0\)和\(y \ne 0\)。
简化：\(\frac{3xy}{18x^{2}y^{2}}\)。
解决方案
 |
|
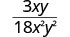| 重写显示常见因子的分子和分母。 |  |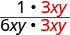
| 使用等效分数属性进行简化。 |  |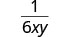
你有没有注意到这些步骤与我们在多项式中划分单项式时所采取的步骤相同？
试试看\(\PageIndex{17}\)
简化：\(\frac{4x^{2}y}{12xy^2}\).
- Answer
-
\(\frac{x}{3y}\)
Try It \(PageIndex{18}\)
简化：\(\frac{16x^{2}y}{2xy^2}\)。
- 回答
-
\(\frac{8x}{y}\)
在删除常见因素时要非常小心。 将因子乘以制成产品。 您可以从产品中移除因子。 您不能从总和中删除一个术语。
请注意，从\(\frac{x+5}{x}\)中移除 x 就像取消分数中的 2 一样\(\frac{2+5}{2}\)！
如何简化有理二项式
简化：\(\frac{2x+8}{5x+20}\)。
解决方案
试试看\(\PageIndex{20}\)
简化：\(\frac{3x−6}{2x−4}\).
- Answer
-
\(\frac{3}{2}\)
Try It \(\PageIndex{21}\)
简化：\(\frac{7y+35}{5y+25}\)。
- 回答
-
\(\frac{7}{5}\)
现在，我们总结了简化有理表达式时应遵循的步骤。
- 将分子和分母完全分解。
- 通过划分常见因素进行简化。
在以下示例中，我们将使用我们在分解中介绍的方法对分子和分母中的多项式进行分解。
简化：\(\frac{x^2+5x+6}{x^2+8x+12}\)。
解决方案
| \(\frac{x^2+5x+6}{x^2+8x+12}\) | |
| 系数分子和分母。 | \(\frac{(x+2)(x+3)}{(x+2)(x+6)}\) |
| 从分子和分母中移除公因子 x+2。 | \(\frac{x+3}{x+6}\) |
你能分辨出这个例子中必须排除 x 的哪些值吗？
试试看\(\PageIndex{23}\)
简化：\(\frac{x^2−x−2}{x^2−3x+2}\).
- Answer
-
\(\frac{x+1}{x−1}\)
Try It \(\PageIndex{24}\)
简化：\(\frac{x^2−3x−10}{x^2+x−2}\)。
- 回答
-
\(\frac{x−5}{x−1}\)
简化：\(\frac{y^2+y−42}{y^2−36}\)。
解决方案
| \(\frac{y^2+y−42}{y^2−36}\)。 | |
| 系数分子和分母。 | \(\frac{(y+7)(y−6)}{(y+6)(y−6)}\) |
| 从分子和分母中移除公因子 y−6。 | \(\frac{y+7}{y+6}\) |
试试看\(\PageIndex{26}\)
简化：\(\frac{x^2+x−6}{x^2−4}\).
- Answer
-
\(\frac{x+3}{x+2}\)
Try It \(\PageIndex{27}\)
简化：\(\frac{x^2+8x+7}{x^2−49}\)。
- 回答
-
\(\frac{x+1}{x−7}\)
简化：\(\frac{p^3−2p^2+2p−4}{p^2−7p+10}\)。
解决方案
| \(\frac{p^3−2p^2+2p−4}{p^2−7p+10}\) | |
| 分解分子和分母，使用分组来分解分子。 | \(\frac{p^2(p−2)+2(p−2)}{(p−5)(p−2)}\) |
| \(\frac{(p^2+2)(p−2)}{(p−5)(p−2)}\) | |
| 从分子和分母中移除公因子 p−2。 | \(\frac{p^2+2}{p−5}\) |
试试看\(\PageIndex{29}\)
简化：\(\frac{y^3−3y^2+y−3}{y^2−y−6}\).
- Answer
-
\(\frac{y^2+1}{y+2}\)
Try It \(\PageIndex{30}\)
简化：\(\frac{p^3−p^2+2p−2}{p^2+4p−5}\)。
- 回答
-
\(\frac{p^2+2}{p+5}\)
简化：\(\frac{2n^2−14n}{4n^2−16n−48}\)。
解决方案
| \(\frac{2n^2−14n}{4n^2−16n−48}\) | |
| 将分子和分母分数分解出来，首先分解出 GCF。 | \(\frac{2n(n−7)}{4(n^2−4n−12)}\) |
| \(\frac{2n(n−7)}{4(n−6)(n+2)}\) | |
| 移除共同因子 2。 | \(\frac{n(n−7)}{2(n−6)(n+2)}\) |
试试看\(\PageIndex{32}\)
简化：\(\frac{2n^2−10n}{4n^2−16n−20}\).
- Answer
-
\(\frac{n}{2(n+1)}\)
Try It \(\PageIndex{33}\)
简化：\(\frac{4x^2−16x}{8x^2−16x−64}\)。
- 回答
-
\(\frac{x}{2(x+2)}\)
简化：\(\frac{3b^2−12b+12}{6b^2−24}\)。
解决方案
| \(\frac{3b^2−12b+12}{6b^2−24}\) | |
| 将分子和分母分数分解出来，首先分解出 GCF。 | \(\frac{3(b^2−4b+4)}{6(b^2−4)}\) |
| \(\frac{3(b−2)(b−2)}{6(b−2)(b+2)}\) | |
| 移除 b−2 和 3 的常见因子。 | \(\frac{3(b−2)}{2(b+2)}\) |
试试看\(\PageIndex{35}\)
简化：\(\frac{2x^2−12x+18}{3x^2−27}\).
- Answer
-
\(\frac{2(x−3)}{3(x+3)}\)
Try It \(PageIndex{36}\)
简化：\(\frac{5y^2−30y+25}{2y^2−50}\)。
- 回答
-
\(\frac{5(x−1)}{2(x+5)}\)
简化：\(\frac{m^3+8}{m^2−4}\)。
解决方案
| \(\frac{m^3+8}{m^2−4}\) | |
| 使用立方和平方差的公式对分子和分母进行分数。 | \(\frac{(m+2)(m^2−2m+4)}{(m+2)(m−2)}\) |
| 移除 m+2 的常见因子。 | \(\frac{m^2−2m+4}{m−2}\) |
试试看\(\PageIndex{38}\)
简化：\(\frac{p^3−64}{p^2−16}\).
- Answer
-
\(\frac{p^2+4p+16}{p+4}\)
Try It \(\PageIndex{39}\)
简化：\(\frac{x^3+8}{x^2−4}\)。
- 回答
-
\(\frac{x^2−2x+4}{x−2}\)
使用相反因子简化有理表达式
现在我们将看到如何简化其分子和分母具有相反因子的有理表达式。 比如说，让我们从一个数值分数开始\(\frac{7}{−7}\)。
我们知道这个分数简化为 −1。 我们还认识到，分子和分母是相反的。
在 F ou ndations 中，我们引入了相反的表示法：a 的对立面是 −a。我们还记得 −a=−1·a
我们简化了分数\(\frac{a}{−a}\)
\[\begin{array}{ll} {}&{\frac{a}{−a}}\\ {\text{We could rewrite this.}}&{\frac{1·a}{−1·a}}\\ {\text{Remove the common factors.}}&{\frac{1}{−1}}\\ {\text{Simplify.}}&{−1}\\ \nonumber \end{array}\]
因此，用同样的方式，我们可以简化分数\(\frac{x−3}{−(x−3)}\)
\[\begin{array}{ll} {}&{\frac{x−3}{−(x−3)}}\\ {\text{We could rewrite this.}}&{\frac{1·(x−3)}{−1·(x−3)}}\\ {\text{Remove the common factors.}}&{\frac{1}{−1}}\\ {\text{Simplify.}}&{−1}\\ \nonumber \end{array}\]
但是 x−3 的反面可以用不同的写法：
\[\begin{array}{ll} {}&{−(x−3)}\\ {\text{Distribute.}}&{−x+3}\\ {\text{Rewrite.}}&{3−x}\\ \nonumber \end{array}\]
这意味着分数\(\frac{x−3}{3−x}\)简化为 −1。
一般来说，我们可以将与 a−b 相反的词写成 b−a。因此，有理表达式\(\frac{a−b}{b−a}\)简化为 −1。
a−b 的反面是 b−a
\(\frac{a−b}{b−a}=−1\)，\(a \ne b\)
表达式及其与 −1 的相反除法
我们将使用此属性来简化分子和分母中包含对立面的有理表达式。
简化：\(\frac{x−8}{8−x}\)。
解决方案
| \(\frac{x−8}{8−x}\)。 | |
| 认识到 x−8 和 8−x 是相反的 | −1 |
试试看\(\PageIndex{41}\)
简化：\(\frac{y−2}{2−y}\).
- Answer
-
−1
Try It \(\PageIndex{42}\)
简化：\(\frac{n−9}{9−n}\)。
- 回答
-
−1
请记住，简化有理表达式的第一步是将分子和分母完全分解。
简化：\(\frac{14−2x}{x^2−49}\)。
解决方案
 |
|
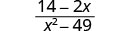| 系数分子和分母。 |  |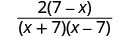
| 认识到 7−x 和 x−7 是相反的。 |  |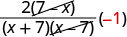
| 简化。 |  |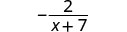
试试看\(\PageIndex{44}\)
简化：\(\frac{10−2y}{y^2−25}\).
- Answer
-
\(−\frac{2}{y+5}\)
Try It \(\PageIndex{45}\)
简化：\(\frac{3y−27}{81−y^2}\)。
- 回答
-
\(−\frac{3}{9+y}\)
简化：\(\frac{x^2−4x−32}{64−x^2}\)。
解决方案
 |
|
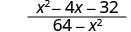| 系数分子和分母。 |  |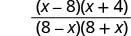
| 认识相反的因素。 |  |
| 简化。 |  |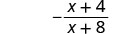
试试看\(\PageIndex{47}\)
简化：\(\frac{x^2−4x−5}{25−x^2}\).
- Answer
-
\(−\frac{x+1}{x+5}\)
Try It \(\PageIndex{48}\)
简化：\(\frac{x^2+x−2}{1−x^2}\)。
- 回答
-
\(−\frac{x+2}{x+1}\)
关键概念
- 确定未定义有理表达式的值
- 将分母设置为零。
- 如果可能，求解方程。
- 简化的有理表达
- 如果有理表达式的分子和分母中没有共同的因子，则认为有理表达式是简化的。
- 简化理性表达式
- 将分子和分母完全分解。
- 通过划分常见因素进行简化。
- 理性表达中的对立面
- a−b 的反面是 b−a
\(\frac{a−b}{b−a}=−1\)\(a \ne b\),\(b \ne 0\),\(a \ne b\)
- a−b 的反面是 b−a
练习成就完美
在以下练习中，确定有理表达式未定义的值。
- \(\frac{2x}{z}\)
- \(\frac{4p−1}{6p−5}\)
- \(\frac{n−3}{n^2+2n−8}\)
- 回答
-
- z=0
- \(p=\frac{5}{6}\)
- n=−4，n=2
- \(\frac{10m}{11n}\)
- \(\frac{6y+13}{4y−9}\)
- \(\frac{b−8}{b^2−36}\)
- \(\frac{4x^{2}y}{3y}\)
- \(\frac{3x−2}{2x+1}\)
- \(\frac{u−1}{u^2−3u−28}\)
- 回答
-
- y=0
- \(x=−\frac{1}{2}\)
- u=−4，u=7
- \(\frac{5pq^{2}}{9q}\)
- \(\frac{7a−4}{3a+5}\)
- \(\frac{1}{x^2−4}\)
在以下练习中，计算给定值的有理表达式。
\(\frac{2x}{x−1}\)
- x=0
- x=2
- x=−1
- 回答
-
- 0
- 4
- 1
\(\frac{4y−1}{5y−3}\)
- y=0
- y=2
- y=−1
\(\frac{2p+3}{p^2+1}\)
- p=0
- p=1
- p=−2
- 回答
-
- 3
- \(\frac{5}{2}\)
- \(−\frac{1}{5}\)
\(\frac{x+3}{2−3x}\)
- x=0
- x=1
- x=−2
\(\frac{y^2+5y+6}{y^2−1}\)
- y=0
- y=2
- y=−2
- 回答
-
- −6
- \(\frac{20}{3}\)
- 0
\(\frac{z^2+3z−10}{z^2−1}\)
- z=0
- z=2
- z=−2
\(\frac{a^2−4}{a^2+5a+4}\)
- a=0
- a=1
- a=−2
- 回答
-
- −1
- \(−\frac{3}{10}\)
- 0
\(\frac{b^2+2}{b^2−3b−4}\)
- b=0
- b=2
- b=−2
\(\frac{x^2+3xy+2y^2}{2x^{3}y}\)
- x=1，y=−1
- x=2，y=1
- x=−1，y=−2
- 回答
-
- 0
- \(\frac{3}{4}\)
- \(\frac{15}{4}\)
\(\frac{c^2+cd−2d^2}{cd^{3}}\)
- c=2，d=−1
- c=1，d=−1
- c=−1，d=2
\(\frac{m^2−4n^2}{5mn^3}\)
- m=2，n=1
- m=−1，n=−1
- m=3，n=2
- 回答
-
- 0
- \(−\frac{3}{5}\)
- \(−\frac{7}{20}\)
\(\frac{2s^{2}t}{s^2−9t^2}\)
- s=4，t=1
- s=−1，t=−1
- s=0，t=2
在以下练习中，进行简化。
\(−\frac{4}{52}\)
- 回答
-
\(−\frac{1}{13}\)
\(−\frac{44}{55}\)
\(\frac{56}{63}\)
- 回答
-
\(\frac{8}{9}\)
\(\frac{65}{104}\)
\(\frac{6ab^{2}}{12a^{2}b}\)
- 回答
-
\(\frac{b}{2ab}\)
\(\frac{15xy^{3}}{x^{3}y^{3}}\)
\(\frac{8m^{3}n}{12mn^2}\)
- 回答
-
\(\frac{2m^2}{3n}\)
\(\frac{36v^{3}w^2}{27vw^3}\)
\(\frac{3a+6}{4a+8}\)
- 回答
-
\(\frac{3}{4}\)
\(\frac{5b+5}{6b+6}\)
\(\frac{3c−9}{5c−15}\)
- 回答
-
\(\frac{3}{5}\)
\(\frac{4d+8}{9d+18}\)
\(\frac{7m+63}{5m+45}\)
- 回答
-
\(\frac{7}{5}\)
\(\frac{8n−96}{3n−36}\)
\(\frac{12p−240}{5p−100}\)
- 回答
-
\(\frac{12}{5}\)
\(\frac{6q+210}{5q+175}\)
\(\frac{a^2−a−12}{a^2−8a+16}\)
- 回答
-
\(\frac{a+3}{a−4}\)
\(\frac{x^2+4x−5}{x^2−2x+1}\)
\(\frac{y^2+3y−4}{y^2−6y+5}\)
- 回答
-
\(\frac{y+4}{y−5}\)
\(\frac{v^2+8v+15}{v^2−v−12}\)
\(\frac{x^2−25}{x^2+2x−15}\)
- 回答
-
\(\frac{x−5}{x−3}\)
\(\frac{a^2−4}{a^2+6a−16}\)
\(\frac{y^2−2y−3}{y^2−9}\)
- 回答
-
\(\frac{y+1}{y+3}\)
\(\frac{b^2+9b+18}{b^2−36}\)
\(\frac{y^3+y^2+y+1}{y^2+2y+1}\)
- 回答
-
\(\frac{y^2+1}{y+1}\)
\(\frac{p^3+3p^2+4p+12}{p^2+p−6}\)
\(\frac{x^3−2x^2−25x+50}{x^2−25}\)
- 回答
-
x−2
\(\frac{q^3+3q^2−4q−12}{q^2−4}\)
\(\frac{3a^2+15a}{6a^2+6a−36}\)
- 回答
-
\(\frac{a(a+5)}{2(a+3)(a−2)}\)
\(\frac{8b^2−32b}{2b^2−6b−80}\)
\(\frac{−5c^2−10c}{−10c^2+30c+100}\)
- 回答
-
\(\frac{c}{2(c−5)}\)
\(\frac{4d^2−24d}{2d^2−4d−48}\)
\(\frac{3m^2+30m+75}{4m^2−100}\)
- 回答
-
\(\frac{3(m+5)}{4(m−5)}\)
\(\frac{5n^2+30n+45}{2n^2−18}\)
\(\frac{5r^2+30r−35}{r^2−49}\)
- 回答
-
\(\frac{5(r−1)}{r+7}\)
\(\frac{3s^2+30s+24}{3s^2−48}\)
\(\frac{t^3−27}{t^2−9}\)
- 回答
-
\(\frac{t^2+3t+9}{t+3}\)
\(\frac{v^3−1}{v^2−1}\)
\(\frac{w^3+216}{w^2−36}\)
- 回答
-
\(\frac{w^2−6w+36}{w−6}\)
\(\frac{v^3+125}{v^2−25}\)
使用相反因子简化有理表达式
在以下练习中，简化每个有理表达式。
\(\frac{a−5}{5−a}\)
- 回答
-
−1
\(\frac{b−12}{12−b}\)
\(\frac{11−c}{c−11}\)
- 回答
-
−1
\(\frac{5−d}{d−5}\)
\(\frac{12−2x}{x^2−36}\)
- 回答
-
\(−\frac{2}{x+6}\)
\(\frac{20−5y}{y^2−16}\)
\(\frac{4v−32}{64−v^2}\)
- 回答
-
\(−\frac{4}{8+v}\)
\(\frac{7w−21}{9−w^2}\)
\(\frac{y^2−11y+24}{9−y^2}\)
- 回答
-
\(−\frac{y−8}{3+y}\)
\(\frac{z^2−9z+20}{16−z^2}\)
\(\frac{a^2−5a−36}{81−a^2}\)
- 回答
-
\(−\frac{a+4}{9+a}\)
\(\frac{b^2+b−42}{36−b^2}\)
日常数学
税率对于2015纳税年度，收入在37,450美元至90,750美元之间的单身人士所欠的税额可以通过计算公式0.25x−4206.25得出，其中 x 是收入。 通过评估公式可以找到该收入的平均税率\(\frac{0.25x−4206.25}{x}\)。 收入为50,000美元的单身人士的平均税率是多少？
- 回答
-
16.5％
工作通过评估公式可以得出两个人在一起工作时执行相同任务所花费的时间长度\(\frac{xy}{x+y}\)。 如果汤姆能在 x=45 分钟内画出书房，而他的兄弟 Bobby 能在 y=60 分钟内画出来，那么如果他们一起工作需要多少分钟？
写作练习
解释如何找到未定义有理表达式\(\frac{x^2−x−20}{x^2−4}\)的 x 的值。
解释你为简化理性表达而采取的所有步骤\(\frac{p^2+4p−21}{9−p^2}\)。
自检
ⓐ 完成练习后，使用这份清单来评估你对本节目标的掌握程度。
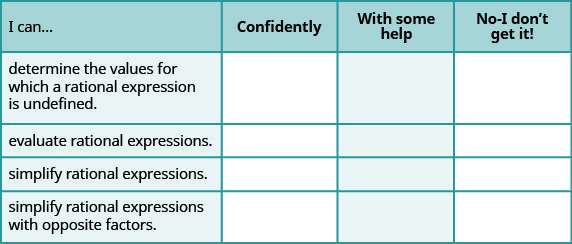
ⓑ 如果你的大部分支票是：
... 自信地。 恭喜！ 您已经在本节中实现了目标！ 反思一下你使用的学习技能，这样你就可以继续使用它们。 为了确信自己有能力做这些事情，你做了什么？ 具体一点！
... 在一些帮助下。 必须尽快解决这个问题，因为你不掌握的话题会成为你通往成功之路的坑洼。 数学是顺序的——每个主题都建立在先前工作的基础上。 在继续前进之前，请务必确保自己有坚实的基础。 你能向谁寻求帮助？ 你的同学和老师都是很好的资源。 校园里有没有可以提供数学导师的地方？ 你的学习技能可以提高吗？
... 不-我不明白！ 这很关键，你一定不能忽视它。 你需要立即获得帮助，否则你很快就会不知所措。 尽快与您的教师见面，讨论您的情况。 你可以一起制定一个计划，为你提供所需的帮助。
词汇表
- 理性表达
- 有理表达式是这种形式的表达式\(\frac{p}{q}\)，其中 p 和 q 是多项式，\(q \ne 0\).