第 8 章复习练习
- Page ID
- 204812
章节复习练习
简化有理表达式
确定未定义有理表达式的值
在以下练习中,确定有理表达式未定义的值。
\(\dfrac{2a+1}{3a−2}\)
- 回答
-
\(a \ne \dfrac{2}{3}\)
\(\dfrac{b−3}{b^2−16}\)
\(\dfrac{3xy^2}{5y}\)
- 回答
-
\(y \ne 0\)
\(\dfrac{u−3}{u^2−u−30}\)
评估有理表达式
在以下练习中,计算给定值的有理表达式。
\(\dfrac{4p−1}{p^2+5}\)什么时候\(p=−1\)
- 回答
-
\(−\dfrac{5}{6}\)
\(\dfrac{q^2−5}{q+3}\)什么时候\(q=7\)
\(\dfrac{y^2−8}{y^2−y−2}\)什么时候\(y=1\)
- 回答
-
\(\dfrac{7}{2}\)
\(\dfrac{z^2+2}{4z−z^2}\)什么时候\(z=3\)
在以下练习中,进行简化。
\(\dfrac{10}{24}\)
- 回答
-
\(\dfrac{5}{12}\)
\(\dfrac{8m^4}{16mn^3}\)
\(\dfrac{14a−14}{a−1}\)
- 回答
-
\(14\)
\(\dfrac{b^2+7b+12}{b^2+8b+16}\)
使用相反因子简化有理表达式
在以下练习中,进行简化。
\(\dfrac{c^2−c−2}{4−c^2}\)
- 回答
-
\(-\dfrac{c+1}{c+2}\)
\(\dfrac{d−16}{16−d}\)
\(\dfrac{7v−35}{25−v^2}\)
- 回答
-
\(−\dfrac{7}{5+v}\)
\(\dfrac{w^2−3w−28}{49−w^2}\)
有理表达式的乘法和除法
乘以有理表达式
在以下练习中,乘以。
\(\dfrac{3}{8}·\dfrac{2}{15}\)
- 回答
-
\(\dfrac{1}{20}\)
\(\dfrac{2xy^2}{8y^3}·\dfrac{16y}{24x}\)
\(\dfrac{3a^2+21a}{a^2+6a−7}·\dfrac{a−1}{ab}\)
- 回答
-
\(\dfrac{3}{b}\)
\(\dfrac{5z^2}{5z^2+40z+35}·\dfrac{z^2−1}{3z}\)
划分有理表达式
在以下练习中,除以。
\(\dfrac{t^2−4t-12}{t^2+8t+12}÷\dfrac{t^2−36}{6t}\)
- 回答
-
\(\dfrac{6t}{(t+6)^2}\)
\(\dfrac{r^2−16}{4}÷\dfrac{r^3−64}{2r^2−8r+32}\)
\(\dfrac{11+w}{w−9}÷\dfrac{121−w^2}{9−w}\)
- 回答
-
\(\dfrac{1}{11+w}\)
\(\dfrac{3y^2−12y−63}{4y+3}÷(6y^2−42y)\)
\(\dfrac{\dfrac{c^2−64}{3c^2+26c+16}}{\dfrac{c^2−4c−32}{15c+10}}\)
- 回答
-
\(5c+4\)
\(\dfrac{8m^2−8m}{m−4}·\dfrac{m^2+2m−24}{m^2+7m+10}÷\dfrac{2m^2−6m}{m+5}\)
用公分母加减有理表达式
添加带有公分母的有理表达式
在以下练习中,添加。
\(\dfrac{3}{5}+\dfrac{2}{5}\)
- 回答
-
\(1\)
\(\dfrac{4a^2}{2a−1}−\dfrac{1}{2a−1}\)
\(\dfrac{p^2+10p}{p+5}+\dfrac{25}{p+5}\)
- 回答
-
\(p+5\)
\(\dfrac{3x}{x−1}+\dfrac{2}{x−1}\)
用公分母减去有理表达式
在以下练习中,减去。
\(\dfrac{d^2}{d+4}−\dfrac{3d+28}{d+4}\)
- 回答
-
\(d-7\)
\(\dfrac{z^2}{z+10}−\dfrac{100}{z+10}\)
\(\dfrac{4q^2−q+3}{q^2+6q+5}−\dfrac{3q^2+q+6}{q^2+6q+5}\)
- 回答
-
\(\dfrac{q−3}{q+5}\)
\(\dfrac{5t+4t+3}{t^2−25}−\dfrac{4t^2−8t−32}{t^2−25}\)
在以下练习中,加减法。
\(\dfrac{18w}{6w−1}+\dfrac{3w−2}{1−6w}\)
- 回答
-
\(\dfrac{15w+2}{6w−1}\)
\(\dfrac{a^2+3a}{a^2−4}−\dfrac{3a−8}{4−a^2}\)
\(\dfrac{2b^2+3b−15}{b^2−49}−\dfrac{b^2+16b−1}{49−b^2}\)
- 回答
-
\(\dfrac{3b−2}{b+7}\)
\(\dfrac{8y^2−10y+7}{2y−5}+\dfrac{2y^2+7y+2}{5−2y}\)
使用不同分母加减有理表达式
找出有理表达式的最小公分母
在以下练习中,找到 LCD。
\(\dfrac{4}{m^2−3m−10},\quad\dfrac{2m}{m^2−m−20}\)
- 回答
-
\((m+2)(m−5)(m+4)\)
\(\dfrac{6}{n^2−4},\quad\dfrac{2n}{n^2−4n+4}\)
\(\dfrac{5}{3p^2+17p−6},\quad\dfrac{2m}{3p^2−23p−8}\)
- 回答
-
\((3p+1)(p+6)(p+8)\)
在以下练习中,使用给定的分母重写为等效有理表达式。
用分母重写为等效有理表达式\((m+2)(m−5)(m+4)\)
\(\dfrac{4}{m^2−3m−10},\quad\dfrac{2m}{m^2−m−20}\)。
用分母重写为等效有理表达式\((n−2)(n−2)(n+2)\)
\(\dfrac{6}{n^2−4n+4},\quad\dfrac{2n}{n^2−4}\)。
- 回答
-
\(\dfrac{6n+12}{(n−2)(n−2)(n+2)},\quad\dfrac{2n^2−4n}{(n−2)(n−2)(n+2)}\)
用分母重写为等效有理表达式\((3p+1)(p+6)(p+8)\)
\(\dfrac{5}{3p^2+19p+6},\quad\dfrac{7p}{3p^2+25p+8}\)
在以下练习中,添加。
\(\dfrac{2}{3}+\dfrac{3}{5}\)
- 回答
-
\(\dfrac{19}{15}\)
\(\dfrac{7}{5a}+\dfrac{3}{2b}\)
\(\dfrac{2}{c−2}+\dfrac{9}{c+3}\)
- 回答
-
\(\dfrac{11c−12}{(c−2)(c+3)}\)
\(\dfrac{3d}{d^2−9}+\dfrac{5}{d^2+6d+9}\)
\(\dfrac{2x}{x^2+10x+24}+\dfrac{3x}{x^2+8x+16}\)
- 回答
-
\(\dfrac{5x^2+26x}{(x+4)(x+4)(x+6)}\)
\(\dfrac{5q}{p^{2}q−p^2}+\dfrac{4q}{q^2−1}\)
在以下练习中,减去和相加。
\(\dfrac{3v}{v+2}−\dfrac{v+2}{v+8}\)
- 回答
-
\(\dfrac{2(v^2+10v−2)}{(v+2)(v+8)}\)
\(\dfrac{−3w−15}{w^2+w−20}−\dfrac{w+2}{4−w}\)
\(\dfrac{7m+3}{m+2}−5\)
- 回答
-
\(\dfrac{2m−7}{m+2}\)
\(\dfrac{n}{n+3}+\dfrac{2}{n−3}−\dfrac{n−9}{n^2−9}\)
\(\dfrac{8d}{d^2−64}−\dfrac{4}{d+8}\)
- 回答
-
\(4d−8\)
\(\dfrac{5}{12x^{2}y}+\dfrac{7}{20xy^3}\)
简化复杂的有理表达式
通过将复杂的有理表达式写成 Division 来简化它
在以下练习中,进行简化。
\(\dfrac{\dfrac{5a}{a+2}}{\dfrac{10a^2}{a^2−4}}\)
- 回答
-
\(\dfrac{a−2}{2a}\)
\(\dfrac{\dfrac{2}{5}+\dfrac{5}{6}}{\dfrac{1}{3}+\dfrac{1}{4}}\)
\(\dfrac{x−\dfrac{3x}{x+5}}{\dfrac{1}{x+5}+\dfrac{1}{x−5}}\)
- 回答
-
\(\dfrac{(x−8)(x−5)}{2}\)
\(\dfrac{\dfrac{2}{m}+\dfrac{m}{n}}{\dfrac{n}{m}−\dfrac{1}{n}}\)
在以下练习中,进行简化。
\(\dfrac{6+\dfrac{2}{q−4}}{\dfrac{5}{q}+4}\)
- 回答
-
\(\dfrac{(q−2)(q+4)}{5(q−4)}\)
\(\dfrac{\dfrac{3}{a^2}−\dfrac{1}{b}}{\dfrac{1}{a}+\dfrac{1}{b^2}}\)
\(\dfrac{\dfrac{2}{z^2−49}+\dfrac{1}{z+7}}{\dfrac{9}{z+7}+\dfrac{12}{z−7}}\)
- 回答
-
\(\dfrac{z−5}{21z+21}\)
\(\dfrac{\dfrac{3}{y^2−4y−32}}{\dfrac{2}{y−8}+\dfrac{1}{y+4}}\)
求解有理方程
求解有理方程
在以下练习中,求解。
\(\dfrac{1}{2}+\dfrac{2}{3}=\dfrac{1}{x}\)
- 回答
-
\(\dfrac{6}{7}\)
\(1−\dfrac{2}{m}=\dfrac{8}{m^2}\)
\(\dfrac{1}{b−2}+\dfrac{1}{b+2}=\dfrac{3}{b^2−4}\)
- 回答
-
\(\dfrac{3}{2}\)
\(\dfrac{3}{q+8}−\dfrac{2}{q−2}=1\)
\(\dfrac{v−15}{v^2−9v+18}=\dfrac{4}{v−3}+\dfrac{2}{v−6}\)
- 回答
-
没有解决办法
\(\dfrac{z}{12}+\dfrac{z+3}{3z}=\dfrac{1}{z}\)
求解特定变量的有理方程
在以下练习中,求解指定变量。
\(\dfrac{V}{l}=hw\)为了\(l\)
- 回答
-
\(l=\dfrac{V}{hw}\)
\(\dfrac{1}{x}−\dfrac{2}{y}=5\)为了\(y\)
\(x=\dfrac{y+5}{z−7}\)为了\(z\)
- 回答
-
\(z=\dfrac{y+5+7x}{x}\)
\(P=\dfrac{k}{V}\)为了\(V\)
求解比例和相似图应用相似度
求解比例
在以下练习中,求解。
\(\dfrac{x}{4}=\dfrac{3}{5}\)
- 回答
-
\(\dfrac{12}{5}\)
\(\dfrac{3}{y}=\dfrac{9}{5}\)
\(\dfrac{s}{s+20}=\dfrac{3}{7}\)
- 回答
-
\(15\)
\(\dfrac{t−3}{5}=\dfrac{t+2}{9}\)
在以下练习中,使用比例求解。
Rachael 吃了一\(21\)盎司\(739\)含有卡路里的草莓奶昔。 一\(32\)盎司奶昔中有多少卡路里?
- 回答
-
\(1161\)卡路里
Leo 在圣诞节假期去了墨西哥,将\($525\)美元兑换成了墨西哥比索。 当时,美元的汇率等于\(16.25\)墨西哥比索。\($1\) 他这次旅行得到了多少墨西哥比索?
在以下练习中,求解。
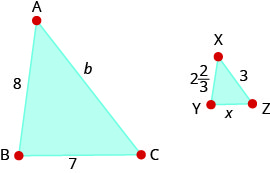
\(∆ABC\)类似于\(∆XYZ\)。 图中给出了每个三角形两边的长度。 找出第三边的长度。
- 回答
-
\(b=9\);\(x=2\dfrac{1}{3}\)
在欧洲地图上,巴黎、罗马和维也纳形成一个三角形,其边如下图所示。 如果从罗马到维也纳的实际距离是\(700\)英里,请找到距离
- a. 从巴黎到罗马
- b. 从巴黎到维也纳
托尼身高一\(5.75\)英尺。 一天下午晚些时候,他的影子长一\(8\)英尺。 同时,附近一棵树的阴影长达几\(32\)英尺。 找出树的高度。
- 回答
-
\(23\)英尺
佛罗里达州彭萨科拉的一座灯塔的高度是\(150\)英尺。 站在雕像旁边,一\(5.5\)英尺高的娜塔莉投下了\(1.1\)脚影,灯塔的阴影会持续多久?
解决均匀运动和工作应用问题
求解均匀运动应用程序
在以下练习中,求解。
丽莎在去探望父母后开车5小时回家时,遇到了恶劣的天气。 天气好的时候她可以行驶\(176\)数英里, 但是后来慢了\(10\)英里每小时, 在恶劣的天气下行驶了\(81\)几英里. 天气不好的时候她开了多快?
- 回答
-
45 英里每小时
马克乘坐的飞机可以以英里\(20\) /小时的顺风飞行\(490\)数英里,同时它可以在英里/小时的顺风下飞行\(350\)数\(20\)英里. 飞机的速度是多少?
约翰骑自行车的\(8\)速度比卢克骑自行车的速度更快. 卢克比约翰长\(3\)几个小时才能骑行\(48\)里程。 约翰能骑多快自行车?
- 回答
-
\(16\)mph
马克正在为铁人三项训练。 他在总共\(3\)几个小时内跑\(8\)了\(32\)几公里并骑了几公里. 他的跑步速度比骑自行车的速度低每小时\(8\)千米。 他的跑步速度是多少?
在以下练习中,求解。
杰瑞可以在一\(1\)小时内构筑一个房间,而杰克则需要\(4\)几个小时。 他们能一起搭建一个房间多久?
- 回答
-
\(\dfrac{4}{5}\)小时
丽莎需要\(3\)几个小时来修剪草坪,而她的堂兄 Barb 则需要\(2\)几个小时。 他们一起工作需要多长时间?
杰弗里可以在\(6\)几天之内粉刷房子,但如果他有帮手,他可以在\(4\)几天之内完成。 帮手独自粉刷房子要花多长时间?
- 回答
-
\(12\)天
Sue 和 Deb 一起写了一本花了他们\(90\)几天的书。 如果 Sue 一个人工作,那将花费她\(120\)几天时间。 Deb 独自写这本书要花多长时间?
使用直接变异和逆变异
解决直接变异问题
在以下练习中,求解。
它直接\(y\)变化\(x\),比如,何时\(y=9\)和\(x=3\),找出\(x\)时间\(y=21\)。
- 回答
-
\(7\)
它直接\(y\)变化\(x\),比如,何时\(y=20\)和\(x=2\),找出\(y\)时间\(x=4\)。
它\(m\)与\(n\)、when\(m=4\) 和\(n=6\) fin\(m\) d when 的平方成反比\(n=2\)。
- 回答
-
\(36\)
凡妮莎正在旅行去见她的未婚夫。 距离,\(d\),直接随速度而变化,\(v\),她开车。 如果她以英里/小时的\(60\)速度行驶\(258\)数英里, 她会以英里/小时的\(70\)速度行驶多远?
如果披萨的成本直接随其直径而变化,如果一个\(8\) “直径” 的披萨的价格是多少\($12\),那么\(6\) “直径” 的披萨要花多少钱?
- 回答
-
\($9\)
停下汽车的距离直接随其速度的平方而变化。 阻止汽车以\(200\)英里/小时的速度行驶需要\(50\)英尺. 阻止一辆汽车以英里/小时的速度行驶需要多少\(60\)英尺?
在以下练习中,求解。
音乐筹款活动的门票数量与门票价格成反比。 如果玛德琳有足够的钱购买\(12\)门票\($6\),那么如果价格上涨到了,玛德琳能买多少张票\($8\)?
- 回答
-
\(97\)门票
在弦乐器上,弦的长度与其振动频率成反比。 如果小提琴上的\(11\)-inch 弦具有每秒\(360\)循环的频率,那么\(12\)-inch 琴弦的频率是多少?
练习测试
在以下练习中,进行简化。
\(\dfrac{3a^{2}b}{6ab^2}\)
- 回答
-
\(\dfrac{a}{2b}\)
\(\dfrac{5b−25}{b^2−25}\)
在以下练习中,执行指定的操作并进行简化。
\(\dfrac{4x}{x+2}·\dfrac{x^2+5x+6}{12x^2}\)
- 回答
-
\(\dfrac{x+3}{3x}\)
\(\dfrac{5y}{4y−8}·\dfrac{y^2−4}{10}\)
\(\dfrac{4p}{q}+\dfrac{5}{p}\)
- 回答
-
\(\dfrac{4+5q}{pq}\)
\(\dfrac{1}{z−9}−\dfrac{3}{z+9}\)
\(\dfrac{\dfrac{2}{3}+\dfrac{3}{5}}{\dfrac{2}{5}}\)
- 回答
-
\(\dfrac{19}{16}\)
\(\dfrac{\dfrac{1}{m}−\dfrac{1}{n}}{\dfrac{1}{n}+\dfrac{1}{m}}\)
在以下练习中,求解每个方程。
\(\dfrac{1}{2}+\dfrac{2}{7}=\dfrac{1}{x}\)
- 回答
-
\(x = \dfrac{14}{11}\)
\(\dfrac{5}{y−6}=\dfrac{3}{y+6}\)
\(\dfrac{1}{z−5}+\dfrac{1}{z+5}=\dfrac{1}{z^2−25}\)
- 回答
-
\(z = \dfrac{1}{2}\)
\(\dfrac{t}{4}=\dfrac{3}{5}\)
\(\dfrac{2}{r−2}=\dfrac{3}{r−1}\)
- 回答
-
\(r = 4\)
在以下练习中,求解。
它直接\(y\)随时间\(x\)而变化\(x=5\)\(y=30\),找出\(x\)时间\(y=42\)。
如果\(y\)与时间成反比\(x\)\(y=20\),\(x=6\)则找出\(y\)时间\(x=2\)。
- 回答
-
\(y=60\)
如果与\(y\) when\(x\) 和\(x=3\) when 的平方成反比\(y=9\),请找出\(y\)时间\(x=4\)。
狗的推荐红霉素剂量是狗每重一磅的\(5\)毫克。 如果黛西体重一\(25\)磅,她的兽医应该开多少毫克的红霉素?
- 回答
-
\(125\)毫克
周日下午,朱莉娅花了\(4\)几个小时在健身房锻炼身体。 她在跑步机上跑了\(10\)几英里然后骑了\(20\)几英里。 她的骑行\(5\)速度比跑步机上的跑步速度快mph. 她的跑步速度是多少?
库尔特可以在风中骑自行车行驶数\(30\)英里,时间与逆风行驶数\(21\)英里的时间相同。 如果风速是\(6\)英里每小时,那么库尔特骑自行车的速度是多少?
- 回答
-
\(14\)mph
阿曼达(Amanda\(8\))使用一条路线慢跑到公园数英里,然后通过一条\(14\)-英里路线返回. 回程比她慢跑到公园花费的时间要长\(1\)一个小时。 找出她的慢跑速率
经验丰富的洗窗机可以在\(2\)数小时内清洗迈克家的所有窗户,而新学员可以在\(7\)数小时内清洗所有窗户。 他们一起工作需要多长时间?
- 回答
-
\(1\frac{5}{9}\)小时
Josh 可以在\(8\)几个小时内拆分一卡车的日志,但是和他父亲一起工作他们可以在\(3\)几个小时内完成。 Josh 的爸爸独自工作要花多长时间才能拆分日志?
泰勒为汽油支付的价格与他购买的加仑数量直接不同。 如果\(24\)加仑花了他钱\($59.76\),\(30\)加仑要花多少钱?
- 回答
-
\($74.70\)
容器中气体的体积与气体上的压力成反比。 如果氮气容器的体积为\(29.5\)升,\(2000\)psi,那么如果储罐的额定值为\(14.7\) psi,则容量是多少? 四舍五入到最接近的整数。
代顿、哥伦布和辛辛那提等城市在俄亥俄州南部形成一个三角形,如下图所示,这给出了这些城市之间的地图距离(以英寸为单位)。
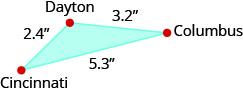
从代顿到辛辛那提的实际距离为\(48\)英里. 代顿和哥伦布之间的实际距离是多少?
- 回答
-
\(64\)英里