6.4: 特殊产品
- Page ID
- 204999
在本节结束时,您将能够:
- 使用二项式方块图案对二项式进行平方
- 使用共轭物乘积图案将共轭物相乘
- 识别并使用相应的特殊产品图案
使用二项式方块图案对二项式进行平方
数学家喜欢寻找能使他们的工作更轻松的模式。 这方面的一个很好的例子是二项式的平方。 虽然你总是可以通过写两次二项式并使用最后一节的方法来获得乘积,但如果你学会使用模式,那么要做的工作就少了。
\[\begin{array}{ll}{\text { Let's start by looking at }(x+9)^{2} \text { . }}& \\ {\text { What does this mean? }} &{(x+9)^{2}} \\ {\text { It means to multiply }(x+9) \text { by itself. }} & {(x+9)(x+9)}\\ {\text { Then, using FOIL, we get: }} & {x^{2}+9 x+9 x+81}\\ {\text { Combining like terms gives: }} &{x^{2}+18 x+81} \\ \\ {\text { Here's another one: }} & {(y-7)^{2}} \\ {\text { Multiply }(y-7) \text { by itself. }} & {(y-7)(y-7)} \\ {\text { Using FOIL, we get: }} & {y^{2}-7 y-7 y+49} \\ {\text { And combining like terms: }} & {y^{2}-14 y+49} \\ \\ {\text { And one more: }} & {(2 x+3)^{2}} \\ {\text { Multiply. }} & {(2 x+3)(2 x+3)} \\ {\text { Use FOIL: }} & {\text { 4x }+6 x+6 x+9} \\ {\text { Combine like terms. }} & {4 x^{2}+12 x+9}\end{array} \nonumber\]
看看这些结果。 你看到任何图案了吗?
那么术语的数量呢? 在每个例子中,我们求一个二项式的平方,结果是三项式。
\[(a+b)^{2}=\underline{\qquad}+\underline{\qquad}+\underline{\qquad}\nonumber \]
现在看每个结果中的第一个术语。 它来自哪里?
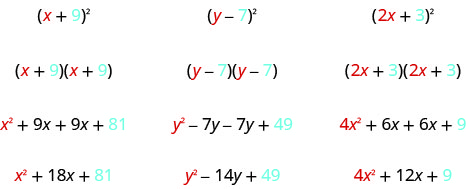
第一个项是每个二项式的第一个项的乘积。 由于二项式是相同的,它只是第一个项的平方!
\[(a+b)^{2}=a^{2}+\underline{\qquad}+\underline{\qquad}\nonumber \]
要获得乘积的第一个项,请对第一个项进行平方。
最后一个学期来自哪里? 看看例子并找到模式。
最后一个项是最后一个项的乘积,即最后一个项的平方。
\[(a+b)^{2}=\underline{\qquad}+\underline{\qquad}+b^{2}\nonumber \]
要获得产品的最后一个项,请将最后一个项相乘。
最后,看看中间学期。 请注意,它源于添加 “外部” 和 “内部” 术语——两者都是一样的! 因此,中间项是二项式两个项乘积的两倍。
\[(a+b)^{2}=\underline{\qquad}+2ab+\underline{\qquad}\nonumber \]
\[(a+b)^{2}=\underline{\qquad}-2ab+\underline{\qquad}\nonumber \]
要得出产品的中间项,请将这些项相乘并将其乘积加倍。
把它们放在一起:
如果\(a\)和\(b\)是实数,则二项式方形图案为
\[\underbrace{(a+b)^{2}}_{(\text{binomial})^2} = \underbrace{a^{2}}_{(\text{first term})^2} + \underbrace{2 a b}_{2 \times (\text{product of terms})} + \underbrace{a^{2}}_{(\text{last term})^2} \nonumber\]
将其应用于两种二项式类型:
\[\begin{align*} (a+b)^{2} &= a^{2}+2 a b+b^{2} \\[4pt] (a-b)^{2} &=a^{2}- 2 a b + b^{2} \end{align*}\]
要求二项式的平方:
- 用第一个术语求平方
- 与最后一个学期相提并论
- 将他们的产品翻倍
数字示例有助于验证模式。
\(\begin{array}{ll} & {(10+4)^{2}} \\{\text { Square the first term. }}& {10^{2}+\underline{\qquad}+\underline{\qquad}} \\ {\text { Square the last term. }} & {10^{2}+\underline{\qquad}+\frac{1}{4^{2}}} \\ {\text { Double their product. }} & {10^{2}+2 \cdot 10 \cdot 4+4^{2}} \\ {\text { Simplify. }} & {100+80+16} \\ {\text { Simplify. }} & {196}\end{array}\)
要乘以\((10+4)^2\)通常需要遵循操作顺序。
\[\begin{array}{c}{(10+4)^{2}} \\ {(14)^{2}} \\ {196}\end{array}\nonumber \]
图案起作用了!
\(\text { Multiply: }(x+5)^{2}\)
解决方案:
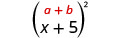 |
|
| 用第一个术语求平方。 |  |
| 将最后一个术语平方。 |  |
| 将产品加倍。 |  |
| 简化。 | \(x^{2}+10 x+25\) |
乘以:\((x+9)^{2}\)
- 回答
-
\(x^{2}+18 x+81\)
乘以:\((y+11)^{2}\)
- 回答
-
\(y^{2}+22 y+121\)
乘以:\((y-3)^{2}\)
解决方案:
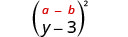 |
|
| 用第一个术语求平方。 |  |
| 将最后一个术语平方。 |  |
| 将产品加倍。 | 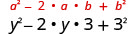 |
| 简化。 | \(y^{2}-6 y+9\) |
乘以:\((x-9)^{2}\)
- 回答
-
\(x^{2}-18 x+81\)
乘以:\((p-13)^{2}\)
- 回答
-
\(p^{2}-26 p+169\)
乘以:\((4 x+6)^{2}\)
解决方案:
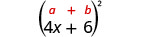 |
|
| 使用图案。 | 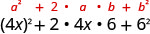 |
| 简化。 | \(16 x^{2}+48 x+36\) |
乘以:\((6 x+3)^{2}\)
- 回答
-
\(36 x^{2}+36 x+9\)
乘以:\((4 x+9)^{2}\)
- 回答
-
\(16 x^{2}+72 x+81\)
乘以:\((2 x-3 y)^{2}\)
解决方案:
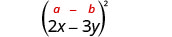 |
|
| 使用图案。 | 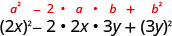 |
| 简化。 | \(4 x^{2}-12 x y+9 y^{2}\) |
乘以:\((2 c-d)^{2}\)
- 回答
-
\(4 c^{2}-4 c d+d^{2}\)
乘以:\((4 x-5 y)^{2}\)
- 回答
-
\(16 x^{2}-40 x y+25 y^{2}\)
乘以:\(\left(4 u^{3}+1\right)^{2}\)
解决方案:
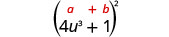 |
|
| 使用图案。 | 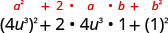 |
| 简化。 | \(16 u^{6}+8 u^{3}+1\) |
乘以:\(\left(2 x^{2}+1\right)^{2}\)
- 回答
-
\(4 x^{4}+4 x^{2}+1\)
乘以:\(\left(3 y^{3}+2\right)^{2}\)
- 回答
-
\(9 y^{6}+12 y^{3}+4\)
使用共轭物乘积图案乘以共轭物
我们刚刚看到了一种二项式求平方的模式,我们可以用它来简化一些二项式的乘法。 同样,二项式的另一种乘积也有一种模式。 但是在我们开始之前,我们需要介绍一些词汇。
你对这两对二项式有什么看法?
\[(x-9)(x+9) \qquad(y-8)(y+8)\qquad (2x-5)(2x+5) \nonumber\]
看看每对中每个二项式的第一个项。
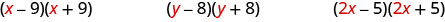
请注意,每对中的第一个项是相同的。
看看每对中每个二项式的最后一个项。
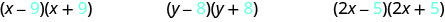
请注意,每对中的最后一个术语是相同的。
注意每对都有一个总和和和和和和一个差异。
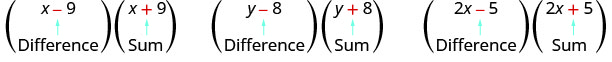
一对二项式的第一个项和最后一个项相同,但一个是总和,一个是差值,它们有一个特殊的名称。 它被称为共轭对,形式为 (a−b)、(a+b)。
共轭对是两个形式的二项式
\[(a-b),(a+b)\nonumber \]
两对二项式的第一个项和最后一个项相同,但是一个二项式是总和,另一个是差异。
找到共轭物的乘积有很好的模式。 当然,你可以简单地用 FOIL 来获得产品,但是使用这种模式可以让你的工作更轻松。
让我们使用 FOIL 乘以一些共轭对来寻找模式。
\[\begin{array}{cc}{(x-9)(x+9)} & {(y-8)(y+8)} & (2x-5)(2x+5)\\ {x^{2}+9 x-9 x-81} & {y^{2}+8 y-8 y-64} & {4 x^{2}+10 x-10 x-25} \\ {x^{2}-81} & {y^{2}-64} & {4 x^{2}-25}\end{array}\nonumber \]
每个第一个项都是二项式第一个项的乘积,由于它们是相同的,因此它是第一个项的平方。
\[\begin{array}{c}{(a+b)(a-b)=a^{2}-}\underline{\qquad} \\ {\text { To get the}\textbf{ first term, square the first term. }}\end{array}\nonumber \]
最后一个术语来自于最后一个项的乘积,即最后一个学期的平方。
\[\begin{array}{c}{(a+b)(a-b)=a^{2}-b^{2}} \\ {\text { To get the}\textbf{ last term, square the last term. }}\end{array}\nonumber \]
您对这些产品有什么看法?
两个二项式的乘积也是二项式! 由FOIL产生的大多数产品都是三项式的。
为什么没有中间学期? 请注意,在每种情况下,你从 FOIL 中得到的两个中间项组合为 0,这是一加一减的结果。
共轭物的乘积总是这样的\(a^2-b^2\)。 这称为平方差。
这导致了以下模式:
如果\(a\)和\(b\)是实数,

该乘积称为平方差。
要乘以共轭,请将第一个项求平方,将最后一个项求平方,然后将乘积写为平方差。
让我们用一个数字示例来测试这个模式。
\(\begin{array}{ll} & (10-2)(10+2)\\ {\text { It is the product of conjugates, so the result will be the }} \\ {\text { difference of two squares. }} & \underline{\qquad} - \underline{\qquad}\\ {\text { Square the first term. }}& 10^2 - \underline{\qquad} \\ {\text { Square the last term. }} & 10^2 - 2^2\\ {\text { Simplify. }} & 100 -4\\ {\text { Simplify. }} & 96\\ {\text { What do you get using the Order of Operations? }} \\ \\ & (10-2)(10+2) \\ & (8)(12) \\ & 96 \end{array}\)
注意,结果是一样的!
乘以:\((x-8)(x+8)\)
解决方案:
首先,将其视为共轭物的产物。 二项式具有相同的第一项和最后一项相同,一个二项式是总和,另一个是差值。
| 它符合图案。 | 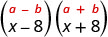 |
| 取第一个项 x 的平方。 | 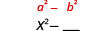 |
| 取最后一个学期的平方,8。 | 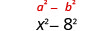 |
| 该乘积是平方差。 | 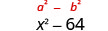 |
乘以:\((x-5)(x+5)\)
- 回答
-
\(x^{2}-25\)
乘以:\((w-3)(w+3)\)
- 回答
-
\(w^{2}-9\)
乘以:\((2 x+5)(2 x-5)\)
解决方案:
二项式是共轭物吗?
| 它是偶联物的产物。 | 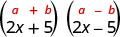 |
| 将第一个项平方,2 x。 | 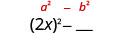 |
| 取最后一个学期的平方,5。 | 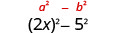 |
| 简化。 该乘积是平方差。 | 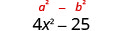 |
乘以:\((6 x+5)(6 x-5)\)
- 回答
-
\(36 x^{2}-25\)
乘以:\((2 x+7)(2 x-7)\)
- 回答
-
\(4 x^{2}-49\)
下一个示例中的二项式可能会向后看 — 变量在第二个项中。 但是这两个二项式仍然是共轭物,所以我们使用相同的模式将它们相乘。
查找产品:\((3+5 x)(3-5 x)\)
解决方案:
| 它是偶联物的产物。 | 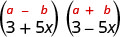 |
| 使用图案。 | 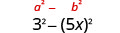 |
| 简化。 | \(9-25 x^{2}\) |
乘以:\((7+4 x)(7-4 x)\)
- 回答
-
\(49-16 x^{2}\)
乘以:\((9-2 y)(9+2 y)\)
- 回答
-
\(81-4 y^{2}\)
现在我们将乘以具有两个变量的共轭。
查找产品:\((5 m-9 n)(5 m+9 n)\)
解决方案:
| 这符合图案。 | 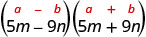 |
| 使用图案。 | 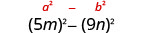 |
| 简化。 | \(25 m^{2}-81 n^{2}\) |
查找产品:\((4 p-7 q)(4 p+7 q)\)
- 回答
-
\(16 p^{2}-49 q^{2}\)
查找产品:\((3 x-y)(3 x+y)\)
- 回答
-
\(9 x^{2}-y^{2}\)
查找产品:\((c d-8)(c d+8)\)
解决方案:
| 这符合图案。 | 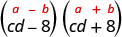 |
| 使用图案。 | 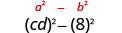 |
| 简化。 | \(c^{2} d^{2}-64\) |
查找产品:\((x y-6)(x y+6)\)
- 回答
-
\(x^{2} y^{2}-36\)
查找产品:\((a b-9)(a b+9)\)
- 回答
-
\(a^{2} b^{2}-81\)
查找产品:\(\left(6 u^{2}-11 v^{5}\right)\left(6 u^{2}+11 v^{5}\right)\)
解决方案:
| 这符合图案。 | 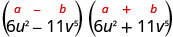 |
| 使用图案。 | 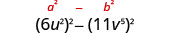 |
| 简化。 | \(36 u^{4}-121 v^{10}\) |
查找产品:\(\left(3 x^{2}-4 y^{3}\right)\left(3 x^{2}+4 y^{3}\right)\)
- 回答
-
\(9 x^{4}-16 y^{6}\)
查找产品:\(\left(2 m^{2}-5 n^{3}\right)\left(2 m^{2}+5 n^{3}\right)\)
- 回答
-
\(4 m^{4}-25 n^{6}\)
识别并使用相应的特殊产品图案
我们刚刚为二项式方块和共轭物乘积开发了特殊的乘积模式。 这些产品看起来很相似,因此重要的是要识别何时适合使用每种模式,并注意它们的不同之处。 一起看这两种模式,注意它们的相似之处和不同之处。
\(\begin{array}{ll }{\textbf { Binomial Squares }}&{\textbf { Product of Conjugates }} \\ {(a+b)^{2}=a^{2}+2 a b+b^{2}} & {(a-b)(a+b)=a^{2}-b^{2}} \\ {(a-b)^{2}=a^{2}+2 a b+b^{2}} \\ {\text { - Squaring a binomial }}& {\text { - Multiplying conjugates }} \\ {\text { - Product is a trinomial }} & {\text { - Product is a binomial }} \\ {\text { - Inner and outer terms with FOIL are the same. }} &{\text { - Inner and outer terms with FOIL are opposites. }} \\ {\text { - Middle term is double the product of the terms. }} &{\text { - There is no middle term. }} \end{array}\)
选择合适的图案并使用它来查找产品:
- \((2 x-3)(2 x+3)\)
- \((8 x-5)^{2}\)
- \((6 m+7)^{2}\)
- \((5 x-6)(6 x+5)\)
解决方案:
1。 \((2x−3)(2x+3)\)这些是共轭物。 它们具有相同的第一个数字和相同的最后一个数字,一个二项式是总和,另一个是差值。 它符合共轭物乘积模式。
| 这符合图案。 | 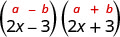 |
| 使用图案。 | 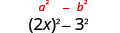 |
| 简化。 | \(4 x^{2}-9\) |
2。 \((8 x-5)^{2}\)我们被要求对二项式求平方。 它符合二项式方块图案。
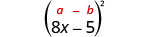 |
|
| 使用图案。 |  |
| 简化。 | \(64 x^{2}-80 x+25\) |
3。 \((6 m+7)^{2}\)同样,我们将对二项式进行平方,因此我们使用二项式方块图案。
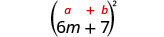 |
|
| 使用图案。 |  |
| 简化。 | \(36 m^{2}+84 m+49\) |
4。 \((5 x-6)(6 x+5)\)本产品不符合图案,因此我们将使用 FOIL。
\(\begin{array}{ll} & (5 x-6)(6 x+5)\\ {\text { Use FOIL. }} & {30 x^{2}+25 x-36 x-30} \\ {\text { Simplify. }} & {30 x^{2}-11 x-30}\end{array}\)
选择合适的图案并使用它来查找产品:
- \((9b−2)(2b+9)\)
- \((9p−4)2\)
- \((7y+1)^2\)
- \((4r-3)(4r+3)\)
- 回答
-
- 铝箔;\(18 b^{2}+77 b-18\)
- 二项式方块;\(81 p^{2}-72 p+16\)
- 二项式方块;\(49 y^{2}+14 y+1\)
- 偶联物的产物;\(16 r^{2}-9\)
选择合适的图案并使用它来查找产品:
- \((6x+7)^2\)
- \((3x−4)(3x+4)\)
- \((2x−5)(5x−2)\)
- \((6n−1)^2\)
- 回答
-
- 二项式方块;\(36 x^{2}+84 x+49\)
- 偶联物的产物;\(9 x^{2}-16\)
- 铝箔;\(10 x^{2}-29 x+10\)
- 二项式方块;\(36 n^{2}-12 n+1\)
访问以下在线资源,获取有关特殊产品的更多指导和练习:
- 特殊产品
关键概念
- 二项式方块图案
- 如果 a、b 是实数,
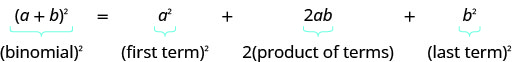
- \((a+b)^{2}=a^{2}+2 a b+b^{2}\)
- \((a-b)^{2}=a^{2}-2 a b+b^{2}\)
- 对二项式求平方:将第一个项求平方,将最后一个项求平方,将其乘积加倍。
- 如果 a、b 是实数,
- 共轭物图案的乘积
- 如果 a、ba、b 是实数,
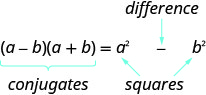
- \((a-b)(a+b)=a^{2}-b^{2}\)
- 该乘积称为平方差。
- 如果 a、ba、b 是实数,
- 要乘以共轭物:
- s@@ quare 第一个术语的平方最后一个术语把它写成平方差
词汇表
- 共轭对
- 共轭对是两个形式\((a−b)\)为 and 的二项式\((a+b)\);两对二项式的第一个项和最后一个项相同,但是一个二项式是总和,另一个是差值。


