6.1：加减多项式

学习目标

在本节结束时，您将能够：

• 识别多项式、单项式、二项式和三项式
• 确定多项式的次数
• 加减单项式
• 加减多项式
• 计算给定值的多项式

测验

在开始之前，请参加这个准备测验。

1. 简化：\(8x+3x\)。
   如果您错过了此问题，请查看练习 1.3.37。
2. 减去：\((5n+8)−(2n−1)\)。
   如果你错过了这个问题，请查看练习 1.10.52。
3. 以扩展形式写入:\(a^{5}\).
   如果您错过了此问题，请查看练习 1.3.7。

识别多项式、单项式、二项式和三项式

你已经知道一个项是一个常量或一个常量与一个或多个变量的乘积。 当其形式\(ax^{m}\)为常量\(m\)且\(a\)为整数时，它被称为单项式。 单项式的一些示例是\(8,−2x^{2},4y^{3}\)、和\(11z^{7}\)。

定义：单项式

单项式是形式的项\(ax^{m}\)，其中\(a\)是常数，\(m\)是正整数。

单项式或通过加法或减法组合的两个或多个单项式是多项式。 有些多项式根据项数有特殊的名称。 单项式是只有一个项的多项式。 二项式正好有两个项，而一个三项式正好有三个项。 超过三个项的多项式没有特殊名称。

定义：多项式

• 多项式 —单项式或通过加法或减法组合的两个或多个单项式是多项式。
• 单项式 —只有一个项的多项式称为单项式。
• 二项式 —正好有两个项的多项式称为二项式。
• 三项式 —正好有三个项的多项式称为三项式。

以下是多项式的一些示例。

\[\begin{array}{lllll}{\text { Polynomial }} & {b+1} &{4 y^{2}-7 y+2} & {4 x^{4}+x^{3}+8 x^{2}-9 x+1} \\ {\text { Monomial }} & {14} & {8 y^{2}} & {-9 x^{3} y^{5}} & {-13}\\ {\text { Binomial }} & {a+7}&{4 b-5} & {y^{2}-16}& {3 x^{3}-9 x^{2}} \\ {\text { Trinomial }} & {x^{2}-7 x+12} & {9 y^{2}+2 y-8} & {6 m^{4}-m^{3}+8 m}&{z^{4}+3 z^{2}-1} \end{array} \nonumber\]

请注意，每个单项式、二项式和三项式也是多项式。 它们只是多项式 “家族” 中的特殊成员，因此它们有特殊的名字。 我们在提及这些特殊多项式时使用单项式、二项式和三项式这两个词，然后将其余所有多项式称为即可。

示例\(\PageIndex{1}\)

确定每个多项式是单项式、二项式、三项式还是其他多项式。

1. \(4y^{2}−8y−6\)
2. \(−5a^{4}b^{2}\)
3. \(2x^{5}−5x^{3}−3x + 4\)
4. \(13−5m^{3}\)
5. q

回答

\(\begin{array}{lll}&{\text { Polynomial }} & {\text { Number of terms }} & {\text { Type }} \\ {\text { (a) }} & {4 y^{2}-8 y-6} & {3} & {\text { Trinomial }} \\ {\text { (b) }} & {-5 a^{4} b^{2}} & {1} & {\text { Monomial }} \\ {\text { (c) }} & {2 x^{5}-5 x^{3}-9 x^{2}+3 x+4} & {5} & {\text { Ponomial }} \\ {\text { (d) }} & {13-5 m^{3}} & {2} & {\text { Binomial }} \\ {\text { (e) }} & {q} & {1} & {\text { Monomial }}\end{array}\)

示例\(\PageIndex{2}\)

确定每个多项式是单项式、二项式、三项式还是其他多项式：

1. 5b
2. \(8 y^{3}-7 y^{2}-y-3\)
3. \(-3 x^{2}-5 x+9\)
4. \(81-4 a^{2}\)
5. \(-5 x^{6}\)

回答

1. 单项式
2. 多项式
3. 三项式
4. 二项式
5. 单项式

示例\(\PageIndex{3}\)

确定每个多项式是单项式、二项式、三项式还是其他多项式：

1. \(27 z^{3}-8\)
2. \(12 m^{3}-5 m^{2}-2 m\)
3. \(\frac{5}{6}\)
4. \(8 x^{4}-7 x^{2}-6 x-5\)
5. \(-n^{4}\)

回答

1. 二项式
2. 三项式
3. 单项式
4. 多项式
5. 单项式

确定多项式的次数

多项式的次数及其项的次数由变量的指数决定。 没有变量，只有常量的单项式是一种特例。 常数的度数为 0，也就是说，它没有变量。

定义：多项式的次数

• 项的度数是其变量的指数之和。
• 常数的度数为 0。
• 多项式的次数是其所有项的最高度。

让我们通过看几个多项式来看看它是如何工作的。 我们将逐步进行，从单项式开始，然后发展到具有更多项的多项式。

当多项式的项按度降序书写时，多项式为标准形式。 养成先写最高学位的学期的习惯。

示例\(\PageIndex{4}\)

找出以下多项式的次数。

1. 10y
2. \(4 x^{3}-7 x+5\)
3. −15
4. \(-8 b^{2}+9 b-2\)
5. \(8 x y^{2}+2 y\)

回答

1. \(\begin{array}{ll} & 10y\\ \text{The exponent of y is one. } y=y^1 & \text{The degree is 1.}\end{array}\)
2. \(\begin{array}{ll} & 4 x^{3}-7 x+5\\ \text{The highest degree of all the terms is 3.} & \text{The degree is 3.}\end{array}\)
3. \(\begin{array}{ll} & -15\\ \text{The degree of a constant is 0.} & \text{The degree is 0.}\end{array}\)
4. \(\begin{array}{ll} & -8 b^{2}+9 b-2\\ \text{The highest degree of all the terms is 2.} & \text{The degree is 2.}\end{array}\)
5. \(\begin{array}{ll} & 8 x y^{2}+2 y\\ \text{The highest degree of all the terms is 3.} & \text{The degree is 3.}\end{array}\)

示例\(\PageIndex{5}\)

求出以下多项式的次数：

1. −15b
2. \(10 z^{4}+4 z^{2}-5\)
3. \(12 c^{5} d^{4}+9 c^{3} d^{9}-7\)
4. \(3 x^{2} y-4 x\)
5. −9

回答

1. 1
2. 4
3. 12
4. 3
5. 0

示例\(\PageIndex{6}\)

求出以下多项式的次数：

1. 52
2. \(a^{4} b-17 a^{4}\)
3. \(5 x+6 y+2 z\)
4. \(3 x^{2}-5 x+7\)
5. \(-a^{3}\)

回答

1. 0
2. 5
3. 1
4. 2
5. 3

加减单项式

你已经学会了如何通过组合相似的术语来简化表达式。 请记住，类似项必须具有相同的变量和相同的指数。 由于单项式是术语，因此加减单项式与合并相似项相同。 如果单项式与项类似，我们只需将它们相加或减去系数即可。

示例\(\PageIndex{7}\)

添加：\(25 y^{2}+15 y^{2}\)

回答

\(\begin{array}{ll} & 25 y^{2}+15 y^{2}\\ \text{Combine like terms.} & 40y^{2}\end{array}\)

示例\(\PageIndex{8}\)

添加：\(12 q^{2}+9 q^{2}\)

回答

21\(q^{2}\)

示例\(\PageIndex{9}\)

添加：\(-15 c^{2}+8 c^{2}\)

回答

\(-7 c^{2}\)

示例\(\PageIndex{10}\)

减去：16p− (−7p)

回答

\(\begin{array}{ll} & 16p−(−7p) \\ \text{Combine like terms.} & 23p\end{array}\)

示例\(\PageIndex{11}\)

减去：8m− (−5m)。

回答

13m

示例\(\PageIndex{12}\)

减去：\(-15 z^{3}-\left(-5 z^{3}\right)\)

回答

\(-10 z^{3}\)

请记住，相似项必须具有相同的变量和相同的指数。

示例\(\PageIndex{13}\)

简化：\(c^{2}+7 d^{2}-6 c^{2}\)

回答

\(\begin{array}{ll} & c^{2}+7 d^{2}-6 c^{2} \\ \text{Combine like terms.} & -5 c^{2}+7 d^{2} \end{array}\)

示例\(\PageIndex{14}\)

添加：\(8 y^{2}+3 z^{2}-3 y^{2}\)

回答

\(5 y^{2}+3 z^{2}\)

示例\(\PageIndex{15}\)

添加：\(3 m^{2}+n^{2}-7 m^{2}\)

回答

\(-4 m^{2}+n^{2}\)

示例\(\PageIndex{16}\)

简化：\(u^{2} v+5 u^{2}-3 v^{2}\)

回答

\ (\ begin {array} {ll} &u^ {2} v+5 u^ {2} -3 v^ {2}
\\\ text {没有类似的术语可以合并。} & u^ {2} v+5 u^ {2} -3 v^ {2}\ end {array}\)

示例\(\PageIndex{17}\)

简化：\(m^{2} n^{2}-8 m^{2}+4 n^{2}\)

回答

没有相似的术语可以合并。

示例\(\PageIndex{18}\)

简化：\(p q^{2}-6 p-5 q^{2}\)

回答

没有相似的术语可以合并。

加减多项式

我们可以将加减多项式看作是将一系列单项式相加和减去。 寻找相似的术语——那些具有相同变量和相同指数的术语。 Commutative Property 允许我们重新排列条款，将相似的术语组合在一起。

示例\(\PageIndex{19}\)

找到总和：\(\left(5 y^{2}-3 y+15\right)+\left(3 y^{2}-4 y-11\right)\)

回答

识别相似的术语。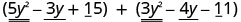
重新排列以将相似的术语整合在一起。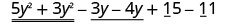
将相似的术语组合在一起。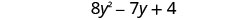

示例\(\PageIndex{20}\)

找到总和：\(\left(7 x^{2}-4 x+5\right)+\left(x^{2}-7 x+3\right)\)

回答

\(8 x^{2}-11 x+1\)

示例\(\PageIndex{21}\)

找到总和：\(\left(14 y^{2}+6 y-4\right)+\left(3 y^{2}+8 y+5\right)\)

回答

\(17 y^{2}+14 y+1\)

示例\(\PageIndex{22}\)

找出区别：\(\left(9 w^{2}-7 w+5\right)-\left(2 w^{2}-4\right)\)

回答

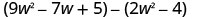
分发和识别相似的术语。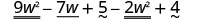
重新排列条款。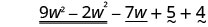
将相似的术语组合在一起。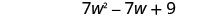

示例\(\PageIndex{23}\)

找出区别：\(\left(8 x^{2}+3 x-19\right)-\left(7 x^{2}-14\right)\)

回答

\(15 x^{2}+3 x-5\)

示例\(\PageIndex{24}\)

找出区别：\(\left(9 b^{2}-5 b-4\right)-\left(3 b^{2}-5 b-7\right)\)

回答

\(6 b^{2}+3\)

示例\(\PageIndex{25}\)

减去：\(\left(c^{2}-4 c+7\right)\)从\(\left(7 c^{2}-5 c+3\right)\)

回答

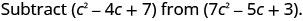
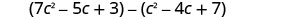
分发和识别相似的术语。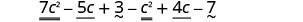
重新排列条款。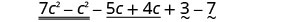
将相似的术语组合在一起。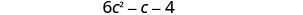

示例\(\PageIndex{26}\)

减去：\(\left(5 z^{2}-6 z-2\right)\)从\(\left(7 z^{2}+6 z-4\right)\)

回答

\(2 z^{2}+12 z-2\)

示例\(\PageIndex{27}\)

减去：\(\left(x^{2}-5 x-8\right)\)从\(\left(6 x^{2}+9 x-1\right)\)

回答

\(5 x^{2}+14 x+7\)

示例\(\PageIndex{28}\)

找到总和：\(\left(u^{2}-6 u v+5 v^{2}\right)+\left(3 u^{2}+2 u v\right)\)

回答

\(\begin{array} {ll} & {\left(u^{2}-6 u v+5 v^{2}\right)+\left(3 u^{2}+2 u v\right)} \\\text{Distribute.} & {u^{2}-6 u v+5 v^{2}+3 u^{2}+2 u v} \\ \text{Rearrange the terms, to put like terms together} & {u^{2}+3 u^{2}-6 u v+2 u v+5 v^{2}} \\ \text{Combine like terms.} & {4 u^{2}-4 u v+5 v^{2}}\end{array}\)

示例\(\PageIndex{29}\)

找到总和：\(\left(3 x^{2}-4 x y+5 y^{2}\right)+\left(2 x^{2}-x y\right)\)

回答

\(5 x^{2}-5 x y+5 y^{2}\)

示例\(\PageIndex{30}\)

找到总和：\(\left(2 x^{2}-3 x y-2 y^{2}\right)+\left(5 x^{2}-3 x y\right)\)

回答

\(7 x^{2}-6 x y-2 y^{2}\)

示例\(\PageIndex{31}\)

找出区别：\(\left(p^{2}+q^{2}\right)-\left(p^{2}+10 p q-2 q^{2}\right)\)

回答

\(\begin{array}{ll} & {\left(p^{2}+q^{2}\right)-\left(p^{2}+10 p q-2 q^{2}\right)} \\ \text{Distribute.} &{p^{2}+q^{2}-p^{2}-10 p q+2 q^{2}} \\\text{Rearrange the terms, to put like terms together} & {p^{2}-p^{2}-10 p q+q^{2}+2 q^{2}} \\\text{Combine like terms.} & {-10 p q+3 q^{2}}\end{array}\)

示例\(\PageIndex{32}\)

找出区别：\(\left(a^{2}+b^{2}\right)-\left(a^{2}+5 a b-6 b^{2}\right)\)

回答

\(-5 a b-5 b^{2}\)

示例\(\PageIndex{33}\)

找出区别：\(\left(m^{2}+n^{2}\right)-\left(m^{2}-7 m n-3 n^{2}\right)\)

回答

\(4 n^{2}+7 m n\)

示例\(\PageIndex{34}\)

简化：\(\left(a^{3}-a^{2} b\right)-\left(a b^{2}+b^{3}\right)+\left(a^{2} b+a b^{2}\right)\)

回答

\(\begin{array}{ll } & {\left(a^{3}-a^{2} b\right)-\left(a b^{2}+b^{3}\right)+\left(a^{2} b+a b^{2}\right)} \\ \text{Distribute.} &{a^{3}-a^{2} b-a b^{2}-b^{3}+a^{2} b+a b^{2}} \\ \text{Rearrange the terms, to put like terms together} & {a^{3}-a^{2} b+a^{2} b-a b^{2}+a b^{2}-b^{3}} \\ \text{Combine like terms.} &{a^{3}-b^{3}}\end{array}\)

示例\(\PageIndex{35}\)

简化：\(\left(x^{3}-x^{2} y\right)-\left(x y^{2}+y^{3}\right)+\left(x^{2} y+x y^{2}\right)\)

回答

\(x^{3}-y^{3}\)

示例\(\PageIndex{36}\)

简化：\(\left(p^{3}-p^{2} q\right)+\left(p q^{2}+q^{3}\right)-\left(p^{2} q+p q^{2}\right)\)

回答

\(p^{3}-2 p^{2} q+q^{3}\)

计算给定值的多项式

我们已经学会了如何计算表达式。 由于多项式是表达式，因此我们将按照相同的程序来计算多项式。 我们将用给定值代替变量，然后使用运算顺序进行简化。

示例\(\PageIndex{37}\)

评估\(5x^{2}−8x+4\)何时

1. x=4
2. x=−2
3. x=0

回答

1. x=4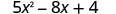
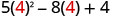
简化指数。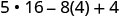
乘以。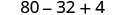
简化。

2. x=−2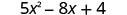
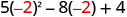
简化指数。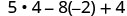
乘以。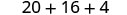
简化。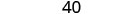

3. x=0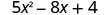
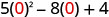
简化指数。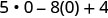
乘以。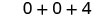
简化。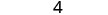

示例\(\PageIndex{38}\)

评估：\(3x^{2}+2x−15\)何时

1. x=3
2. x=−5
3. x=0

回答

1. 18
2. 50
3. −15

示例\(\PageIndex{39}\)

评估：\(5z^{2}−z−4\)何时

1. z=−2
2. z=0
3. z=2

回答

1. 18
2. −4
3. 14

示例\(\PageIndex{40}\)

多项式\(−16t^{2}+250\)给出了球从 250 英尺高的建筑物掉落后的几秒钟的高度。 在 t=2 秒后找出高度。

回答

\(\begin{array}{ll } & −16t^{2}+250 \\ \text{Substitute t = 2.} & -16(2)^{2} + 250 \\ \text{Simplify }& −16\cdot 4+250 \\ \text{Simplify }& -64 + 250\\ \text{Simplify }& 186 \\& \text{After 2 seconds the height of the ball is 186 feet. } \end{array}\)

示例\(\PageIndex{41}\)

多项式\(−16t^{2}+250\)给出了球从 250 英尺高的建筑物掉落后的几秒钟的高度。 在 t=0 秒后找出高度。

回答

250

示例\(\PageIndex{42}\)

多项式\(−16t^{2}+250\)给出了球从 250 英尺高的建筑物掉落后的几秒钟的高度。 在 t=3 秒后找出高度。

回答

106

示例\(\PageIndex{43}\)

多项式\(6x^{2}+15xy\)给出了生产矩形容器的成本（以美元为单位），该容器的顶部和底部是正方形，边长为 x 英尺，边高为 y 英尺。 找出生产一个 x=4 英尺和 y=6y=6 英尺的盒子的成本。

回答

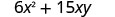
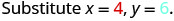
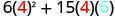
简化。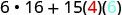
简化。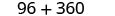
简化。
	生产这个盒子的成本为456美元。

示例\(\PageIndex{43}\)

多项式\(6x^{2}+15xy\)给出了生产矩形容器的成本（以美元为单位），该容器的顶部和底部是正方形，边长为 x 英尺，边高为 y 英尺。 找出生产一个 x=6 英尺和 y=4 英尺的盒子的成本。

回答

576 美元

示例\(\PageIndex{44}\)

多项式\(6x^{2}+15xy\)给出了生产矩形容器的成本（以美元为单位），该容器的顶部和底部是正方形，边长为 x 英尺，边高为 y 英尺。 找出生产一个 x=5 英尺和 y=8 英尺的盒子的成本。

回答

750 美元

关键概念

• 单项式
  • 单项式是形式的术语\(ax^{m}\)，其中 aa 是常数，mm 是整数
    
• 多项式
  • 多项式 —通过加法或减法组合的单项式或两个或多个单项式是多项式。
  • 单项式 —只有一个项的多项式称为单项式。
  • 二项式 —正好有两个项的多项式称为二项式。
  • 三项式 —正好有三个项的多项式称为三项式。
    
• 多项式的次数
  • 项的度数是其变量的指数之和。
  • 常数的度数为 0。
  • 多项式的次数是其所有项的最高度。

词汇表

二项式

二项式是正好有两个项的多项式。

常数的度

任何常数的度数均为 0。

多项式的次数

多项式的次数是其所有项的最高度。

一个术语的学位

项的度数是其变量的指数。

单项式

单项式是形式的项\(ax^m\)，其中 a 是常数，m 是整数；单项式正好有一个项。

多项式

多项式是单项式，或通过加法或减法组合的两个或多个单项式。

标准表单

当多项式的项按度降序书写时，多项式为标准形式。

三项式

三项式是正好有三个项的多项式。