5.1：通过绘图求解方程组

Last updated
Save as PDF

Page ID: 204388

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

学习目标

在本节结束时，您将能够：

确定有序对是否是方程组的解
通过绘图求解线性方程组
确定线性系统的解数
通过绘图求解方程组的应用

注意

在开始之前，请参加这个准备测验。

对于方程$y=\frac{2}{3}x−4$
ⓐ (6,0) 是解吗？ ⓑ (−3, −2) 是解决方案吗？
如果您错过了此问题，请查看练习 2.1.1。
找出直线 3x−y=12 的斜率和 y 截距。
如果您错过了此问题，请查看练习 4.5.7。
找出 2x−3y=12 线的 x 和 y 截距。
如果您错过了此问题，请查看练习 4.3.7。

确定有序对是否是方程组的解

在求解线性方程和不等式部分中，我们学习了如何用一个变量求解线性方程。请记住，方程的解是变量的值，当它被替换到方程中时，该变量的陈述是真实的。现在我们将使用线性方程组，即组合在一起的两个或多个线性方程组。

定义：线性方程组

当两个或多个线性方程组合在一起时，它们形成线性方程组。

我们将把工作重点放在两个未知数中的两个线性方程组上。稍后，你可以求解更大的方程组。

两个线性方程组的示例如下所示。我们用大括号表示两个方程组合在一起形成方程组。

\[\begin{cases}{2 x+y=7} \\ {x-2 y=6}\end{cases}\]

由两个变量组成的线性方程，例如 2 x + y = 7，具有无限数量的解。它的图形是一条线。请记住，直线上的每个点都是方程的解，方程的每个解都是直线上的一个点。

为了求解一个由两个线性方程组成的系统，我们想找出作为两个方程解的变量的值。换句话说，我们正在寻找使两个方程都成真的有序对（x，y）。这些被称为方程组的解。

定义：方程组的解

方程组的解是使所有方程成真的变量的值。两个线性方程组的解由有序对 (x, y) 表示。

为了确定有序对是否是两个方程组的解，我们将变量的值代入每个方程中。如果有序对使两个方程都成立，则这是方程的解。

让我们考虑下面的系统：

\[\begin{cases}{3x−y=7} \\ {x−2y=4}\end{cases}\]

有序对（2，−1）是解决方案吗？

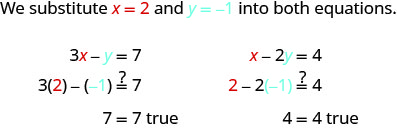
$这个数字以一句话开头，“我们在两个方程中都用 x =2 和 y = -1 代替。” 第一个方程显示 3x 减去 y 等于 7。然后 3 乘以 2 减去负数，在括号中等于 7。那么 7 等于 7 是真的。第二个方程读取 x 减去 2y 等于 4。然后 2 减去 2 乘以括号中的负数等于 4。那么 4 = 4 是真的。$

有序对 (2, −1) 使两个方程都成真。因此 (2, −1) 是这个系统的解。

让我们试试另一对订购的鞋子。订购的货币对（3，2）是解决方案吗？

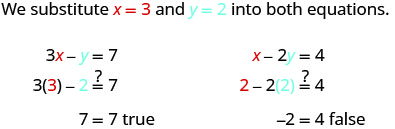
$这个数字以 “我们在两个方程中替换 x 等于 3 和 y 等于 2” 这句话开头。第一个方程读取 3 倍 x 减去 7 等于 7。然后，3 乘以 3 减去 2 等于 7。那么 7 = 7 是真的。第二个方程读取 x 减去 2y 等于 4。 n 倍 2 减去 2 倍 2 = 4。那么负数 2 = 4 是假的。$

有序对 (3, 2) 使一个方程成真，但它使另一个方程变为错误。由于它不是两个方程的解，因此它不是该系统的解。

练习$\PageIndex{1}$

确定订购的配对是否是系统的解决方案：$\begin{cases}{x−y=−1} \\ {2x−y=−5}\end{cases}$

(−2、−1)
(−4、−3)

回答: 1。
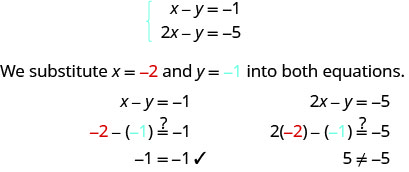
$此图显示了两个带括号的方程。第一个是 x 减去 y = 负 1。第二个是 2 倍 x 减去 y 等于负 5。接下来是 “我们在两个方程中用 x = 负 2 和 y = 1 替换” 这句话。第一个方程显示了替换，并显示了负 1 = 负 1。第二个方程显示替换，并显示 5 不等于 -5。第一个方程之下有一句话：“（负 2，负 1）不能使两个方程都成真。” 第二个方程下有一句话：“（负 2，负 1）不是解。”$
(−2, −1) 不能使两个方程都成真。(−2, −1) 不是解。

2。
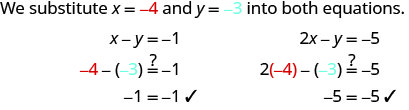
$这个数字以这句话开头：“我们在两个方程中都用 x = -4 和 y = -3 代替。” 列出的第一个方程显示 x — y = -1。然后 -4-(-3) = -1。然后 -1 = -1。列出的第二个方程显示 2x — y = -5。然后是 2 次 (-4) — (-3) = -5。然后 -5 = -5。第一个方程下有一句话：“(-4, -3) 确实使两个方程都成真。” 第二个方程下方是 “(-4, -3) 是解” 这句话。$
(−4, −3) 不能使两个方程都成立。(−4, −3) 是一个解。

练习$\PageIndex{2}$

确定订购的配对是否是系统的解决方案：$\begin{cases}{3x+y=0} \\ {x+2y=−5}\end{cases}$

(1, −3)
(0,0)

回答

是的
不

练习$\PageIndex{3}$

确定订购的配对是否是系统的解决方案：$\begin{cases}{x−3y=−8} \\ {−3x−y=4}\end{cases}$

(2, −2)
(−2,2)

回答

不
是的

通过绘图求解线性方程组

在本章中，我们将使用三种方法来求解线性方程组。我们将使用的第一种方法是绘图。线性方程的图形是一条直线。直线上的每个点都是方程的解。对于由两个方程组成的系统，我们将绘制两条直线。然后我们可以看到作为每个方程解的所有点。而且，通过找到这些线路的共同点，我们将找到系统的解决方案。

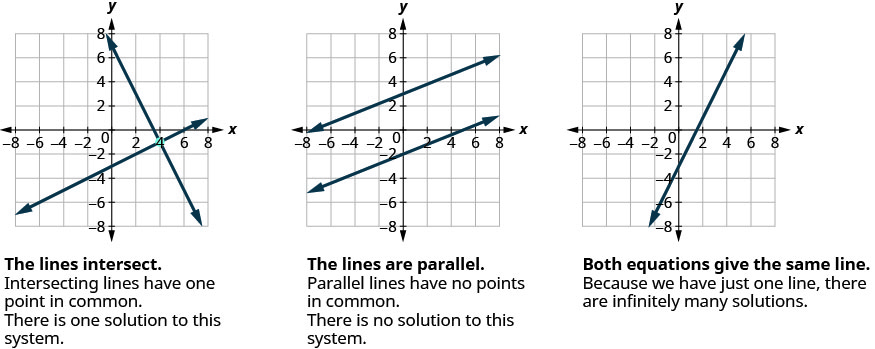
一个变量中的大多数线性方程都有一个解，但是我们看到一些称为矛盾的方程没有解，而对于其他称为恒等式的方程，所有数字都是解。同样，当我们求解由两个线性方程组成的系统时，由同一平面中的两条线形表示的线性方程组时，有三种可能的情况，如图所示$\PageIndex{1}$：

此图显示了三个 x y 坐标平面。第一个平面显示了两条在一个点上相交的直线。在图表下方写着：“线条相交。相交线有一个共同点。这个系统有一个解决方案。” 第二个 x y 坐标平面显示两条平行线。在图表下方写着：“线是平行的。平行线没有共同点。这个系统没有解决办法。” 第三个 x y 坐标平面显示一条直线。在图表下方写着：“两个方程给出相同的直线。因为我们只有一条线，所以有无限多的解决方案。” — 图$\PageIndex{1}$

对于本节和接下来的两节中求解线性方程组的第一个示例，我们将求解由两个线性方程组成的同一个方程组。但是我们将在每个部分中使用不同的方法。看完第三种方法后，你将决定哪种方法是解决这个系统的最便捷的方法。

练习$\PageIndex{4}$: How to Solve a System of Linear Equations by Graphing

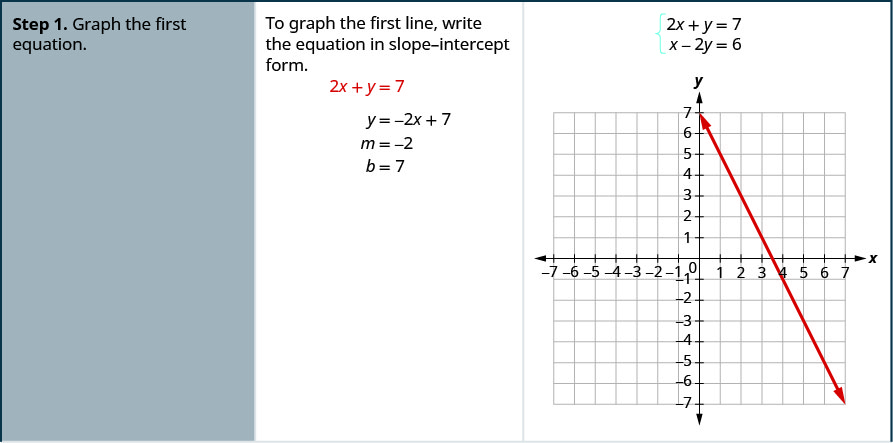
通过绘制图表求解系统：$\begin{cases}{2x+y=7} \\ {x−2y=6}\end{cases}$

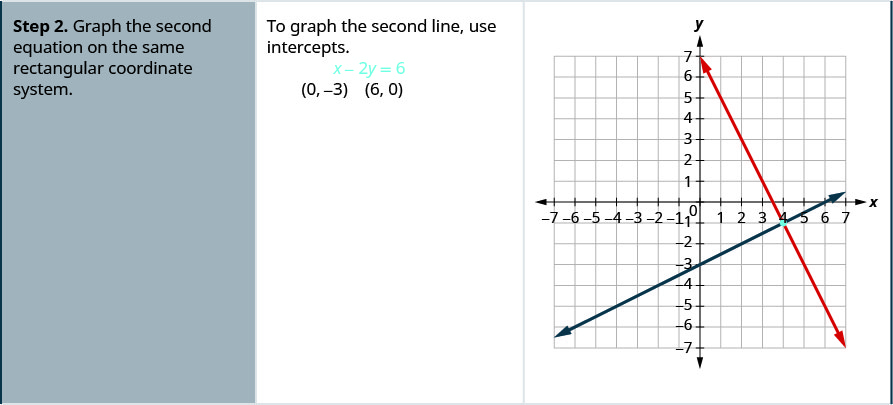
回答: $此表有四行三列。第一列充当标题列。第一行显示为 “步骤 1。绘制第一个方程的图表。” 然后它写着：“要绘制第一条线，请用斜率截距的形式写出方程。” 方程读取 2x + y = 7，变成 y = -2x + 7，其中 m = -2，b = 7。然后它显示了 2x + y = 7 的方程图。还列出了方程 x — 2y = 6。$ $第二行显示为 “第 2 步。在同一个直角坐标系上绘制第二个方程的图形。” 然后它说：“要绘制第二条线，请使用截图。” 后面是方程 x — 2y = 6 以及有序对 (0, -3) 和 (6, 0)。该行的最后一列显示了两个方程的图形。$ $第三行是：“第 3 步。确定两条线是相交、平行还是同一条线。” 然后 “看看线条图。” 最后它写着：“线条相交。”$ $第四行是：“第 4 步。确定系统的解决方案。如果两条线相交，请确定交点。检查以确保它是两个方程的解。这是系统的解决方案。如果线是平行的，则系统没有解决方案。如果两条线相同，则系统有无限数量的解。” 然后它写着：“由于线条相交，请找到交点。检查两个方程中的点。” 最后它写着：“线条在 (4, -1) 处相交。然后它使用替换来表明 “解是 (4, -1)”。$

练习$\PageIndex{5}$

通过绘制图表求解每个系统：$\begin{cases}{x−3y=−3} \\ {x+y=5}\end{cases}$

回答: (3,2)

练习$\PageIndex{6}$

通过绘制图表求解每个系统：$\begin{cases}{−x+y=1} \\ {3x+2y=12}\end{cases}$

回答: (2,3)

通过图表求解线性方程组的步骤如下所示。

通过绘图求解线性方程组。

绘制第一个方程的图形。
在同一个直角坐标系上绘制第二个方程的图形。
确定两条线是相交、平行还是同一条线。
确定系统的解决方案。
- 如果两条线相交，请确定交点。检查以确保它是两个方程的解。这是系统的解决方案。
- 如果线是平行的，则系统没有解决方案。
- 如果两条线相同，则系统有无限数量的解。

练习$\PageIndex{7}$

通过绘制图表求解系统：$\begin{cases}{y=2x+1} \\ {y=4x−1}\end{cases}$

回答

该系统中的两个方程都是斜率截距形式，因此我们将使用它们的斜率和 y 截距来绘制它们的图形。 $\begin{cases}{y=2x+1} \\ {y=4x−1}\end{cases}$

求出第一个方程的斜率和 y 截距。	$。$
求出第一个方程的斜率和 y 截距。	$。$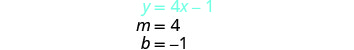
绘制这两条线的图形。
确定交叉点。	线在 (1, 3) 处相交。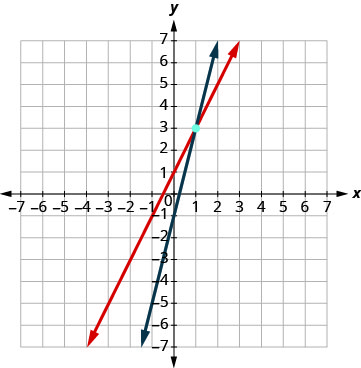
	$。$
检查两个方程中的解。	$\begin{array}{l}{y=2 x+1} & {y = 4x - 1}\\{3\stackrel{?}{=}2 \cdot 1+1} &{3\stackrel{?}{=}4 \cdot 1-1} \\ {3=3 \checkmark}&{3=3 \checkmark} \end{array}$
	解决方案是 (1, 3)。

练习$\PageIndex{8}$

通过绘制图表求解系统：$\begin{cases}{y=2x+2} \\ {y=-x−4}\end{cases}$

回答: (−2、−2)

练习$\PageIndex{9}$

通过绘制图表求解系统：$\begin{cases}{y=3x+3} \\ {y=-x+7}\end{cases}$

回答: (1,6)

练习$\PageIndex{7}$中的两个方程均以斜率截距形式给出。这使我们可以轻松地快速绘制线条。在下一个示例中，我们将首先将方程重写为斜率截距形式。

练习$\PageIndex{10}$

通过绘制图表求解系统：$\begin{cases}{3x+y=−1} \\ {2x+y=0}\end{cases}$

回答

我们将为这两个方程求解 yy，这样我们就可以使用它们的斜率和 y 截距轻松绘制它们的图形。 $\begin{cases}{3x+y=−1} \\ {2x+y=0}\end{cases}$

求解 y 的第一个方程。找出斜率和 y 截距。求解 y 的第二个方程。找出斜率和 y 截距。	$\begin{aligned} 3 x+y &=-1 \\ y &=-3 x-1 \\ m &=-3 \\ b &=-1 \\ 2 x+y &=0 \\ y &=-2 x \\ b &=0 \end{aligned}$
绘制线条图。	$。$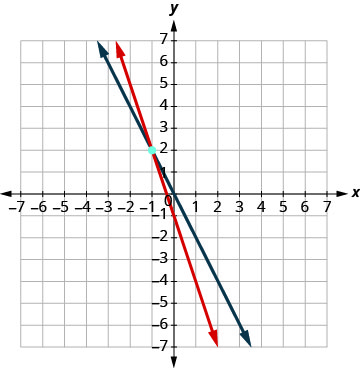
确定交叉点。	两条线在 (−1, 2) 处相交。
检查两个方程中的解。	$\begin{array}{rllrll}{3x+y}&{=}&{-1} & {2x +y}&{=}&{0}\\{3(-1)+ 2}&{\stackrel{?}{=}}&{-1} &{2(-1)+2}&{\stackrel{?}{=}}&{0} \\ {-1}&{=}&{-1 \checkmark}&{0}&{=}&{0 \checkmark} \end{array}$
	解是 (−1, 2)。

练习$\PageIndex{11}$

通过绘制图表求解每个系统：$\begin{cases}{−x+y=1} \\ {2x+y=10}\end{cases}$

回答: (3,4)

练习$\PageIndex{12}$

通过绘制图表求解每个系统：$\begin{cases}{ 2x+y=6} \\ {x+y=1}\end{cases}$

回答: (5, −4)

通常，当方程以标准形式给出时，绘制方程的最便捷方法是使用截距。我们将在练习中做到这一点$\PageIndex{13}$。

练习$\PageIndex{13}$

通过绘制图表求解系统：$\begin{cases}{x+y=2} \\ {x−y=4}\end{cases}$

回答

我们将找到两个方程的 x 和 y 截距，然后用它们绘制线条图。

	$。$
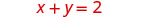
要找到截距，让 x = 0 求解 y，然后让 y = 0 求解 x。	$\begin{aligned} x+y &=2 \quad x+y=2 \\ 0+y &=2 \quad x+0=2 \\ y &=2 \quad x=2 \end{aligned}$	$。$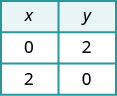
	$。$
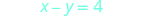
要找到截取次数，假设 x = 0 然后让 y = 0。	\ begin {array} {rlr} {x-y} & {=4} & {x-y} & {= 4}\\ {0-y} & {=4} & {x-0} & {=4}\\ {-y} & {=4}\\ {y} & {=4}\\\ {y}\ end {array}	$。$
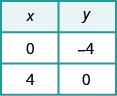
绘制线条图。	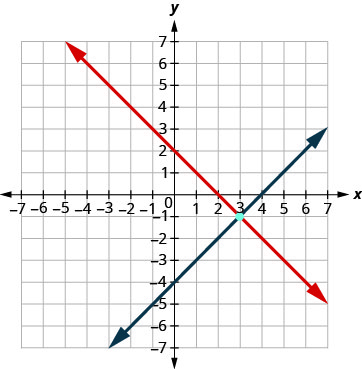$此图显示了两条直线在 x y 坐标平面上的点 (3, -1) 处的交点。$
确定交叉点。	线在 (3, −1) 处相交。
检查两个方程中的解。	$\begin{array}{rllrll}{x+y}&{=}&{2} & {x-y}&{=}&{4}\\{3+(-1)}&{\stackrel{?}{=}}&{2} &{3 - (-1)}&{\stackrel{?}{=}}&{4} \\ {2}&{=}&{2 \checkmark}&{4}&{=}&{4 \checkmark} \end{array}$ 解是 (3, −1)。

练习$\PageIndex{14}$

通过绘制图表求解每个系统：$\begin{cases}{x+y=6} \\ {x−y=2}\end{cases}$

回答: (4,2)

练习$\PageIndex{15}$

通过绘制图表求解每个系统：$\begin{cases}{x+y=2} \\ {x−y=-8}\end{cases}$

回答: (5, −3)

你还记得如何用一个变量绘制线性方程吗？它将是垂直线或水平线。

练习$\PageIndex{16}$

通过绘制图表求解系统：$\begin{cases}{y=6} \\ {2x+3y=12}\end{cases}$

回答

	$。$
我们知道第一个方程代表一条水平线，其 y 截距为 6。	$。$
使用截距绘制第二个方程最为方便。	$。$
要找到截距，假设 x = 0，然后 y = 0。	$。$
绘制线条图。	$。$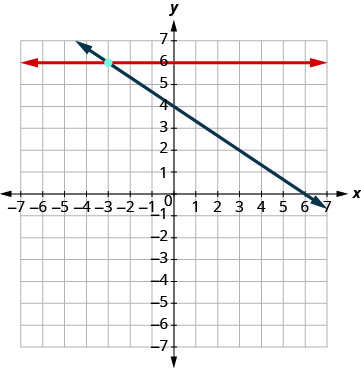
确定交叉点。	两条线在 (−3, 6) 处相交。
检查两个方程的解。	$\begin{array}{rllrll}{y}&{=}&{6} & {2x+3y}&{=}&{12}\\{6}&{\stackrel{?}{=}}&{6} &{2(-3) + 3(6)}&{\stackrel{?}{=}}&{12} \\ {6}&{=}&{6 \checkmark} &{-6+18}&{\stackrel{?}{=}}&{12} \\ {}&{}&{}&{12}&{=}&{12 \checkmark} \end{array}$
	解是 (−3, 6)。

练习$\PageIndex{17}$

通过绘制图表求解每个系统：$\begin{cases}{y=−1} \\ {x+3y=6}\end{cases}$

回答: (9, −1)

练习$\PageIndex{18}$

通过绘制图表求解每个系统：$\begin{cases}{x=4} \\ {3x−2y=24}\end{cases}$

回答: (4, −6)

到目前为止，在所有线性方程组中，直线相交，解为一个点。在接下来的两个示例中，我们将看一个没有解的方程组和一个具有无限个解的方程组。

练习$\PageIndex{19}$

通过绘制图表求解系统：$\begin{cases}{y=\frac{1}{2}x−3} \\ {x−2y=4}\end{cases}$

回答

	$。$
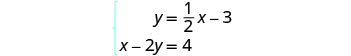
要绘制第一个方程，我们将使用其斜率和 y 截距。	$。$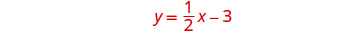
	$。$
	$。$
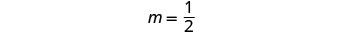
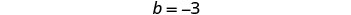
为了绘制第二个方程式，我们将使用截距。	$。$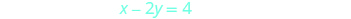
	$。$
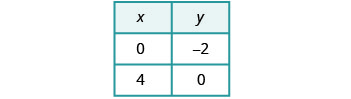
绘制线条图。	$。$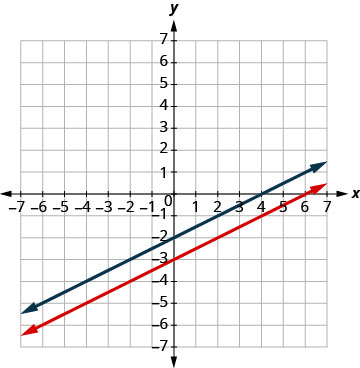
确定交叉点。	这些线是平行的。
	由于两条线上都没有点，因此没有使两个方程都成真的有序对。这个系统没有解决办法。

练习$\PageIndex{20}$

通过绘制图表求解每个系统：$\begin{cases}{y=-\frac{1}{4}x+2} \\ {x+4y=-8}\end{cases}$

回答: 没有解决办法

练习$\PageIndex{21}$

通过绘制图表求解每个系统：$\begin{cases}{y=3x−1} \\ {6x−2y=6}\end{cases}$

回答: 没有解决办法

练习$\PageIndex{22}$

通过绘制图表求解系统：$\begin{cases}{y=2x−3} \\ {−6x+3y=−9}\end{cases}$

回答

	$。$
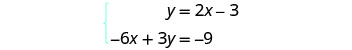
求出第一个方程的斜率和 y 截距。	$。$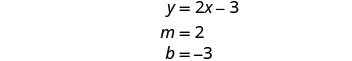
找出第二个方程的截距。	$。$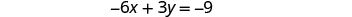
	$。$
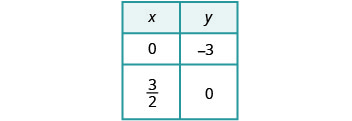
绘制线条图。	$。$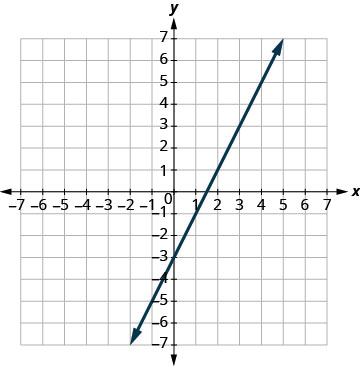
确定交叉点。	线条是一样的！
	由于直线上的每个点都使两个方程都成真，因此有无限多的有序对使两个方程都成真。
	这个系统有无限多的解决方案。

练习$\PageIndex{23}$

通过绘制图表求解每个系统：$\begin{cases}{y=−3x−6} \\ {6x+2y=−12}\end{cases}$

回答: 无限多的解决方案

练习$\PageIndex{24}$

通过绘制图表求解每个系统：$\begin{cases}{y=\frac{1}{2}x−4} \\ {2x−4y=16}\end{cases}$

回答: 无限多的解决方案

如果你在练习$\PageIndex{22}$中以斜率截距形式写出第二个方程，你可能会意识到这些方程具有相同的斜率和相同的 y 截距。

当我们在最后一个示例中绘制第二行时，我们将其绘制在第一行的正上方。我们说这两条线是重合的。重合线具有相同的斜率和相同的 y 截距。

重合线

重合线具有相同的斜率和相同的 y 截距。

确定线性系统的解数

有时我们会想知道线性方程组会有多少解，但实际上我们可能不必找到解。在不绘制图表的情况下确定这一点会很有帮助。

我们已经看到，同一个平面中的两条线要么相交，要么是平行的。 “$\PageIndex{4}$通过练习练习” 中的方程组$\PageIndex{16}$都有两条相交线。每个系统都有一个解决方案。

有平行线的系统，比如练习$\PageIndex{19}$，没有解决办法。运动中发生了什么$\PageIndex{22}$？方程有重合线，因此系统有无限多的解。

我们将在$\PageIndex{2}$下图中整理这些结果：

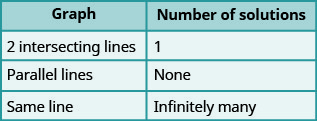
此表有两列和四行。第一行将每列标记为 “图形” 和 “解数”。 “图形” 下有 “2 条相交线”、“平行线” 和 “同一条线”。在 “解数” 下有 “1”、“无” 和 “无限多”。 — 图$\PageIndex{2}$

平行线的斜率相同，但 y 截距不同。因此，如果我们将两个方程以斜率截距的形式写入线性方程组中，我们可以看到没有绘制图表会有多少解！看看我们在练习中解决的系统$\PageIndex{19}$。

$\begin{array} {cc} & \begin{cases}{y=\frac{1}{2}x−3} \\ {x−2y=4}\end{cases}\\ \text{The first line is in slope–intercept form.} &\text { If we solve the second equation for } y, \text { we get } \\ &x-2 y =4 \\ y = \frac{1}{2}x -3& x-2 y =-x+4 \\ &y =\frac{1}{2} x-2 \\ m=\frac{1}{2}, b=-3&m=\frac{1}{2}, b=-2 \end{array}$

这两条线的斜率相同，但 y 截距不同。它们是平行线。

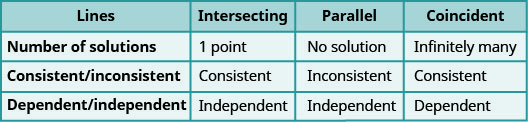
该图$\PageIndex{3}$显示了如何通过观察斜率和截距来确定线性系统的解数。

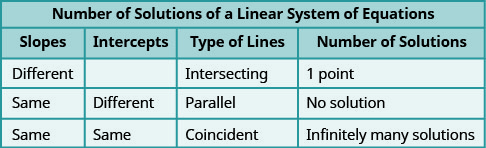
此表标题为 “线性方程组的解数”。共有四列。这些列标有 “斜率”、“截距”、“线路类型”、“解数”。在 “斜率” 下有 “不同”、“相同” 和 “相同”。在 “拦截” 下，第一个单元格为空，然后出现 “不同” 和 “相同” 这两个词。在 “线条类型” 下有 “相交”、“平行” 和 “重合” 等字样。在 “解决方案数量” 下有 “1 分”、“无解” 和 “无限多解”。 — 图$\PageIndex{3}$

让我们再来看看练习中的方程式$\PageIndex{19}$，它为我们提供了平行线。

\ [\ begin {cases} {y=\ frac {1} {2} x−3}\\ {x−2y=4}\ end {cases}\)]

当两条线都采用斜率截距形式时，我们有：

\[y=\frac{1}{2} x-3 \quad y=\frac{1}{2} x-2\]

你知道不可能有单个有序对（x，y）作为这两个方程的解吗？

我们把这样的方程组称为不一致的系统。它没有解决办法。

具有至少一个解的方程组称为一致方程组。

一致和不一致的系统

一致的方程组是具有至少一个解的方程组。

不一致的方程组是没有解的方程组。

我们还通过称方程为独立方程或从属方程来对方程组中的方程进行分类。如果两个方程是独立方程，则每个方程都有自己的解集。相交线和平行线是独立的。

如果两个方程是相关的，则一个方程的所有解也是另一个方程的解。当我们绘制两个依赖方程时，我们会得到重合的线。

独立方程和从属方程

如果两个方程有不同的解，则它们是独立的。

如果一个方程的所有解也是另一个方程的解，则两个方程是相关的。

让我们通过查看三种类型的系统的图表来总结一下。参见图$\PageIndex{4}$和图$\PageIndex{5}$。

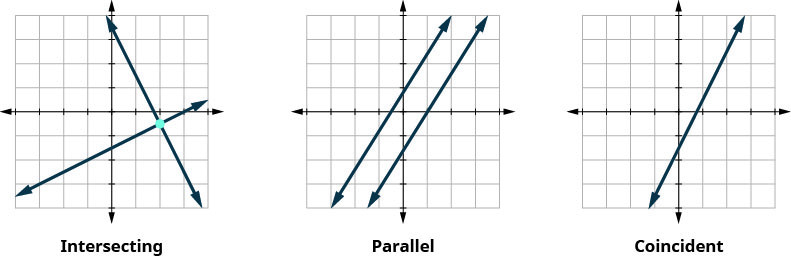
此图在水平行中显示了三个 x y 坐标平面。第一个显示两条相交的直线。第二个显示了两条平行线。第三条显示了两条重合的线。 — 图$\PageIndex{4}$

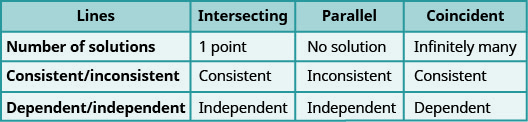
此表有四列和四行。这些列被标记为 “直线”、“相交”、“平行” 和 “重合”。在标有 “行” 列的第一行中，它显示为 “解数”。反过来看，它告诉我们相交线包含 1 个点，一条平行线不提供解，重合线有无限多的解。一致/不一致的线如果相交，则具有一致的线；如果直线平行，则线不一致；如果线重合，则线一致。最后，如果直线相交，则从属线和独立线被视为独立；如果直线平行，则它们也是独立的；如果两条线重合，则从属线。 — 图$\PageIndex{5}$

练习$\PageIndex{25}$

在不绘制图表的情况下，确定解的数量，然后对方程组进行分类：$\begin{cases}{y=3x−1} \\ {6x−2y=12}\end{cases}$

回答

$\begin{array}{lrrl} \text{We will compare the slopes and intercepts} & \begin{cases}{y=3x−1} \\ {6x−2y=12}\end{cases} \\ \text{of the two lines.} \\ \text{The first equation is already in} \\ \text{slope-intercept form.} \\ & {y = 3x - 1}\\ \text{Write the second equation in} \\ \text{slope–intercept form.} \\ & 6x-2y &=&12 \\ & -2y &=& -6x - 12 \\ &\frac{-2y}{-2} &=& \frac{-6x + 12}{-2}\\ &y&=&3x-6\\\\ \text{Find the slope and intercept of each line.} & y = 3x-1 & y=3x-6 \\ &m = 3 & m = 3 \\&b=-1 &b=-6 \\ \text{Since the slopes are the same andy-intercepts} \\ \text{are different, the lines are parallel.}\end{array}$

图形为平行线的方程组没有解，不一致且独立。

练习$\PageIndex{26}$

在不绘制图表的情况下，确定解的数量，然后对方程组进行分类。

$\begin{cases}{y=−2x−4} \\ {4x+2y=9}\end{cases}$

回答: 没有解决方案，不一致，独立

练习$\PageIndex{27}$

在不绘制图表的情况下，确定解的数量，然后对方程组进行分类。

$\begin{cases}{y=\frac{1}{3}x−5} \\ {x-3y=6}\end{cases}$

回答: 没有解决方案，不一致，独立

练习$\PageIndex{28}$

在不绘制图表的情况下，确定解的数量，然后对方程组进行分类：$\begin{cases}{2x+y=−3} \\ {x−5y=5}\end{cases}$

回答

$\begin{array}{lrrlrl} \text{We will compare the slopes and intercepts} & \begin{cases}{2x+y=-3} \\ {x−5y=5}\end{cases} \\ \text{of the two lines.} \\ \text{Write the second equation in} \\ \text{slope–intercept form.} \\ &2x+y&=&-3 & x−5y&=&5\\ & y &=& -2x -3 & -5y &=&-x+5 \\ &&&&\frac{-5y}{-5} &=& \frac{-x + 5}{-5}\\ &&&&y&=&\frac{1}{5}x-1\\\\ \text{Find the slope and intercept of each line.} & y &=& -2x-3 & y&=&\frac{1}{5}x-1 \\ &m &=& -2 & m &=& \frac{1}{5} \\&b&=&-3 &b&=&-1 \\ \text{Since the slopes are the same andy-intercepts} \\ \text{are different, the lines are parallel.}\end{array}$

图形相交的方程组有 1 个解，并且是一致且独立的。

练习$\PageIndex{29}$

在不绘制图表的情况下，确定解的数量，然后对方程组进行分类。

$\begin{cases}{3x+2y=2} \\ {2x+y=1}\end{cases}$

回答: 一种解决方案，一致、独立

练习$\PageIndex{30}$

在不绘制图表的情况下，确定解的数量，然后对方程组进行分类。

$\begin{cases}{x+4y=12} \\ {−x+y=3}\end{cases}$

回答: 一种解决方案，一致、独立

练习$\PageIndex{31}$

在不绘制图表的情况下，确定解的数量，然后对方程组进行分类。 $\begin{cases}{3x−2y=4} \\ {y=\frac{3}{2}x−2}\end{cases}$

回答

$\begin{array}{lrrlrl} \text{We will compare the slopes and intercepts of the two lines.}& \begin{cases}{3x−2y} &=&{4} \\ {y}&=&{\frac{3}{2}x−2}\end{cases} \\ \text{Write the second equation in} \\ \text{slope–intercept form.} \\ &3x-2y&=&4 \\ & -2y &=& -3x +4 \\ &\frac{-2y}{-2} &=& \frac{-3x + 4}{-2}\\ &y&=&\frac{3}{2}x-2\\\\ \text{Find the slope and intercept of each line.} &y&=&\frac{3}{2}x-2\\ \text{Since the equations are the same, they have the same slope} \\ \text{and samey-intercept and so the lines are coincident.}\end{array}$

图形为重合线的方程组具有无限多的解，并且是一致和依赖的。

练习$\PageIndex{32}$

在不绘制图表的情况下，确定解的数量，然后对方程组进行分类。

$\begin{cases}{4x−5y=20} \\ {y=\frac{4}{5}x−4}\end{cases}$

回答: 无限多的解决方案，一致，依赖

练习$\PageIndex{33}$

在不绘制图表的情况下，确定解的数量，然后对方程组进行分类。

$\begin{cases}{ −2x−4y=8} \\ {y=−\frac{1}{2}x−2}\end{cases}$

回答: 无限多的解决方案，一致，依赖

通过绘图求解方程组的应用

我们将使用与数学模型中使用的相同问题求解策略来设置和求解线性方程组的应用程序。我们将在这里稍微修改策略，使其适用于方程组。

对线性方程组使用问题解决策略。

阅读问题。确保所有文字和想法都被理解。
确定我们在寻找什么。
说出我们要找的东西。选择变量来表示这些数量。
转换为方程组。
使用良好的代数技术求解方程组。
检查问题中的答案并确保答案合理。
用完整的句子@@ 回答问题。

在第 5 步中，我们将使用本节中介绍的方法。我们将绘制方程图并找到解。

练习$\PageIndex{34}$

桑德拉正在用果汁和苏打水制成 10 夸脱的冲击力。夸脱的果汁数量是苏打水夸脱数量的 4 倍。桑德拉需要多少夸脱的果汁和多少夸脱的苏打水？

回答

第 1 步。 阅读问题。

第 2 步。 确定我们在寻找什么。

我们正在寻找桑德拉需要多少夸脱的果汁和多少夸脱的苏打水。

第 3 步。 说出我们要找的东西。选择变量来表示这些数量。

让 f = 果汁的夸脱数。
c= 苏打水的夸脱数量

第 4 步。转换为方程组。

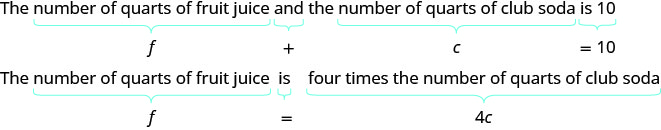
$此图显示了转换为方程的句子。第一句话是：“夸脱果汁的数量和夸脱的苏打水的数量为10。 “夸脱的果汁数” 在短语下方包含一个大括号，方括号下方有一个 “f”。 “And” 的下方还包含一个大括号，并在其下方有一个加号。 “夸脱的苏打水数量” 包含一个大括号，其下方有变量 “c”。最后，短语 “是 10” 包含一个大括号。在此之下，它读起来等于 10。第二句话是：“夸脱果汁的数量是苏打水夸脱数量的四倍”。这句话的设置类似，因为每个短语的下方都有一个大括号。变量 “f” 表示 “夸脱果汁的数量”。等号代表 “是”，“4c” 代表夸脱苏打水数量的四倍。”$

我们现在有了系统。 $\begin{cases}{ f+c=10} \\ {f=4c}\end{cases}$

第 5 步。使用良好的代数技术求解方程组。

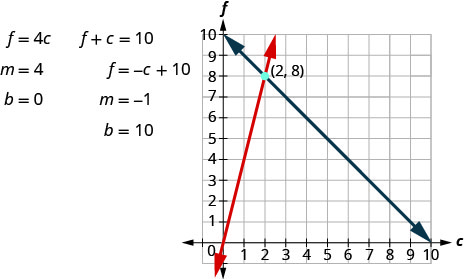
$此图显示了两个方程及其图形。第一个方程为 f = 4c，其中 b = 4，b = 0。第二个方程是 f + c = 10.f = 负 c +10 其中 b = 负 1，b = 10。 x y 坐标平面显示了这两条在 (2, 8) 处相交的直线的图形。$

交点 (2, 8) 是解。这意味着桑德拉需要 2 夸脱的苏打水和 8 夸脱的果汁。

第 6 步。 检查问题中的答案并确保答案合理。

这在问题中有意义吗？

是的，果汁的夸脱数量，8 是苏打水夸脱数量的 4 倍，2。

是的，10 夸脱的拳头是 8 夸脱的果汁加上 2 夸脱的苏打水。

第 7 步。用完整的句子回答问题。

桑德拉需要 8 夸脱的果汁和 2 夸脱的苏打水。

练习$\PageIndex{35}$

曼尼正在用浓缩液和水制成 12 夸脱的橙汁。夸脱水的数量是浓缩液夸脱数量的 3 倍。曼尼需要多少夸脱的浓缩液和多少夸脱的水？

回答: 曼尼需要 3 夸脱的浓缩果汁和 9 夸脱的水。

练习$\PageIndex{36}$

Alisha 正在制作一款 18 盎司的咖啡饮料，由冲泡的咖啡和牛奶制成。冲泡咖啡的盎司数量是盎司牛奶数量的5倍。 Alisha 需要多少盎司的咖啡和多少盎司的牛奶？

回答: 艾丽莎需要 15 盎司的咖啡和 3 盎司的牛奶。

注意

访问这些在线资源，获取有关通过图形求解方程组的更多指导和练习。

关键概念

通过绘图求解线性方程组
1. 绘制第一个方程的图形。
2. 在同一个直角坐标系上绘制第二个方程的图形。
3. 确定两条线是相交、平行还是同一条线。
4. 确定系统的解决方案。
  如果两条线相交，请确定交点。检查以确保它是两个方程的解。这是系统的解决方案。
  如果线是平行的，则系统没有解决方案。
  如果两条线相同，则系统有无限数量的解。
5. 检查两个方程中的解。
从线性系统的图中确定解的数量
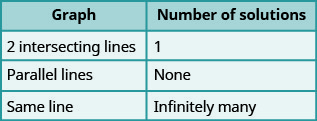
$此表有两列和四行。第一行将每列标记为 “图形” 和 “解数”。 “图形” 下有 “2 条相交线”、“平行线” 和 “同一条线”。在 “解数” 下有 “1”、“无” 和 “无限多”。$
通过查看斜率和截距来确定线性系统的解数
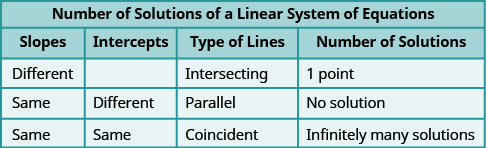
$此表标题为 “线性方程组的解数”。共有四列。这些列标有 “斜率”、“截距”、“线路类型”、“解数”。在 “斜率” 下有 “不同”、“相同” 和 “相同”。在 “拦截” 下，第一个单元格为空，然后出现 “不同” 和 “相同” 这两个词。在 “线条类型” 下有 “相交”、“平行” 和 “重合” 等字样。在 “解决方案数量” 下有 “1 分”、“无解” 和 “无限多解”。$
确定解的数量以及如何对方程组进行分类
$此表有四列和四行。这些列被标记为 “直线”、“相交”、“平行” 和 “重合”。在标有 “行” 列的第一行中，它显示为 “解数”。反过来看，它告诉我们相交线包含 1 个点，一条平行线不提供解，重合线有无限多的解。一致/不一致的线如果相交，则具有一致的线；如果直线平行，则线不一致；如果线重合，则线一致。最后，如果直线相交，则从属线和独立线被视为独立；如果直线平行，则它们也是独立的；如果两条线重合，则从属线。$
线性方程组的问题解决策略
1. 阅读问题。确保所有文字和想法都被理解。
2. 确定我们在寻找什么。
3. 说出我们要找的东西。选择变量来表示这些数量。
4. 转换为方程组。
5. 使用良好的代数技术求解方程组。
6. 检查问题中的答案并确保答案合理。
7. 用完整的句子@@ 回答问题。

词汇表

重合线: 重合线是具有相同斜率和相同的 y 截距的线。

一致的系统: 一致的方程组是具有至少一个解的方程组。

依赖方程: 如果一个方程的所有解也是另一个方程的解，则两个方程是相关的。

系统不一致: 不一致的方程组是没有解的方程组。

独立方程: 如果两个方程有不同的解，则它们是独立的。

方程组的解: 方程组的解是使所有方程成真的变量的值。两个线性方程组的解由有序对 (x, y) 表示。

线性方程组: 当两个或多个线性方程组合在一起时，它们形成线性方程组。

求解 y 的第一个方程。找出斜率和 y 截距。求解 y 的第二个方程。找出斜率和 y 截距。	\(\begin{aligned} 3 x+y &=-1 \\ y &=-3 x-1 \\ m &=-3 \\ b &=-1 \\ 2 x+y &=0 \\ y &=-2 x \\ b &=0 \end{aligned}\)
绘制线条图。	$。$
确定交叉点。	两条线在 (−1, 2) 处相交。
检查两个方程中的解。	\(\begin{array}{rllrll}{3x+y}&{=}&{-1} & {2x +y}&{=}&{0}\\{3(-1)+ 2}&{\stackrel{?}{=}}&{-1} &{2(-1)+2}&{\stackrel{?}{=}}&{0} \\ {-1}&{=}&{-1 \checkmark}&{0}&{=}&{0 \checkmark} \end{array}\)
	解是 (−1, 2)。

	$。$
要找到截距，让 x = 0 求解 y，然后让 y = 0 求解 x。	\(\begin{aligned} x+y &=2 \quad x+y=2 \\ 0+y &=2 \quad x+0=2 \\ y &=2 \quad x=2 \end{aligned}\)	$。$
	$。$
要找到截取次数，假设 x = 0 然后让 y = 0。	\ begin {array} {rlr} {x-y} & {=4} & {x-y} & {= 4}\\ {0-y} & {=4} & {x-0} & {=4}\\ {-y} & {=4}\\ {y} & {=4}\\\ {y}\ end {array}	$。$
绘制线条图。	$此图显示了两条直线在 x y 坐标平面上的点 (3, -1) 处的交点。$
确定交叉点。	线在 (3, −1) 处相交。
检查两个方程中的解。	\(\begin{array}{rllrll}{x+y}&{=}&{2} & {x-y}&{=}&{4}\\{3+(-1)}&{\stackrel{?}{=}}&{2} &{3 - (-1)}&{\stackrel{?}{=}}&{4} \\ {2}&{=}&{2 \checkmark}&{4}&{=}&{4 \checkmark} \end{array}\) 解是 (3, −1)。

学习目标

注意

确定有序对是否是方程组的解

定义：线性方程组

定义：方程组的解

练习\(\PageIndex{1}\)

练习\(\PageIndex{2}\)

练习\(\PageIndex{3}\)

通过绘图求解线性方程组

练习\(\PageIndex{4}\): How to Solve a System of Linear Equations by Graphing

练习\(\PageIndex{5}\)

练习\(\PageIndex{6}\)

通过绘图求解线性方程组。

练习\(\PageIndex{7}\)

练习\(\PageIndex{8}\)

练习\(\PageIndex{9}\)

练习\(\PageIndex{10}\)

练习\(\PageIndex{11}\)

练习\(\PageIndex{12}\)

练习\(\PageIndex{13}\)

练习\(\PageIndex{14}\)

练习\(\PageIndex{15}\)

练习\(\PageIndex{16}\)

练习\(\PageIndex{17}\)

练习\(\PageIndex{18}\)

练习\(\PageIndex{19}\)

练习\(\PageIndex{20}\)

练习\(\PageIndex{21}\)

练习\(\PageIndex{22}\)

练习\(\PageIndex{23}\)

练习\(\PageIndex{24}\)

重合线

确定线性系统的解数

一致和不一致的系统

独立方程和从属方程

练习\(\PageIndex{25}\)

练习\(\PageIndex{26}\)

练习\(\PageIndex{27}\)

练习\(\PageIndex{28}\)

练习\(\PageIndex{29}\)

练习\(\PageIndex{30}\)

练习\(\PageIndex{31}\)

练习\(\PageIndex{32}\)

练习\(\PageIndex{33}\)

通过绘图求解方程组的应用

对线性方程组使用问题解决策略。

练习\(\PageIndex{34}\)

练习\(\PageIndex{35}\)

练习\(\PageIndex{36}\)

注意

关键概念

词汇表