2.1:使用等式的减法和加法属性求解方程
- Page ID
- 204659
在本节结束时,您将能够:
- 验证方程的解
- 使用等式的减法和加法属性求解方程
- 求解需要简化的方程
- 转换为方程并求解
- 翻译和解决应用程序
在开始之前,请参加这个准备测验。
- 评估\(x+4\)时间\(x=−3\)。
如果您错过了此问题,请查看练习 1.5.25。 - 评估\(15−y\)时间\(y=−5\)。
如果您错过了此问题,请查看练习 1.5.31。 - 简化\(4(4n+1)−15n\)。
如果你错过了这个问题,请查看练习 1.10.49。 - 翻译成代数 “5 小于 x”。
如果您错过了此问题,请查看练习 1.3.43。
验证方程的解
求解方程就像发现谜题的答案。 求解方程的目的是找出使方程两边都相同的变量的值——这样我们就得出一个真实的陈述。 使方程成真的变量的任何值都称为方程解。 这是拼图的答案!
方程的解是一个变量的值,当它被替换到方程中时,该变量的陈述是真实的。
- 用数字代替方程中的变量。
- 简化方程两边的表达式。
- 确定所得方程是否为真(左侧等于右侧)
- 如果是真的,那么这个数字就是一个解。
- 如果不是,则该数字不是解决方案。
确定\(x = \frac{3}{2}\)是否为的解\(4x−2=2x+1\)。
- 回答
-
由于方程的解是使方程成真的变量的值,因此首先用解的值代替变量。
\(4 x-2=2 x+1\) 
\(4\left(\color{red}\frac{3}{2}\color{black}\right)-2 \stackrel{?}{=} 2\left(\color{red}\frac{3}{2}\color{black}\right)+1\) 乘以。 \(6-2 \stackrel{?}{=} 3+1\) 减去。 \(4=4 \checkmark \) 由于\(x = \frac{3}{2}\)结果为真方程(4 实际上等于 4),\(\frac{3}{2}\)因此是该方程的解\(4x−2=2x+1\)。
\(y = \frac{4}{3}\)有解决方案\(9y+2=6y+3\)吗?
- 回答
-
不
\(y = \frac{7}{5}\)有解决方案\(5y+3=10y-4\)吗?
- 回答
-
是的
使用等式的减法和加法属性求解方程
我们将使用模型来阐明求解方程的过程。 信封代表变量(因为其内容未知),每个计数器代表一个。 我们将在工作空间中设置一个信封和一些计数器,如图所示\(\PageIndex{1}\)。 工作区的两侧有相同数量的计数器,但有些计数器在信封中 “隐藏”。 你能分辨出信封里有多少柜台吗?
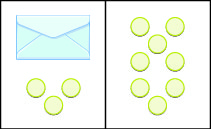
你在想什么? 你在想什么步骤来弄清楚信封里有多少柜台?
也许你在想:“我需要移除左下角的 3 个计数器才能自己拿到信封。 左边的 3 个计数器可以和右边的 3 个计数器配对,所以我可以把它们从两边拿走。 这样右边就剩下了五个计数器,所以信封里必须有 5 个计数器。” 有关此过程\(\PageIndex{2}\)的示意图,请参见图。
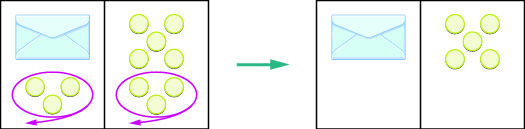
哪种代数方程可以匹配这种情况? 在图中,工作空间的\(\PageIndex{3}\)每一侧代表一个表达式,中心线取代等号。 我们将信封的内容称为 x。
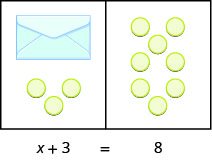
让我们用代数写下我们为发现信封中有多少计数器而采取的步骤:
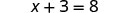 |
|
| 首先,我们从两边拿走了三个。 |  |
| 然后我们只剩下五个。 | 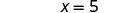 |
查看:
信封里有五个再加上三个等于八个!
\[5+3=8\]
我们的模型让我们了解了我们需要做些什么来求解一种方程。 目标是将变量本身隔离在方程的一侧。 为了用数学方法求解此类方程,我们使用等式的减法属性。
对于任何数字 a、b 和 c,
\[\begin{array} {ll} {\text{If}} &{a = b} \\ {\text{then}} &{a - c = b - c} \end{array}\]
当你从方程的两边减去相同的量时,你仍然相等。
进行操纵数学活动 “等式的减法属性” 将有助于你更好地了解如何使用等式的减法属性求解方程。
让我们看看如何使用这个属性来求解方程。 请记住,目标是隔离方程一侧的变量。 然后我们通过将值代入方程来检查我们的解,以确保我们有真实的陈述。
解决:\(y+37=−13\)。
- 回答
-
为了单独获得 y,我们将使用相等的减法属性撤消 37 的加法。

每边减去 37 以 “撤消” 加法。 
简化。 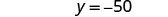
查看: 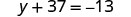
替代\(y=−50\) 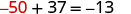
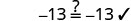
由于 y=−50 使 y+37=−13 成为一个真实的陈述,所以我们有了这个方程的解。
解决:\(x+19=−27\)。
- 回答
-
\(x=−46\)
解决:\(x+16=−34\)。
- 回答
-
\(x=−50\)
当方程从变量中减去一个数字时会发生什么,就像在方程中一样\(x−5=8\)? 我们使用方程的另一个属性来求解从变量中减去一个数字的方程式。 我们想隔离变量,所以为了 “撤消” 减法,我们将把数字加到两边。 我们使用平等的加法属性。
对于任何数字 a、b 和 c,
\[\begin{array} {ll} {\text{If}} &{a = b} \\ {\text{then}} &{a + c = b + c} \end{array}\]
当你从方程的两边加上相同的量时,你仍然相等。
在练习中\(\PageIndex{4}\),将 37 添加到 y 中,因此我们减去 37 以 “撤消” 加法。 在练习中\(\PageIndex{7}\),我们需要使用相等的加法属性 “撤消” 减法。
解决:\(a−28=−37\)。
- 回答
-

每边加 28 即可 “撤消” 减法。 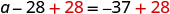
简化。 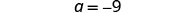
查看: 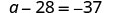
替代\(a=−9\) 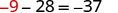
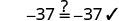
解决的办法\(a−28=−37\)是\(a=−9\)。
解决:\(n−61=−75\)。
- 回答
-
\(n=−14\)
解决:\(p−41=−73\)。
- 回答
-
\(p=−32\)
解决:\(x - \frac{5}{8} = \frac{3}{4}\)
- 回答
-
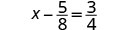
使用等式的加法属性。 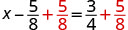
找到 LCD 添加右边的分数。 \(x-\frac{5}{8}+\frac{5}{8}=\frac{6}{8}+\frac{5}{8}\) 简化。 \(x=\frac{11}{8}\) 查看: 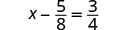
替代\(x= \frac{11}{8}\) 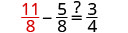
减去。 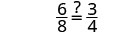
简化。 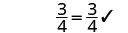
解决的办法\(x - \frac{5}{8} = \frac{3}{4}\)是\(x= \frac{11}{8}\)。
解决:\(p−\frac{2}{3}=\frac{5}{6}\)。
- 回答
-
\(p = \frac{9}{6} p =\frac{3}{2}\)
解决:\(q−\frac{1}{2}=\frac{5}{6}\)。
- 回答
-
\(q =\frac{4}{3}\)
下一个例子将是一个带小数的方程。
解决:\(n−0.63=−4.2\)。
- 回答
-
\(n-0.63=-4.2\) 使用等式的加法属性。 
添加。 \(n=-3.57\) 查看: \(n=-3.57\) 让\(n=−3.57\)。 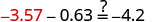
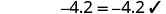
解决:\(b−0.47=−2.1\)。
- 回答
-
\(b=−1.63\)
解决:\(c−0.93=−4.6\)。
- 回答
-
\(c=−3.67\)
求解需要简化的方程
在前面的示例中,我们仅通过一次操作就能隔离变量。 我们在代数中遇到的大多数方程都需要更多的步骤才能求解。 通常,在使用等式的减法或加法属性之前,我们需要简化方程的一边或两边。
在尝试隔离变量之前,应始终尽可能简化。 请记住,简化表达式意味着要完成表达式中的所有操作。 一次简化方程的一面。 请注意,简化与用于求解方程的过程不同,在该方程中,我们对两边都应用运算。
解决:\(9x−5−8x−6=7\)。
- 回答
-




解决:\(8y−4−7y−7=4\)。
- 回答
-
\(y=15\)
解决:\(6z+5−5z−4=3\)。
- 回答
-
\(z=2\)
求解:5 (n−4) −4n=−8。
- 回答
-
在尝试隔离变量之前,我们尽可能简化方程的两边。
\(5(n-4)-4 n=-8\)
在左边分布。 \(5 n-20-4 n=-8\) 使用交换属性重新排列术语。 \(5 n-4 n-20=-8\) 将相似的术语组合在一起。 \(n-20=-8\) 每一面都尽可能简化。 接下来,分离 n。 使用等式的加法属性撤消减法。 \(n-20 \; \color{red}{+ 20} \;\color{black}{=-8}\; \color{red}{+20}\) 添加。 \(n=12\) 查看。 替代 n=12。
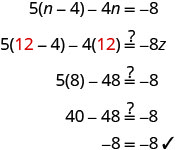
解决的办法\(5(n−4)−4n=−8\)是\(n=12\)。
解决:\(5(p−3)−4p=−10\)。
- 回答
-
\(p=5\)
解决:\(4(q+2)−3q=−8\)。
- 回答
-
\(q=−16\)
解决:\(3(2y−1)−5y=2(y+1)−2(y+3)\)。
- 回答
-
在分离变量之前,我们简化了方程的两边。
\(3(2 y-1)-5 y=2(y+1)-2(y+3)\) 在两面分布。 \(6 y-3-5 y=2 y+2-2 y-6\) 使用加法的可交换属性。 \(6 y-5 y-3=2 y-2 y+2-6\) 将相似的术语组合在一起。 \(y-3=-4\) 每一面都尽可能简化。 接下来,隔离 y。 使用等式的加法属性撤消减法。 \(y-3 \color{red} + 3 \color{black} = -4 \color{red} +3\) 添加。 \(y=-1\) 查看。 让 y=−1。
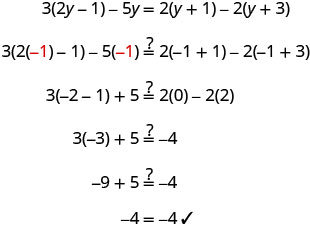
解决的办法\(3(2y−1)−5y=2(y+1)−2(y+3)3(2y−1)−5y=2(y+1)−2(y+3)\)是\(y=−1\)。
解决:\(4(2h−3)−7h=6(h−2)−6(h−1)\)。
- 回答
-
\(h = 6\)
解决:\(2(5x+2)−9x=3(x−2)−3(x−4)\)。
- 回答
-
\(x=2\)
转换为方程并求解
为了用代数求解应用程序,我们将首先从英语句子翻译成方程式。 我们的第一步是寻找可以转换为等号的单词(或多个单词)。 以下是一些常用的单词。
等于 =
- 是
- 等于
- 等同于
- 结果是
- 给
- 是
- 将是
下面列出了我们用来将句子翻译成方程的步骤。
- 找到 “等于” 字。 转换为等号 (=)。
- 将 “等于” 字左边的单词翻译成代数表达式。
- 将 “等于” 字右边的单词翻译成代数表达式。
平移并求解:比 x 多十一个等于 54。
- 回答
-
翻译。 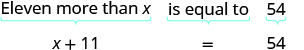
从两边减去 11。 
简化。 
查看:54 Eleven 比 43 多吗?
\[\begin{array} {rrr} {43 + 11} &{\stackrel{?}{=}} &{54}\\ {54} &{=} &{54\checkmark} \end{array}\]
平移并求解:比 x 多十等于 41。
- 回答
-
\(x+10=41;x=31\)
平移并求解:小于 x 的十二等于 51。
- 回答
-
y−12=51;y=63
翻译并求解:12t 和 11t 的差值为 −14。
- 回答
-
翻译。 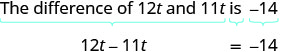
简化。 
查看:
\[\begin{array} {rrl} {12(-14) - 11(-14)} &{\stackrel{?}{=}} &{-14}\\{-168 + 154} &{\stackrel{?}{=}} &{-14} \\ {-14} &{=} &{-14\checkmark}\end{array}\]
翻译并求解:4x 和 3x 的差异为 14。
- 回答
-
\(4x−3x=14;x=14\)
翻译并求解:7a 和 6a 的差值为 −8。
- 回答
-
\(7a−6a=−8;a=−8\)
翻译和解析应用程序
大多数情况下,需要代数解的问题来自现实生活中的问题。 首先,这个问题是用英语(或提问者的语言)提出的,而不是用数学符号提出的。 因此,能够将日常情况翻译成代数语言是一项重要的技能。
首先,我们将用一句话重述问题,分配一个变量,然后将句子转换为要解的方程。 在分配变量时,请选择一个能提醒你要找的东西的字母。 例如,如果你要解决一个关于硬币的问题,你可以使用 q 来表示季度数。
麦金太尔家族回收了两个月的报纸。 两个月的报纸总重达57磅。 第二个月,报纸重达28磅。 第一个月报纸的重量是多少?
- 回答
-







翻译成代数方程并求解:
帕帕斯家族有两只猫,宙斯和雅典娜。 它们加起来重 23 磅。 宙斯重 16 磅。 雅典娜重多少?
- 回答
-
7 磅
翻译成代数方程并求解:
山姆和亨利是室友。 他们总共有 68 本书。 山姆有 26 本书。 亨利有多少本书?
- 回答
-
42 本书
- 阅读问题。 确保所有文字和想法都被理解。
- 确定我们在寻找什么。
- 说出我们要找的东西。 选择一个变量来表示该数量。
- 翻译成方程式。 用一句话用重要信息重述问题可能会有所帮助。
- 使用良好的代数技巧求@@ 解方程。
- 检查问题中的答案并确保答案合理。
- 用完整的句子@@ 回答问题。
兰德尔花了28,675美元购买了他的新车。 这比标价低了875美元。 这辆车的标价是多少?
- 回答
-
\(\begin{array} {ll} {\textbf {Step 1. Read}\text{ the problem. }} &{}\\\\ {\textbf {Step 2. Identify}\text{ what we are looking for.}} &{\text{"What was the sticker price of the car?"}} \\\\ {\textbf{Step 3. Name}\text{ what we are looking for.}} &{} \\ {\text{Choose a variable to represent that quantity.}} &{\text{Let s = the sticker price of the car.}} \\\\{\textbf {Step 4. Translate}\text{ into an equation. Restate }} &{} \\ {\text{the problem in one sentence.}} &{$\text{28675 is } $\text{875 less than the sticker price}} \\ \\ {} &{$\text{28675 is } $\text{875 less than s}}\\ {}&{28675 = s - 875} \\ {\textbf {Step 5. Solve}\text{ the equation. }} &{28675 + 875 = s - 875 + 875}\\ {} &{29550 = s} \\ \\ {\textbf {Step 6. Check}\text{ the answer. }} &{} \\ {\text{Is }$875\text{ less than }$29550\text{ equal to } $28675?} &{} \\ {29550 - 875 \stackrel{?}{=} 28675} &{} \\ {28675 = 28675\checkmark} &{} \\ \\ {\textbf {Step 7. Answer}\text{ the question with }} &{\text{The sticker price of the car was }$29550.} \\ {\text{a complete sentence.}} &{} \end{array}\)
翻译成代数方程并求解:
埃迪花了19875美元买了他的新车。 这比标价低了1025美元。 这辆车的标价是多少?
- 回答
-
20900 美元
翻译成代数方程并求解:
白天电影的入场价为7.75美元。 这比晚上的价格少了3.25美元。 这部电影晚上要花多少钱?
- 回答
-
11.00 美元
关键概念
- 确定一个数字是否是方程的解
- 用数字代替方程中的变量。
- 简化方程两边的表达式。
- 确定生成的陈述是否正确。
- 如果是真的,那么这个数字就是一个解。
- 如果不是,则该数字不是解决方案。
- 平等的加法属性
- 对于任何数字 a、b 和 c,如果 a=b,则 a+c=b+c。
- 相等的减法属性
- 对于任何数字 a、b 和 c,如果 a=b,则 a−c=b−c。
- 将句子翻译成方程式
- 找到 “等于” 字。 转换为等号 (=)。
- 将 “等于” 字左边的单词翻译成代数表达式。
- 将 “等于” 字右边的单词翻译成代数表达式。
- 解决应用程序
- 阅读问题。 确保所有文字和想法都被理解。
- 确定我们在寻找什么。
- 说出我们要找的东西。 选择一个变量来表示该数量。
- 翻译成方程式。 用一句话用重要信息重述问题可能会有所帮助。
- 使用良好的代数技巧求解方程。
- 检查问题中的答案并确保答案合理。
- 用完整的句子回答问题。
词汇表
- 方程的解
- 方程的解是一个变量的值,当它被替换到方程中时,该变量的陈述是真实的。


