Skip to main content
Global

4.12: 应用函数示例

  1. Last updated
  2. Save as PDF
  • Page ID
    171244

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    函数的应用示例（又名单词问题！） 可以采取多种形式。

    准备好使用本章中回顾过的任何类型的函数。

    示例 Template:Index

    如果工人工作超过40个小时，暑期工作会为加班支付半工资。 40 小时后，工人的工资是每小时工资\($12.00\)的 1.5 倍。

    1. 编写并绘制一个分段函数，根据工作时数给出每周工资 P。提示：这可能很棘手，想想如何表示超过 40 小时的小时数。
    2. 工作 45 小时能赚多少钱？
    解决方案
    1. 要编写分段函数，请执行以下操作：

    \(P (h) = \left\{\begin{array}{cc} 12h &0 < h \leq 40 \\ 12(40) + 1.5(12)(h − 40) &h > 40\end{array} \right.\)

    要绘制此函数的图表，请制作解决方案表：

    的解决方案表\(P (h) = 12h \)

    域名\(0 < h \leq 40\)
    \(h\) \(P(h)\)
    1 \($12.00\)
    10 \($120.00\)
    40 \($480.00\)

    的解决方案表\(P (h) = 12(40) + 1.5(7)(h − 40) \)

    简化\(P (h) = 18h − 240 \)

    域名\(h > 40\)
    \(h\) \(P(h)\)
    41 498
    45 570
    50 660
    60 840
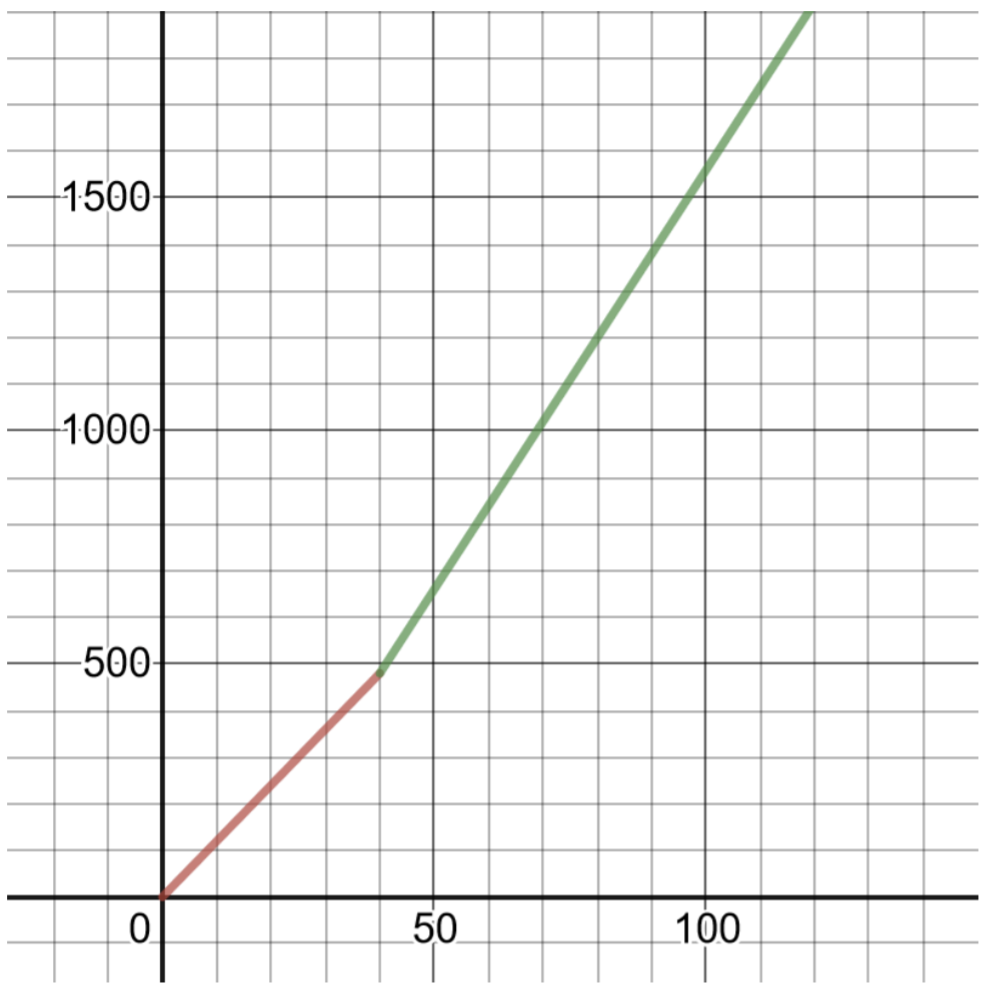
    clipboard_ef0cbdf88861b06f2927739d371a66cd0.png
    图 Template:Index

    1. \($570.00\)工作45小时（参见解决方案表）
    示例 Template:Index

    美国宇航局在\(t=0\)几秒钟内发射火箭。 它的高度，以海拔米为单位，随时间变化，由下式给出\(h(t) = −4.9t^2 + 46t + 227\)。

    1. 假设火箭会飞溅到海里，飞溅会在什么时候发生？
    2. 火箭达到峰值时海拔多高？
    解决方案
    1. 在 splash down 时\(h(t) = 0\)，将函数设置为 0 并求解\(t\)。

    \(0 = −4.9t 2 + 46t + 227\)

    使用二次公式求解这个方程，用\(a = −4.9\)、\(b = 46\)、\(c = 227\)

    \(\begin{aligned} t &= \dfrac{−46 \pm \sqrt{46^2 − 4(−4.9)(227) }}{2(−4.9) } && \text{Quadratic Formula} \\ t &= \dfrac{−46 \pm \sqrt{ 2116 + 4449.2 }}{−9.8 } &&\text{Simplify the radical} \\ t &= \dfrac{46 \pm \sqrt{ 6565.2 }}{9.8 } &&\text{Further simplify the radical, divide all terms by -1 (still have } \pm\text{ )} \\t &= \dfrac{46 \pm 81.026 }{9.8 } &&\text{Square root} \\ t &= \dfrac{46 + 81.026 }{9.8 } &&\text{Addition} \\ t &= \dfrac{46 − 81.026 }{9.8} && \text{Subtraction} \\ t& = 12.96 \text{ and } t = −3.57&& \text{Two solutions, reject negative solution because time cannot be negative} \\ t &= 12.96 \text{ seconds }&&\text{Final Answer} \end{aligned}\)

    1. 火箭达到峰值时海拔多高？

    二次函数前导项系数的符号\(h(t) = −4.9t^2 + 46t + 227\)显示抛物线的开口方向。 系数为\(−4.9\)，由于系数为负，二次函数向下打开。

    现在我们需要找到顶点。 顶点有序对的 y 值将显示范围的起点。

    顶点是\(\left(− \dfrac{b }{2a} , f\left( −\dfrac{ b }{2a}\right) \right)\)，\(a = −4.9\)和\(b = 46\)

    顶点是\(\left(−\dfrac{ 46 }{2(−4.9) }, f\left( − \dfrac{46 }{2(−4.9)}\right)\right)\)

    顶点是\((4.694, f (4.694))\)哪个是\((4.694, (−4.9)(4.694)^2 + (46)(4.694) + 227 ))\)或\((4.694, 334.959)\)

    火箭在其峰值的高度高于海平面数\(334.959\)米。

    示例 Template:Index

    为了促进阿拉斯加游轮的团体销售，旅行社将团体中每个\($5\)人的常规票价降低了\($4500\) by。

    1. 写一个线性方程式，如果\(p\)人们成群旅行\(f(p)\)，则给出每人成本。
    2. 使用方程式确定 50 人的成本。
    解决方案
    1. 由于每人成本的减少幅度相同，因此这是一个线性方程式。

    使用\(f(x) = mx + b\)，或者让我们把它写成\(f(p) = mp + b\)，按\(f(p)\)人均费用计算。

    \(f(p) = mp + b\)

    由于小组中每人的每人费用减少了5美元，这就是线的斜率。

    \(\begin{aligned} f(p)&= −5p + b && \text{Slope-intercept form of the equation of a line} \\ f(p) &= −5p + 4500 &&\text{The y-intercept is the starting point, so the regular ticket price of }$4500 {is the y-intercept} \\ f(p)& = −5p + 4500 && \text{Linear Equation} \end{aligned}\)

    1. 使用方程式确定 50 人的成本。

    \(\begin{aligned} f(50) &= −5(50) + 4500 && \text{Replace p with 50 people in the Linear Equation} \\ f(50) &= −250 + 4500 &&\text{Simplify} \\ f(50) &= 4250 &&\text{Simplify} \\ \text{If }50 &\text{ people take the cruise, the cost per-person for the cruise is } $4250&&\text{Final Answer }\end{aligned}\)

    练习 Template:Index

    完成以下应用函数问题：

    1. 裁缝要在夹克背面缝上运动员的名字，则\($5\)每封信收取\($20\)加价的基本费用。
      1. 写一个线性方程式，找出在夹克背面缝上包含 x 个字母的名字的成本。
      2. 一个包含 11 个字母的名字的费用是多少？
    2. 在墨西哥阿卡普尔科，一个受欢迎的旅游胜地是观看男子从悬崖潜入75英尺以下的水域。 潜水员在潜水\(t\)几秒钟后在水\(f(t)\)面之上的身高（以英尺为单位）由下式给出\(f(t) = −16t^2+75\)。
      • 潜水持续多长时间？
    3. 在某个国家，所得税的评估方式如下：最高不征收所得税\($15000\)。 超过\($15000\)的收入按以下税\($30000\)率征税\(12%\)。 超过的收入\($30000\)按以下税率征税\(18%\)。
      1. 写下上述信息的分段函数并绘制其图形。
      2. 确定对收入应缴纳的税额\($18000\)。