Skip to main content
Global

4.11: 分段定义函数

  1. Last updated
  2. Save as PDF
  • Page ID
    171162

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    定义：分段定义函数

    分段定义函数是使用不同方程为域的不同部分定义的函数。

    示例 Template:Index

    计算以下分段定义函数的给定值\(x\)，然后绘制函数的图形：

    \(f(x) = \left\{\begin{array}{cc}−2x + 1 & −1 \leq x < 0 \\ x^2 + 2 &0 \leq x \leq 2\end{array} \right.\)

    解决方案

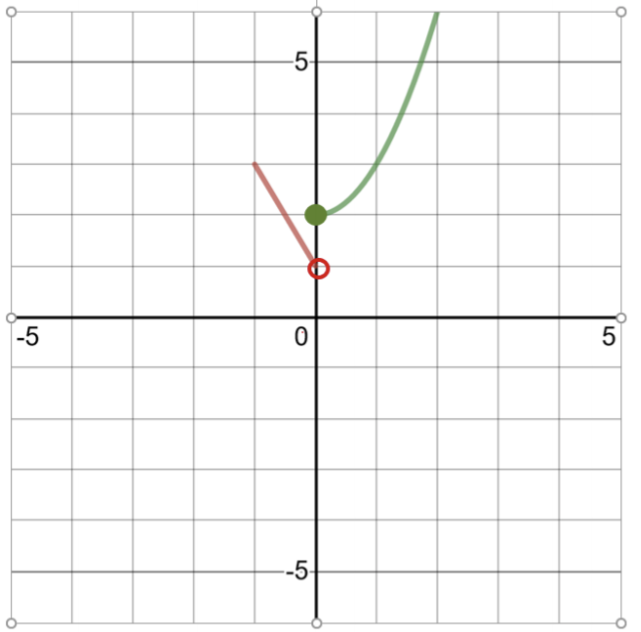
    要绘制此函数的图表，请制作解决方案表：

    的解决方案表\(f(x) = −2x + 1 \)

    域名\(−1 \leq x < 0\)
    \(x\) \(f(x)\)
    -1 3
    0 1（在此处打开圆圈，0 不在域中）

    的解决方案表\(f(x) = x^2 + 2\)

    域名\(0 \leq x \leq 2\)
    \(x\) \(f(x)\)
    0 2
    1 3
    2 6
    clipboard_e94fd5197718a7373772af1280306cf06.png
    图 Template:Index
    示例 Template:Index

    计算以下分段定义函数的给定值\(x\)，然后绘制函数的图形：

    \(f(x) = \left\{\begin{array}{cc} −x + 1 &x \leq −1 \\ 2 & −1 < x \leq 1 \\ −x + 3 &x > 1 \end{array}\right.\)

    解决方案

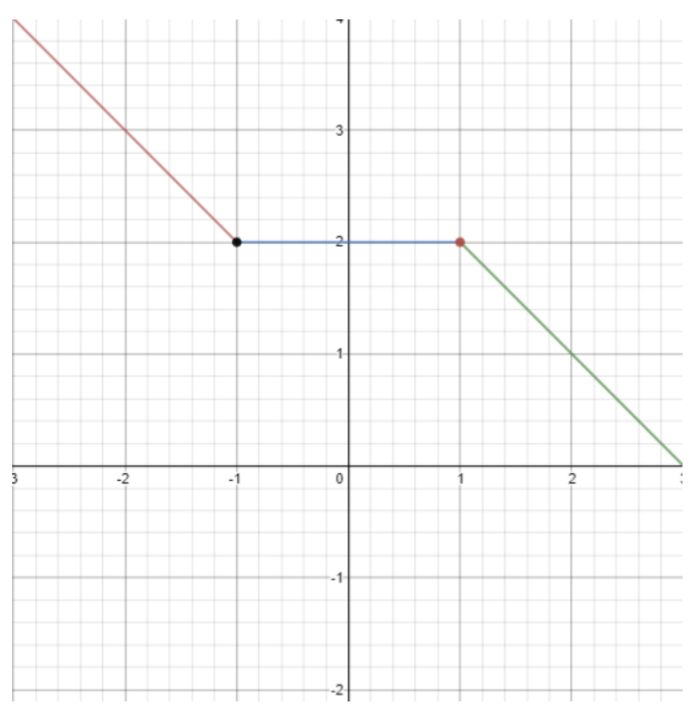
    要绘制此函数的图表，请再次绘制解表：

    的解决方案表\(f(x) = −x + 1\)

    域名\(x \leq −1\)
    \(x\) \(f(x)\)
    -3 4
    -2 3
    -1 2（此处为封闭圆圈，域中为 -1）

    的解决方案表\(f(x) = 2\)

    域名\(−1 < x \leq 1\)
    \(x\) \(f(x)\)
    -1 2（打开由上一个函数填充的圆圈，-1 不在域中）
    0 2
    1 2（此处为闭圈，1 在域中）

    的解决方案表\(f(x) = −x + 3\)

    域名\(x > 1\)
    \(x\) \(f(x)\)
    1 2（打开由上一个函数填充的圆圈，1 不在域中）
    2 1
    3 0
    clipboard_e795cd2fce50083772c8741bdcad72855.png
    图 Template:Index
    练习 Template:Index

    根据 x 的给定值计算以下分段定义的函数，然后绘制函数的图形：。

    1. \ (f (x) =\ 左\ {\ begin {array} {cc}
      x & x<0\\
      2 x+1 &x\ geq 0
      \ end {array}\ 右。\)
    2. \(g(x) = \left\{\begin{array}{cc} 4 − x& x < 2\\ 2x − 2 &x \geq 2 \end{array} \right.\)
    3. \(h(x) = \left\{\begin{array}{cc} −x − 1 & x < −1 \\ 0& −1 \leq x \leq 1 \\ x + 1 & x > 1 \end{array} \right.\)
    4. \(g(x) = \left\{\begin{array}{cc} 6 & −8 \leq x < −4 \\ 3 &−4 \leq x \leq 5 \end{array}\right.\)
    5. \(f(x) = \left\{\begin{array}{cc} −x + 1 & −1 \leq x < 1 \\ \sqrt{x − 1 } &1 \leq x \leq 5\end{array}\right.\)