4.8: 绘制函数(不使用微积分)
- Page ID
- 171199
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)
有一些基本函数,称为工具包函数,学生应该通过函数定义和图表来识别这些函数。 对于其中的每一个函数,\(x\)是输入变量,\(f(x)\)是输出变量。 以下图片出自 Calaway、Hoffman 和 Lippman 的 OER 教科书《商业微积分》,经许可使用(知识共享署名 3.0 美国许可证)。


与传统的 STEM 微积分 I 课程不同,这门商业与社会科学微积分课程不使用函数转换来教授图形函数。
本课的学生需要制作一张解表并绘制函数图表。 学生还将学习如何使用微积分绘制函数图!
绘制以下函数的图表:
- \(f(x) = \sqrt[3]{x}\)
- \(f(x) = \dfrac{1 }{x^2 − 3}\)
解决方案
- 制作一个解表并定义函数的域。
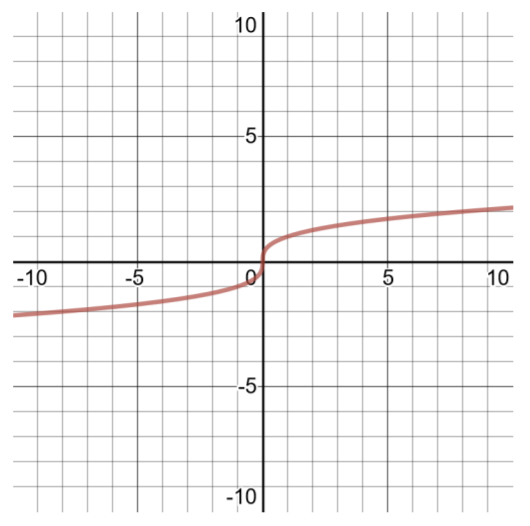
| \(f(x) =\sqrt[3]{x}\)域名解决方案表\((−\infty , \infty )\) | |
| \(x\) | \(f(x)\) |
| -8 | -2 |
| -1 | -1 |
| 0 | 0 |
| 1 | 1 |
| 8 | 2 |
- 制作一个解表并定义函数的域。 要识别这个有理函数的域,请注意分母。 分母不能等于 0。 设置分母 = 0 以求解 x 并找出 x 不允许的值。
\(\begin{aligned} f(x) &= \dfrac{1 }{x^2 − 3}\\ 0 &= x^2 − 3 \\3 &= x^2 \\ \pm \sqrt{3} &=\sqrt{x^2} \\ \pm \sqrt{3}& = x \end{aligned}\)
这些数字需要从此函数的域\(−\sqrt{3}\)(大约 −1.732))和\(\sqrt{3}\)(大约 1.732))中排除。
要正确绘制此函数的图形,重要的是要检查这些被排除在域之外的数字周围的行为。 因此,解表中有这么多有序对的原因。 可以这样想:从的域开始\((−\infty , \infty )\),但必须删除任何会导致问题的数字(比如在本例中,将导致函数分母变为 0 的数字,因为除以 0 是未定义的)。 手工绘制这样的函数非常繁琐,但对于学生来说,要想在商业和社会科学微积分中取得成功,这是一项重要的技能。
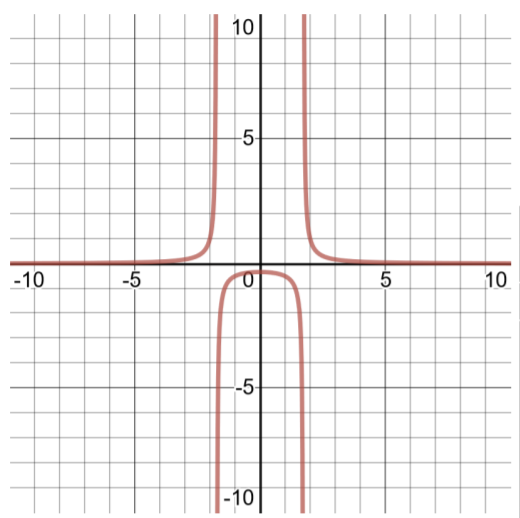
| \(f(x) = \sqrt[3]{ x}\)域名解决方案表\((−\infty , \infty )\) | |
| \(x\) | \(f(x)\) |
| -4 | 0.077 |
| -3 | 0.167 |
| -2 | 1 |
| -1.5 | -1.333 |
| -1 | -0.5 |
| -0.5 | -0.364 |
| 0 | 0 |
| 0.5 | -0.364 |
| 1 | -0.5 |
| 1.5 | -1.333 |
| 2 | 1 |
| 3 | 0.167 |
| 4 | 0.077 |
练习问题:绘制以下函数的图形,注意函数的域。
- \(f(x) = 2x^3\)
- \(f(x) = \dfrac{1 }{2x^2}\)
- \(f(x) = 4 \vert x − 2 \vert\)
- \(f(x) = \dfrac{1 }{3} x − 12 \)
- \(f(x) = \dfrac{1 }{x − 7}\)
- \(f(x) = 3\sqrt{2x^3 + 1}\)


