4.6: 多项式函数
- Page ID
- 171213
多项式函数是一种可以用一般形式编写的函数:
\(f(x) = a_n x^n + a_{n−1} x^{n−1 }+ ... + a_1x + a_0\)
对于\(n\)一个非负整数,称为多项式的次数。 系数\(a_0\)、\(a_1\)\(\ldots\)、和是具有前导系数 an 的实数\(a_n \neq 0\)。 多项式函数的域是\((−\infty , \infty )\)。 度数多项式函数的图形最多\(n\)\(n\)可以与 x 轴相交。 这些是多项式函数的根。
本节中没有示例或作业。
二次函数
\(f(x) = ax^2 + bx + c\)哪里\(a\neq 0\)
是标准形式的二次函数,其图形是抛物线。 当前导系数为正时,二次函数的图形向上打开。\(a\) 当前导系数为负时,二次函数的图形向下打开。\(a\)
在直角坐标系\(f(x) = −x^2 + 5x + 3\)中绘制图形。 用代数求出顶点、x 截距和 y 截距。
解决方案
通过\(\left(\dfrac{-b}{2 a}, f\left(\dfrac{-b}{2 a}\right)\right)\)使用\(a = −1\)、\(b = 5\)和计算来找到顶点\(c = 3\)。
\ (\ begin {aligned}
\ 左 (\ dfrac {-b} {2 a},f\ 左 (\ dfrac {-b} {2 a}\ 右) &=&&\ text {找到抛物线的顶点}\
\\ dfrac {2 (-1)} &=\
\ dfrac {5} {2} &=2.5\ text {简化}\\
\ dfrac {-5} {2 (-1)} &=2.5\\
f (2.5) &=-(2.5) ^ {2} +5 (2.5) +3=9.25=&& f\ 左 (\ dfrac {-b} {2 a}\ 右) =9.25\\\ 左 (\ dfrac {-b} {2 a}\ 右) & =( 2.59.25) &&\ text {抛物线顶点}
\ end {对齐}\)
要找到拦截,请执行以下操作:
\ (\ begin {aligned} 0&=-x^ {2} +5 x+3 &&\ text {x-intercept,set} f (x) =0\\ 0&=-x^ {2} +5 x+3 &&\ text {使用二次公式求解这个方程(无法分解)。 让} a=-1、b=5、c=3\\ x&=\ dfrac {-5\ pm\ sqrt {(5) ^ {2} -4 (-1) (3)} {2 (-1)} &&\ text {二次公式
}\\ x&=\ dfrac {-5\
pm\ sqrt {37}} {-2} &&\ text {Simplify}\\ x&= -0.54\ text {或} x=5.54 &&\ text {这个二次函数有两个根(x-intercepts)。}\\ f (0) &=-0^ {2} +5 (0) +3 &&\ text {y-intercept,set} x=0\\ f (0) &=3 &&\ text {y-intercept}\ end {aligned}\)
绘制四个有序对的图表,并在需要时计算更多有序对:\((2.5, 9.25)\)\((−.54, 0)\)、、\((5.54, 0)\)、\((0, 3)\)。

- \(f(x) = 2x ^2 − 5x − 5\)
- \(f(x) = 0.5x ^2 − 6x + 21\)
- \(f(x) = −4x ^2 − 8x − 3\)
- \(f(x) = −4x^ 2 + 16x − 15\)
- \(f(x) = x^ 2 − 8x + 12\)
- \(f(x) = −7x^ 2 + 100x − 10\)
三次和高阶函数
三次函数是三次多项式函数,可以用一般形式编写:
\(f(x) = a_3x^ 3 + a_2x^2 + a_1x + a_0\)
以 3 作为三次函数的度数。 系数\(a_0\)、\(a_1\)\(a_2\)、\(a_3\)是具有前导系数的实数\(a_3 \neq 0\)。 三次函数的域是\((−\infty , \infty )\)。
尽可能进行因子分解,然后通过创建解表来绘制函数的图形:
\(f(x) = x^3 − 4x^2 + 6x − 1\)
解决方案
这个多项式的度数为 3,很难分解。 创建解决方案表以绘制图表。

| 的解决方案表\(f(x) = x^3 − 4x^2 + 6x − 1\) | |
| \(x\) | \(f(x)\) |
| -2 | \(f(−2) = (−2)^3 − 4(−2)^2 + 6(−2) − 1 = −37\) |
| -1 | \(f(−1) = (−1)^3 − 4(−1)^2 + 6(−1) − 1 = −12\) |
| 0 | \(f(0) = (0)^3 − 4(0)^2 + 6(0) − 1 = −1\) |
| 1 | \(f(1) = (1)^3 − 4(1)^2 + 6(1) − 1 = 2\) |
| 2 | \(f(2) = (2)^3 − 4(2)^2 + 6(2) − 1 = 3\) |
尽可能进行因子分解,然后通过创建解表来绘制函数的图形:
\(g(x)=x^4-16\)
解决方案
这个多项式的度数为 4,并且由于它是平方差,因此可以将其分解为二项式的乘积来找到多项式的零。 创建解决方案表以绘制图表。
\(\begin{aligned} g(x)&=\left(x^{2}-4\right)\left(x^{2}+4\right) && \text{Factoring into the sum and difference of binomials.} \\ g(x)&=(x-2)(x+2)\left(x^{2}+4\right) && \text{Further factoring. Set each binomial equal to zero to find the real number zeroes of the polynomial.} \\ x-2&=0, x=2 && \text{The first real number zero of the polynomial, }(2,0) \\ x+2&=0, x=-2 &&\text{The second real number zero of the polynomial, } (2,0) \\ x^{2}+4&=0, x^{2}=-4 && \text{The third binomial factor does not produce real number zeroes, } \\ & &&\text{because no number squared can result in a negative value.} \end{aligned}\)
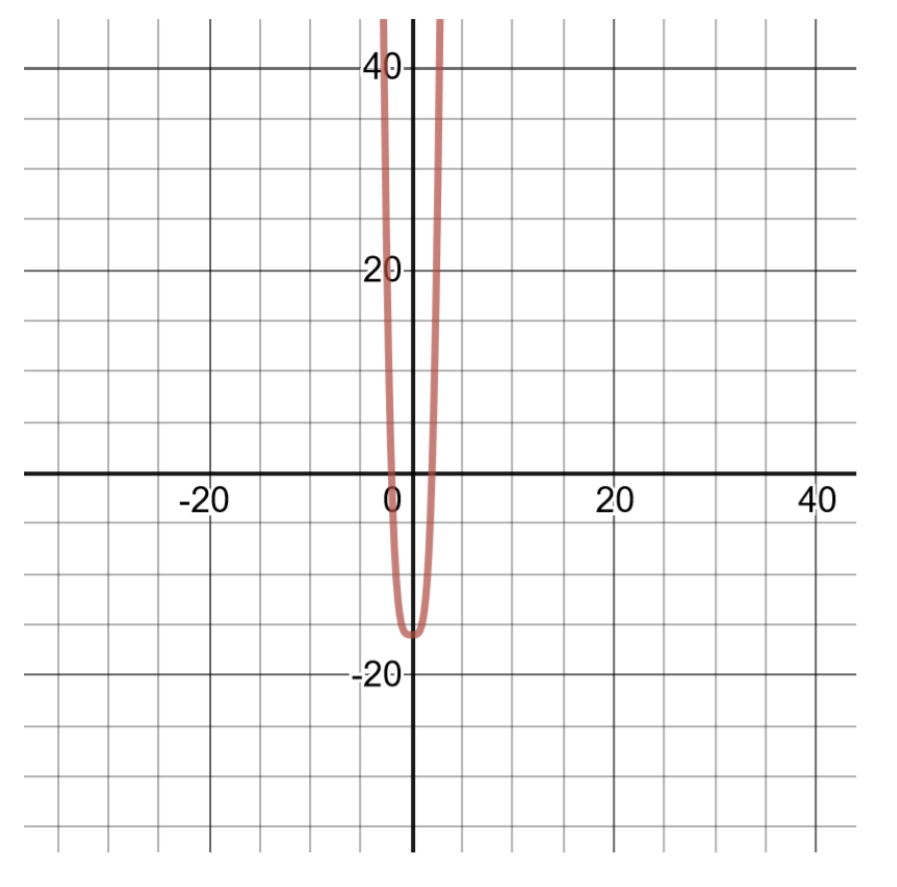
| 的解决方案表\(g(x)=x^4-16\) | |
| \(x\) | \(g(x)\) |
| -2 | \(g(−2) = (−2)^4 − 16 = 16 − 16 = 0\) |
| -1 | \(g(−1) = (−1)^4 − 16 = 1 − 16 = −15\) |
| 0 | \(g(0) = (0)^4 − 16 = 0 − 16 = −16\) |
| 1 | \(g(1) = g(1) = (1)^4 − 16 = 1 − 16 = −15\) |
| 2 | \(g(2) = g(2) = (2)^4 − 16 = 16 − 16 = 0\) |
尽可能进行因子分解,然后通过创建解表来绘制函数的图形:
\(f(x) = x ^6 − 5x ^2 + 3\)
解决方案
这个多项式的度数为 6,很难分解。 创建解决方案表以绘制图表。
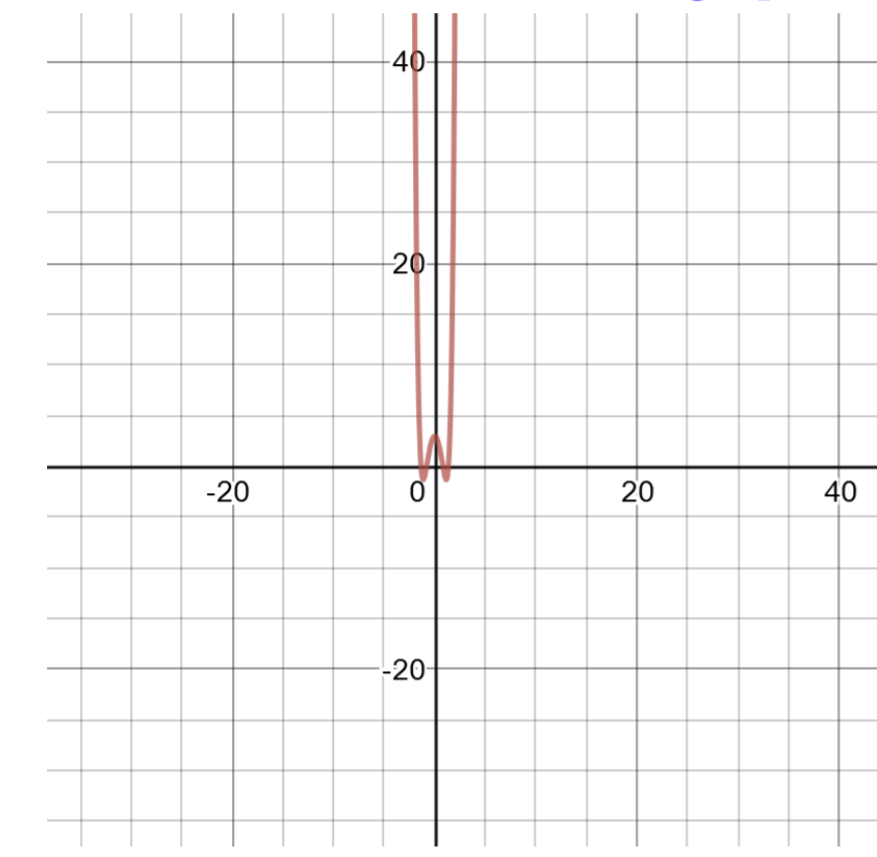
| 的解决方案表\(f(x) = x ^6 − 5x ^2 + 3\) | |
| \(x\) | \(f(x)\) |
| -2 | \(f(−2) = (−2)^6 − 5(−2)^2 + 3 = 47\) |
| -1 | \(f(−1) = (−1)^6 − 5(−1)^2 + 3 = −1\) |
| 0 | \(f(0) = (0)^6 − 5(0)^2 + 3 = 3\) |
| 1 | \(f(1) = (1)^6 − 5(1)^2 + 3 = −1\) |
| 2 | \(f(2) = (2)^6 − 5(2)^2 + 3 = 47\) |
- \(f(x) = x^3 − 27\)
- \(g(x) = 81x ^4 − 16\)
- \(h(x) = 2x ^5 − 4x ^2 − 6x + 3\)
- \(f(x) = 5x ^6 − 6x ^4 + 5\)
有理函数
有理函数是一种可以写成多项式商的函数。
\(f(x) = \dfrac{P (x) }{Q(x) }\),\(Q(x) \neq 0\)
其中\(P(x)\)和\(Q(x)\)是一个变量中的多项式\(x\)。 域是所有实数的集合,例如\(Q(x) \neq 0\)。
对于该函数,\(f(x) = \dfrac{9 }{x − 3}\):
- 绘制函数图表
- 计算\(x = 0\)和的函数\(x = 2\)
解决方案
注意这个函数的范围。 除以零是未定义的,因此必须从域中排除构成分母 0 的数字。
在这个问题中,\(x − 3\)是函数的分母。 设置\(x − 3 = 0\)并求解\(x\)。 如果\(x = 3\)除法未定义,则从函数的域中排除数字 3。 可以将其视为总是从所有实数开始,\((−\infty , \infty )\)然后删除会导致未定义除法的值。
此函数的域是\((−\infty , 3) \cup (3, \infty )\)。
有理函数通常会有渐近线,这条线连续接近给定曲线,但在任何有限距离内都不与之相遇。 你将在 Math 162 的 “曲线素描” 部分中学习渐近线。
这个函数的图表可以通过制作解决方案表来找到:

| 的解决方案表\(f(x) = \dfrac{9 }{x − 3}\) | 域名:\((−\infty , 3) \cup (3, \infty )\) |
| \(x\) | \(f(x)\) |
| -4 | \(-\dfrac{9}{7}\) |
| -3 | \(-\dfrac{3}{2}\) |
| -2 | \(-\dfrac{9}{5}\) |
| -1 | \(-\dfrac{9}{4}\) |
| 0 | \(-3\) |
| 1 | \(-\dfrac{9}{2}\) |
| 2 | \(-9\) |
对于这个函数,\(f(x) = \dfrac{100x}{ x^2 − 3x − 4}\)
- 绘制函数图表
- 计算\(x = −1\)和的函数\(x = 3\)
解决方案
注意这个函数的范围。 除以零是未定义的,因此必须从域中排除构成分母 0 的数字。
在这个问题中,\(x^2 − 3x − 4\)是函数的分母。 将二次表达式分解得到,\((x − 4)(x + 1)\)并将每个因子设置为等于零并求解\(x\):\(x − 4 = 0\), so\(x = 4\);\(x + 1 = 0\), so\(x = −1\)。 如果为\(x = 4\) or\(x = −1\),则除法未定义,因此从函数的域中排除数字 4 和 −1。 可以将其视为总是以所有实数开头,\((−\infty , \infty )\)然后删除会导致未定义除法的值。
此函数的域是\((−\infty , −1) \cup (−1, 4) \cup (4, \infty )\)。 这个函数的图表可以通过制作解决方案表来找到:
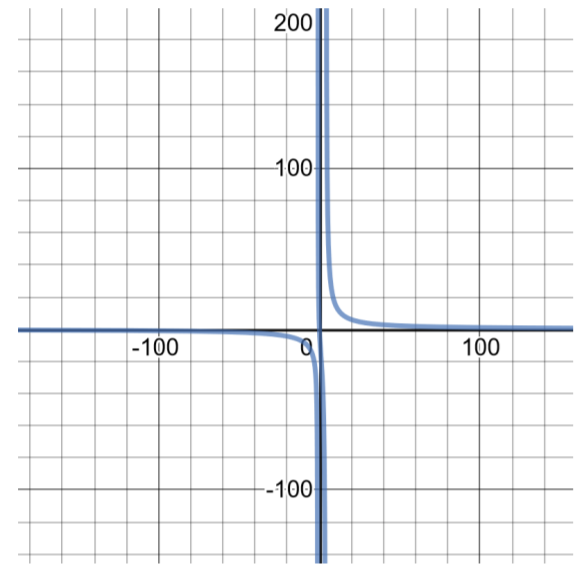
| 的解决方案表\(f(x) = \dfrac{100x}{ x^2 − 3x − 4}\) | 域名:\((−\infty , −1) \cup (−1, 4) \cup (4, \infty )\) |
| \(x\) | \(f(x)\) |
| -4 | −16.667 |
| -3 | −21.429 |
| -2 | −33.333 |
| -1 | 未定义 |
| 0 | 0 |
| 1 | −16.667 |
| 2 | −33.333 |
| 3 | -75 |
| 4 | 未定义 |
- \(f(x) = \dfrac{3x + 6 }{x − 1}\)
- \(f(x) = \dfrac{9 }{x^2 − 9}\)
- \(f(x) = \dfrac{x^ 2 − 4 }{x^2 − 4x}\)


