12.4: 几何序列和序列
- Page ID
- 203856
在本节结束时,您将能够:
- 确定序列是否为几何序列
- 找出几何序列的通用项(\(n\)第 1 项)
- 求出几何序列首\(n\)项的总和
- 求无限几何序列的总和
- 在现实世界中应用几何序列和序列
在开始之前,请参加这个准备测验。
- 简化:\(\frac{24}{32}\)。
如果你错过了这个问题,请查看示例 1.24。 - 评估:a.\(3^{4}\) b\(\left(\frac{1}{2}\right)^{4}\).
如果你错过了这个问题,请查看示例 1.19。 - 如果\(f(x)=4 \cdot 3^{x}\),找到 a.\(f(1)\) b.\(f(2)\) c\(f(3)\).
如果你错过了这个问题,请查看示例 3.49。
确定序列是否为几何序列
我们现在准备研究第二种特殊类型的序列,即几何序列。
如果连续项之间的比率始终相同,则该序列称为几何序列。 几何序列中连续项之间的比率为\(r\)常用比率,其中大\(n\)于或等于两项。
几何序列是连续项之间的比率始终相同的序列。
连续项之间的比率是常\(r\)用比率。\(\frac{a_{n}}{a_{n-1}}\) \(n\)大于或等于二。
以这些序列为例。
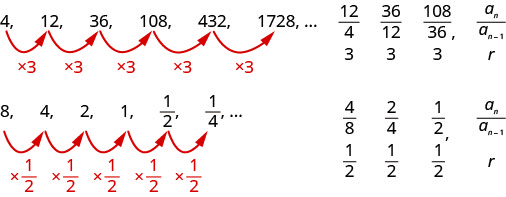
确定每个序列是否为几何序列。 如果是,请指明常用比率。
- \(4,8,16,32,64,128, \dots\)
- \(-2,6,-12,36,-72,216, \dots\)
- \(27,9,3,1, \frac{1}{3}, \frac{1}{9}, \ldots\)
解决方案:
为了确定序列是否为几何序列,我们找到了所示连续项的比率。
a. 找出连续术语的比率
\(\begin{aligned} 4, \quad& \:8, \quad 16, \quad 32, \quad 64, \quad 128, \dots \\ &\frac{8}{4} \quad\frac{16}{8}\quad\frac{32}{16}\quad\frac{64}{32}\quad\frac{128}{64} \\ &\:2 \quad\:\:\: 2 \quad\quad2\quad\quad2\quad\quad2 \end{aligned}\)
该序列是几何的。 常见的口粮是\(r=2\)。
b. 找出连续术语的比率
\(\begin{aligned}-\:2,\quad &\:\:\:6,\quad -12,\quad 36,\quad \:-72\quad \:\:216,\dots \\ & \frac{6}{-2}\quad\frac{-12}{6}\quad\frac{36}{-12}\quad\frac{-72}{36}\quad\frac{216}{-72} \\ & -3\quad -2\quad\:\: -3\quad \:\:\:-2\quad \:\:-3 \end{aligned}\)
该序列不是几何序列。 没有共同的比例。
c. 求出连续项的比率
\(\begin{aligned}27,\quad &\:\:9,\quad 3,\quad 1,\quad \frac{1}{3},\quad \frac{1}{9}, \ldots\\ & \frac{9}{27}\quad\frac{3}{9}\quad\frac{1}{3}\quad\frac{\frac{1}{3}}{1}\quad\frac{\frac{1}{9}}{\frac{1}{3}}\\ &\frac{1}{3}\quad\;\:\frac{1}{3}\quad\frac{1}{3}\quad\:\frac{1}{3}\quad\:\frac{1}{3}\end{aligned}\)
该序列是几何的。 常见的比率是\(r=\frac{1}{3}\)。
确定每个序列是否为几何序列。 如果是,请指明通用比率。
- \(7,21,63,189,567,1,701, \dots\)
- \(64,16,4,1, \frac{1}{4}, \frac{1}{16}, \dots\)
- \(2,4,12,48,240,1,440, \dots\)
- 回答
-
- 该序列是几何序列,比例相同\(r=3\)。
- 该序列是几何序列,比例相同\(d=\frac{1}{4}\)。
- 该序列不是几何序列。 没有共同的比例。
确定每个序列是否为几何序列。 如果是,请指明通用比率。
- \(-150,-30,-15,-5,-\frac{5}{2}, 0, \dots\)
- \(5,10,20,40,80,160, \dots\)
- \(8,4,2,1, \frac{1}{2}, \frac{1}{4}, \ldots\)
- 回答
-
- 该序列不是几何序列。 没有共同的比例。
- 该序列是几何序列,比例相同\(r=2\)。
- 该序列是几何序列,比例相同\(r=\frac{1}{2}\)。
如果我们知道第一个项和常用比率\(r\),我们可以列出序列中有限数量的项。\(a_{1}\)
写下序列的前五个项,其中第一个项是\(3\),常用比率为\(r=−2\)。
解决方案:
我们从第一个项开始,然后将其乘以常用比率。 然后我们将该结果乘以常用比率得出下一个项,依此类推。
\(\begin{array}{cccc}{a_{1}} & {a_{2}} & {a_{3}} & {a_{4}} & {a_{5}} \\ {3} & {3 \cdot(-2)} & {-6 \cdot(-2)} & {12 \cdot(-2)} & {-24 \cdot(-2)} \\& {-6} & {12} & {-24} & {48}\end{array}\)
答案:
顺序是\(3,-6,12,-24,48, \dots\)
写下序列的前五个项,其中第一个项是\(7\),常用比率为\(r=−3\)。
- 回答
-
\(7,-21,63,-189,567\)
写下序列的前五个项,其中第一个项是\(6\),常用比率为\(r=−4\)。
- 回答
-
\(6,-24,96,-384,1536\)
找出几何序列的通用项(\(n\)第 4 项)
就像我们找到了序列的通用项和算术序列的公式一样,我们也可以找到几何序列的通用项的公式。
让我们写下序列的前几个项,其中第一个项是\(a_{1}\),常用比率是\(r\)。 然后我们将寻找一种图案。
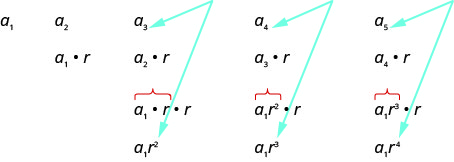
当我们在上面五个术语中寻找模式时,我们发现每个术语都以开头\(a_{1}\)。
第一个项\(a_{1}\)不乘以任一\(r\)。 在第二个项中\(a_{1}\),将乘以\(r\)。 在第三项中\(a_{1}\),将乘以\(r\)两倍(\(r⋅r\)或\(r^{2}\))。 在第四项中\(a_{1}\),将乘以\(r\)三倍(\(r⋅r⋅r\)或\(r^{3}\)),在第五项中\(a_{1}\),将乘以\(r\)四倍。 在每个项中,次数乘以\(a_{1}\)比该\(r\)项的次数少一。 这使我们得出以下几点
\(a_{n}=a_{1} r^{n-1}\)
具有第一项\(a_{1}\)和常用比率的几何序列的总\(r\)项为
\(a_{n}=a_{1} r^{n-1}\)
我们将在下一个示例中使用此公式来查找序列的第十四项。
找出序列的第十四项,其中第一个项为\(64\),常用比率为\(r=\frac{1}{2}\)。
解决方案:
\(a_{n}=a_{1} r^{n-1}\)
要找到第十四个术语\(a_{14}\),请使用带有 and 的\(a_{1}=64\)公式\(r=\frac{1}{2}\)。
\(a_{14}=64\left(\frac{1}{2}\right)^{14-1}\)
在值中替换。
\(a_{14}=64\left(\frac{1}{2}\right)^{13}\)
简化。
\(a_{14}=\frac{1}{128}\)
找出序列的第十三项,其中第一个项为\(81\),常用比率为\(r=\frac{1}{3}\)。
- 回答
-
\(\frac{1}{6,561}\)
找出序列的第十二项,其中第一个项为\(256\),常用比率为\(r=\frac{1}{4}\)。
- 回答
-
\(\frac{1}{16,384}\)
有时我们不知道通用比率,在找到所要求的术语之前,我们必须使用给定的信息来找到它。
找到序列的第十二项\(3, 6, 12, 24, 48, 96, …\)找到该序列的通用项。
解决方案:
要找到第十二项,我们使用公式\(a_{n}=a_{1} r^{n-1}\),因此我们需要首先确定\(a_{1}\)和通用比率\(r\)。
第一个学期是三个。
\(3,6,12,24,48,96, \dots\)
\(a_{1}=3\)
找到常用比率。
\(\begin{array}{l}{\frac{6}{3} \quad \frac{12}{6} \quad \frac{24}{12} \quad \frac{48}{24} \quad \frac{96}{48}} \\ {2 \:\:\:\quad 2 \quad \:\:2 \quad\:\:\: 2 \:\:\quad \:2} \\ {\text { The common ratio is } r=2}\end{array}\)
要找到第十二个项\(a_{12}\),请使用带有 and\(a_{1}=3\) 的公式\(r=2\)。
\(a_{n}=a_{1} r^{n-1}\)
在值中替换。
\(a_{12}=3 \cdot 2^{12-1}\)
简化。
\(a_{12}=3 \cdot 2^{11}\)
\(a_{12}=6,144\)
找到通用术语。 我们使用带有 and 的\(a_{1}=3\)公式\(r=2\)。
\(a_{n}=a_{1} r^{n-1}\)
\(a_{n}=3(2)^{n-1}\)
找到序列的第九项\(6, 18, 54, 162, 486, 1,458, … \)然后找到该序列的通用项。
- 回答
-
\(a_{9}=39,366 .\)一般术语是\(a_{n}=6(3)^{n-1}\)。
找到序列的第十一个项\(7, 14, 28, 56, 112, 224, …\)然后找到该序列的通用项。
- 回答
-
\(a_{11}=7,168 .\)一般术语是\(a_{n}=7(2)^{n-1}\)。
求几何序列首\(n\)项之和
我们找到了通用序列和算术序列的总和。 现在,我们将对几何序列做同样的事情。 几何序列的第一个\(n\)项的总和写为\(S_{n}=a_{1}+a_{2}+a_{3}+\ldots+a_{n}\)。\(S_{n}\) 我们可以从第一个项开始写出这个总和\(a_{1}\),然后继续乘\(r\)以得出下一个项:
\(S_{n}=a_{1}+a_{1} r+a_{1} r^{2}+\ldots+a_{1} r^{n-1}\)
让我们也将方程的两边乘以\(r\)。
\(r S_{n}=a_{1} r+a_{1} r^{2}+a_{1} r^{3}+\ldots+a_{1} r^{n}\)
接下来,我们减去这些方程。 我们将看到,当我们减去时,除顶部方程的第一项和底部方程的最后一项外,其他所有项都减去为零。
\(\begin{aligned} S_{n}&= a_{1}+a_{1} r+a_{1} r^{2}+a_{1} r^{3}+\ldots+a_{1} r^{n-1} \\ r S_{n} &= a_{1} r+a_{1} r^{2}+a_{1} r^{3}+\ldots+a_{1} r^{n-1}+a_{1} r^{n}\\\hline S_{n}-r S_{n} &= a_{1} -a_{1}r^{n} \end{aligned}\)
我们将双方都考虑在内。
\(S_{n}(1-r)=a_{1}\left(1-r^{n}\right)\)
要获得的公式\(S_{n}\),请将两边除以\((1-r)\)。
\(S_{n}=\frac{a_{1}\left(1-r^{n}\right)}{1-r}\)
几何序列的第一个\(n\)项的总和为\(S_{n}\)
\(S_{n}=\frac{a_{1}\left(1-r^{n}\right)}{1-r}\)
其中\(a_{1}\)是第一个项,\(r\)是常用比率,\(r\)不等于一。
我们在下一个示例中应用这个公式,其中给出了序列的前几个项。 请注意,当常用比率大于 1 时,几何序列的总和通常会变得非常大。
求出几何序列首\(20\)项的总和\(7, 14, 28, 56, 112, 224, …\)
解决方案:
为了找到总和,我们将使用公式\(S_{n}=\frac{a_{1}\left(1-r^{n}\right)}{1-r}\)。 我们知道\(a_{1}=7\)\(r=2\),而且\(n=20\),
知道\(a_{1}=7, r=2\)\(n=20\),然后使用总和公式。
\(S_{n}=\frac{a_{1}\left(1-r^{n}\right)}{1-r}\)
在值中替换。
\(S_{20}=\frac{7\left(1-2^{20}\right)}{1-2}\)
简化。
\(S_{20}=7,340,025\)
求出几何序列首\(20\)项的总和\(3, 6, 12, 24, 48, 96, …\)
- 回答
-
\(3,145,725\)
求出几何序列首\(20\)项的总和\(6, 18, 54, 162, 486, 1,458, …\)
- 回答
-
\(10,460,353,200\)
在下一个示例中,我们以求和表示法给出了总和。 虽然添加所有项是可能的,但大多数情况下,最简单的方法是使用公式来求出第一个\(n\)项的总和。
要使用这个公式,我们需要\(r\)。 我们可以通过写出序列的前几个项并找到它们的比率来找到它。 另一种选择是认识到,在求和表示法中,序列是以形式书写的\(\sum_{i=1}^{k} a(r)^{i}\),其中\(r\)是常用比率。
找到总和:\(\sum_{i=1}^{15} 2(3)^{i}\).
解决方案:
为了找到总和,我们将使用公式\(S_{n}=\frac{a_{1}\left(1-r^{n}\right)}{1-r}\),该公式需要\(a_{1}\)和\(r\)。 我们将写出一些条款,以便我们获得所需的信息。
 |
|
| 写出前几个术语。 | 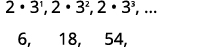 |
| 识别\(a_{1}\)。 |  |
| 找到常用比率。 |  |
| 知道\(a_{1}=6\)\(r=3\)、和\(n=15\),使用总和公式。 | 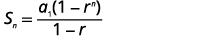 |
| 在值中替换。 | 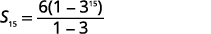 |
| 简化。 | 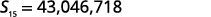 |
找到总和:\(\sum_{i=1}^{15} 6(2)^{i}\).
- 回答
-
\(393,204\)
找到总和:\(\sum_{i=1}^{10} 5(2)^{i}\).
- 回答
-
\(10,230\)
求无限几何序列的总和
如果我们取一个几何序列并将这些项相加,就会得到一个称为几何序列的总和。 无限几何序列是一个无限和,其第一个项是\(a_{1}\),常用比率是\(r\)写入的
\(a_{1}+a_{1} r+a_{1} r^{2}+\ldots+a_{1} r^{n-1}+\ldots\)
无限几何序列是一个无限和,其第一个项是\(a_{1}\),常用比率是\(r\)写入的
\(a_{1}+a_{1} r+a_{1} r^{2}+\ldots+a_{1} r^{n-1}+\dots\)
我们知道如何使用公式求出几何序列的第一个\(n\)项的总和\(S_{n}=\frac{a_{1}\left(1-r^{n}\right)}{1-r}\)。 但是我们如何找到无限和的总和呢?
让我们来看看无限几何系列\(3+6+12+24+48+96+….\)。 每个项越来越大,因此无限个项的总和越来越大是有道理的。 让我们来看一下本系列的部分总和。 我们看见\(a_{1}=3\)了\(r=2\)
\(\begin{array}{lll}{S_{n}=\frac{a_{1}\left(1-r^{n}\right)}{1-r}} & {S_{n}=\frac{a_{1}\left(1-r^{n}\right)}{1-r}} & {S_{n}=\frac{a_{1}(1-r^{n})}{1-r}}\\ {S_{10}=\frac{3\left(1-2^{10}\right)}{1-2}} & {S_{30}=\frac{3\left(1-2^{30}\right)}{1-2}} & {S_{50}=\frac{3\left(1-2^{50}\right)}{1-2}} \\ {S_{10}=3,069} & {S_{30}=3,221,225,469} & {S_{50}\approx 3.38 \times 10^{15}}\end{array}\)
\(n\)随着越来越大,总和越来越大。 当我们称该系列为\(|r|≥1\) divergent 时,情况确实如此。 什么时候我们找不到无限几何序列的总和\(|r|≥1\)。
让我们来看一个无限的几何序列,其常用比率小于一的分数
\(\frac{1}{2}+\frac{1}{4}+\frac{1}{8}+\frac{1}{16}+\frac{1}{32}+\frac{1}{64}+\ldots\)。 在这里,术语越来越小,\(n\)越来越大。 让我们来看看这个系列的几个有限和。 我们看到\(a_{1}=\frac{1}{2}\)了\(r=\frac{1}{2}\)。
\(\begin{array}{lll}{S_{n}=\frac{a_{1}\left(1-r^{n}\right)}{1-r}} & {S_{n}=\frac{a_{1}\left(1-r^{n}\right)}{1-r}} & {S_{n}=\frac{a_{1}(1-r^{n})}{1-r}}\\ {S_{10}=\frac{\frac{1}{2}\left(1-\frac{1}{2}^{10}\right)}{1-\frac{1}{2}}} & {S_{20}=\frac{\frac{1}{2}\left(1-\frac{1}{2}^{20}\right)}{1-\frac{1}{2}}} & {S_{30}=\frac{\frac{1}{2}\left(1-\frac{1}{2}^{30}\right)}{1-\frac{1}{2}}} \\ {S_{10}\approx 0.9990234375} & {S_{20}\approx 0.9999990463} & {S_{30}\approx 0.9999999991}\end{array}\)
请注意,总和越来越大,但也越来越接近一。 当时\(|r|<1\),表达式\(r^{n}\)变得越来越小。 在这种情况下,我们称该系列为收敛。 当\(n\)接近无穷大时,(\(r^{n}\)变得无限大)越来越接近零。 在我们的总和公式中,我们可以将\(r^{n}\)替换为零,\(S\)然后得到一个无限几何序列的总和公式\(|r|<1\)。
\(\begin{aligned} S_{n} &=\frac{a_{1}\left(1-r^{n}\right)}{1-r} \\ S &=\frac{a_{1}(1-0)}{1-r} \\ S &=\frac{a_{1}}{1-r} \end{aligned}\)
这个公式给出了无限几何序列的总和。 请注意,\(S\)没有像我们\(n\)\(S_{n}\)一样的下标,因为我们没有添加有限数量的项。
对于第一个项为常用比率的无限几何序列\(r\),\(a_{1}\)
如果\(|r|<1\),总和为
\(S=\frac{a_{1}}{1-r}\)
如果\(|r|≥1\),则无限几何序列没有总和。 我们说这个系列有分歧。
求无限几何序列的总和\(54+18+6+2+\frac{2}{3}+\frac{2}{9}+\ldots\)
解决方案:
要找到总和,我们首先必须验证公用比率,\(|r|<1\)然后才能使用总和公式\(S=\frac{a_{1}}{1-r}\)。
找到常用比率。
\(\begin{array}{ll}{r=\frac{18}{54}} & {r=\frac{6}{18} \dots} \\ {r=\frac{1}{3}} & {r=\frac{1}{3} \quad|r|<1}\end{array}\)
识别\(a_{1}\)。
\(a_{1}=54\)
知道\(a_{1}=54, r=\frac{1}{3}\)了,使用总和公式。
\(S=\frac{a_{1}}{1-r}\)
在值中替换。
\(S=\frac{54}{1-\frac{1}{3}}\)
简化。
\(S=81\)
答案:
\(S=80\)
求无限几何序列的总和\(48+24+12+6+3+\frac{3}{2}+\dots\)
- 回答
-
\(96\)
求无限几何序列的总和\(64+16+4+1+\frac{1}{4}+\frac{1}{16}+\dots\)
- 回答
-
\(\frac{256}{3}\)
无限几何序列的一个有趣用法是将重复的十进制写成分数。
将重复的十进制写\(0.5\)成分数。
解决方案:
重写\(0.5\)显示的重复五个。 使用位值将其重写为总和。 这是一个无限的几何系列。
0.555555555555\(\ldots\)
\(0.5+0.05+0.005+0.0005+\dots\)
找到常用比率。
\(\begin{array}{ll}{r=\frac{0.05}{0.5}} & {r=\frac{0.005}{0.05} \dots} \\ {r=0.1} & {r=0.1 \quad|r|<1}\end{array}\)
识别\(a_{1}\)
\(a_{1}=0.5\)
知道\(a_{1}=0.5 ,r=0.1\)了,使用总和公式。
\(S=\frac{a_{1}}{1-r}\)
在值中替换。
\(S=\frac{0.5}{1-0.1}\)
简化。
\(S=\frac{0.5}{0.9}\)
将分子和分母乘以\(10\)。
\(S=\frac{5}{9}\)
我们被要求找到分数形式。
\(0.5 = \frac{5}{9}\)
将重复的十进制写\(0.4\)成分数。
- 回答
-
\(\frac{4}{9}\)
将重复的十进制写\(0.8\)成分数。
- 回答
-
\(\frac{8}{9}\)
在现实世界中应用几何序列和序列
几何序列的一个应用与消费者支出有关。 如果向每个家庭提供退税,则对经济的影响是个人退税金额的许多倍。
政府已决定向每个家庭提供美元退\(1,000\)税,以刺激经济。 政府统计数据显示,每个家庭将把折扣的\(80\)百分比花在商品和服务上。 然后,从该\(80\)百分比中受益的企业和个人将花费他们收到的金额的\(80\)百分比,依此类推。 结果称为乘数效应。 回扣对经济的总体影响是什么?
解决方案:
每当资金流入经济时,其中的\(80\)百分比都花在了经济中,然后花在经济中。 再说一遍,这笔钱的\(80\)百分比又花在了经济上。 这种情况仍在继续,因此我们得出了无限的几何序列。
\(1000+1000(0.8)+1000(0.8)^{2}+\ldots\)
这里的第一个学期是\(1,000, a_{1}=1000\)。 常见的比率是\(0.8, r=0.8\)。 从那以后我们可以评估这个总和\(0.8<1\)。 我们使用公式计算无限几何序列的总和。
\(S=\frac{a_{1}}{1-r}\)
在值中替换,\(a_{1}=1,000\)和\(r=0.8\)。
\(S=\frac{1,000}{1-0.8}\)
评估。
\(S=5,000\)
答案:
每个家庭\(1,000\)获得的美元所产生的总影响将是经济的美元\(5,000\)增长。
如果每个家庭将退税的\(90\)百分比花在商品和服务上,那么政府为刺激经济而向每个家庭提供美元的\(1,000\)退税对经济的总体影响是多少?
- 回答
-
$\(10,000\)
如果每个家庭将退税的\(85\)百分比花在商品和服务上,那么政府为刺激经济而向每个家庭提供美元的\(500\)退税对经济的总体影响是多少?
- 回答
-
$\(3,333.33\)
我们已经研究了一个复利公式\(P\),即\(t\)多年来本金是按利\(r\)率投资的。 新的余额是指每年\(n\)多次复利\(A=P\left(1+\frac{r}{n}\right)^{n t}\)的时候。\(A\) 此公式适用于预先一次性投资并告诉我们一定时间段后的价值。
年金是一系列相等的定期存款的投资。 我们将研究在存款时支付利息的年金。 当我们制定年金价值的公式时,我们将放弃\(n=1\)。 这意味着每年有一笔存款。
\(\begin{aligned} &A =P\left(1+\frac{r}{n}\right)^{n t} \\ \text { Let } n=1 .\quad & A=P\left(1+\frac{r}{1}\right)^{1 t} \\ \text { Simplify. }\quad & A=P(1+r)^{t} \end{aligned}\)
假设在每年年底投资\(P\)美元。 一年后,这笔存款价值\(P(1+r)^{1}\)美元,又过了一年,它价值了\(P(1+r)^{2}\)美元。 \(t\)多年后,它将物有所\(P(1+r)^{t}\)值。
| 年底\(1\) | 年底\(2\) | 年底\(3\) | |
|---|---|---|---|
| 首次存款\(P\) @ 年底\(1\) | \ (1\)” >\(P\) | \ (2\) “>\(1\) 一年后的金额\(P(1+r)^{1}\) | \ (3\) “>数\(2\)年后的金额\(P(1+r)^{2}\) |
| \(2\)nd 存款\(P\) @ 年底\(2\) | \ (1\)” > | \ (2\)” >\(P\) | \ (3\) “>\(1\) 一年后的金额\(P(1+r)^{1}\) |
| \(3\)第三笔存款\(P\) @ 年底\(3\) | \ (1\)” > | \ (2\)” > | \ (3\)” >\(P\) |
三年后,年金的价值为
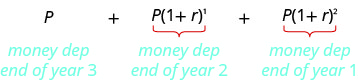
这是几何序列项的总和,其中第一个项为\(P\),常用比率为\(1+r\)。 我们将这些值替换为总和公式。 小心,我们有两种不同的用法\(r\)。 总和公式\(r\)中的是序列的常用比率。 在这种情况下,这就是利率\(1+r\)在哪里\(r\)。
\(\begin{aligned} &S_{t} =\frac{a_{1}\left(1-r^{t}\right)}{1-r} \\ \text { Substitute in the values. }\quad & S_{t}=\frac{P\left(1-(1+r)^{t}\right)}{1-(1+r)} \\ \text { Simplify. }\quad & S_{t} =\frac{P\left(1-(1+r)^{t}\right)}{-r} \\ &S_{t} =\frac{P\left((1+r)^{t}-1\right)}{r} \end{aligned}\)
请记住,我们的前提是每年年底存入一笔存款。
我们可以根据每年的\(n\)存款调整这个公式,利息每年按复利\(n\)次数计算。
对于在复利\(P\)期结束时投资的本金,利率为每年复利\(n\)次数,\(t\)多年后的新余额为\(r\)\(A\)
\(A_{t}=\frac{P\left(\left(1+\frac{r}{n}\right)^{n t}-1\right)}{\frac{r}{n}}\)
新父母决定\(100\)每月投资美元为宝贝女儿支付年金。 该账户每年将支付\(5\)百分比的利息,按月复利。 孩子十八岁生日时账户里会有多少钱?
解决方案:
要找到年金公式\(A_{t}=\frac{P\left(\left(1+\frac{r}{n}\right)^{n t}-1\right)}{\frac{r}{n}}\),我们需要确定\(P, r, n\)和\(t\)。
确定\(P\)每月的投资金额。
\(P=100\)
以十进制形式标识\(r\)年利率。
\(r=0.05\)
确定\(n\)每年的存款次数和复利的利息。
\(n=12\)
确定\(t\)年数。
\(t=18\)
知道\(P=100, r=0.05, n=12\)并\(t=18\)使用总和公式。
\(A_{t}=\frac{P\left(\left(1+\frac{r}{n}\right)^{n t}-1\right)}{\frac{r}{n}}\)
在值中替换。
\(A_{t}=\frac{100\left(\left(1+\frac{0.05}{12}\right)^{12.18}-1\right)}{\frac{0.05}{12}}\)
使用计算器进行评估。 请务必根据需要使用括号。
\(A_{t}=34.920 .20\)
答案:
孩子会有 $\(34,920.20\)
新祖父母决定\(200\)每月投资美元为孙子支付年金。 该账户每年将支付\(5\)百分比的利息,按月复利。 孩子二十一岁生日时账户里会有多少钱?
- 回答
-
$\(88,868.36\)
阿图罗(Arturo)大学毕业后刚找到第一份全职工作\(27\). 他决定\(200\)每月投资美元购买IRA(年金)。 年金的利息为\(8\) %,按月复利。 当阿图罗六十七岁生日退休时,他的账户里会有多少钱?
- 回答
-
$\(698,201.57\)
访问这些在线资源以获取更多指导和序列练习。
关键概念
- 几何序列的通用项(\(n\)第 1 项):具有第一项\(a_{1}\)和常用比率的几何序列的总\(r\)项为
\(a_{n}=a_{1} r^{n-1}\)
- 几何@@ 序列首\(n\)项之和:几何序列\(n\)项的总和为\(S_{n}\)
\(S_{n}=\frac{a_{1}\left(1-r^{n}\right)}{1-r}\)
其中\(a_{1}\)是第一个项,\(r\)是常用比率。 Infinite Geometry Series:无限几何序列是一个无限和,其第一个项是\(a_{1}\),常用比率是\(r\)写入的\(a_{1}+a_{1} r+a_{1} r^{2}+\ldots+a_{1} r^{n-1}+\ldots\)
- 无限几何序列的总和:对于第一个项为常用比率的无限几何序列\(r\)
\(|r|<1\),总\(a_{1}\)和为
\(S=\frac{a_{1}}{1-r}\)
我们说这个系列趋于一致。
如果\(|r|≥1\),则无限几何序列没有总和。 我们说这个系列有分歧。
- 年利息复合\(n\)倍数的年金价值:对于本金\(P\),在复利期结束时投资,利率为每年复利\(n\)次数\(A\),之后的新余额\(r\)\(t\)年份,是
\(A_{t}=\frac{P\left(\left(1+\frac{r}{n}\right)^{n t}-1\right)}{\frac{r}{n}}\)
词汇表
- 年金
- 年金是一系列相等的定期存款的投资。
- 普通比率
- 几何序列中连续项之间的比率是\(r\)常用比率,其中\(r\)大于或等于两项。\(\frac{a_{n}}{a_{n-1}}\)
- 几何序列
- 几何序列是连续项之间的比率始终相同的序列
- 无限几何系列
- 无限几何序列是无限和的无限几何序列。


